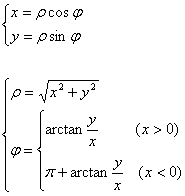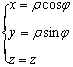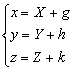Chapter 7 Analytical and Differential Geometry
Analytical geometry is to use algebraic methods to study the properties of geometric figures. Its main research objects are straight lines, planes, quadratic curves and quadric surfaces . Differential geometry is to use infinitesimal analysis methods to study the properties of geometric figures, and its main research objects are curves. with surfaces .
Everything in this chapter is discussed only in Euclidean ( excluding affine and projective ) spaces .
There are eleven sections in the whole chapter . The first six sections belong to analytic geometry, which describe the coordinate system, coordinate transformation and basic calculation formulas of plane and space; , lists the basic elements, standard equations, main properties and calculation formulas of various types of quadratic curves and quadric surfaces in detail . General properties of subsurfaces, and use invariants to write standard equations and shape determinations .
The content of the last five sections belongs to differential geometry. Regarding the theory of curves, the following are given here: the Shelley - Fleiner formula and the fundamental theorem of plane curves and space curves, as well as the concepts and calculation formulas of their curvature and torsion; equidistant lines , the definitions and equations of involutes, involutes and envelopes, and the equations, graphics and various characteristics of important plane curves and some special space curves are collected in more detail . Regarding the theory of surfaces, only a few special ones are described here . Equations, graphics and properties of surfaces, and basic elements of surfaces ( equations and formulas such as arc length, area, angle, tangent, normal surface, etc. ) , basic forms, basic equations, basic theorems, curvature lines, asymptotic curves, Conjugate curve, geodesic and normal curvature, geodesic curvature, total curvature, mean curvature, Bonne formula, etc.
For the concepts, operations and formulas related to vectors in this chapter, please refer to Chapter 8 .
§ 1 Coordinate system and coordinate transformation
1. Plane coordinate system and its transformation table
|
Coordinate Systems and Graphics |
Formula and Explanation |
|||
|
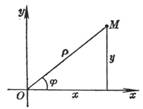
[ Cartesian Cartesian Coordinate System ]
|
Ox is the horizontal axis, Oy is the vertical axis M(x , y) x is the abscissa y is the ordinate I , II , III , and IV are four quadrants, and the symbols of the coordinates x and y of the points in each quadrant are |
|||
|
|
quadrant |
I II III IV |
|
|
|
x y |
+ - - + + + - - |
|||
|
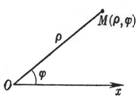
[ Polar Coordinate System ]
|
O is the pole, Ox is the polar axis M ( r , j ) r is the vector radius (0 £ r < ¥ ) j is the polar angle ( - ¥ < j < ¥ ) j starts from the polar axis, turning counterclockwise is positive, and turning clockwise is negative
|
|||
|
Coordinate Systems and Graphics |
Formula and Explanation |
|||
|
[ Exchange of Cartesian Coordinate System and Polar Coordinate System ]
|
|
|||
|
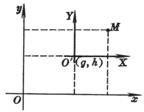
[ Translation of the coordinate axis ]
|
Here x , y represent the old coordinates, X , Y represent the new coordinates, g , h are the coordinates of the origin of the new coordinate system O ¢ in the old coordinate system
|
|||
|
[ Rotation of the coordinate axis ]
|
a is the angle that the coordinate axis rotates around the origin Any coordinate transformation can be decomposed into two parts: the translation of the coordinate axis and the rotation of the coordinate axis
|
|||
2. Space coordinate system and its transformation table
|
Coordinate Systems and Graphics |
Formula and Explanation |
|||||
|
[ Cartesian Cartesian Coordinate System ]
(a) Right-handed ( b ) Left-handed
( c ) |
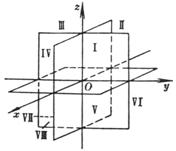
Ox is the horizontal axis, Oy is the vertical axis, Oz is the vertical axis M ( x , y , z ) x is the abscissa y is the ordinate z is the vertical coordinate I to VIII are eight hexagram limits, and the symbols of the coordinates x , y , and z of points in each hexagram limit are : |
|||||
|
|
Gua limit |
I II III IV V VI VII VIII |
||||
|
x y z |
+ - - + + - - + + + - - + + - - + + + + - - - - |
|||||
|
|
||||||
|
Coordinate Systems and Graphics |
Formula and Explanation |
|||||
|
[ Cylindrical coordinate system ]
|
r , j are the polar coordinates of the projection of point M on the Oxy plane, and z is the distance from point M to the Oxy plane . Here 0 £ r < ¥ - ¥ < j < ¥ - ¥ < z < ¥ |
|||||
|
[ Spherical Coordinate System ( Polar Coordinate System )]
|
r is the length of the vector radius ( OM ) , j is the longitude, and q is the latitude ( or polar distance angle ) here 0 £ r < ¥ - ¥ < j < ¥ 0 £ q £ p
|
|||||
|
[ Exchange of Cylindrical Coordinates and Cartesian Coordinates ]
|
|
|||||
|
[ Exchange of spherical coordinates and Cartesian coordinates ]
|
|
|||||
|
[ Translation of the coordinate axis ]
|
where x , y , z are the old coordinates; X , Y , Z are the new coordinates; g , h , k are the coordinates of the origin of the new coordinate system O ¢ in the old coordinate system |
|||||
|
[ Rotation of the coordinate axis ]
|
The following table gives the direction cosines of the new axes OX , OY , OZ when |
|||||
|
|
new axis |
Direction cosine ( see § 4) |
|
|||
|
OX OY OZ |
l 1 m 1 n 1 l 2 m 2 n 2 l 3 m 3 n 3 |
|||||
|
then there are
|
||||||
[ Eulerian angles ] The position of the new coordinate axis can also be determined by three so-called Euler angles ( see above ) :
(i) Nutation angle q is the positive angle between OZ and Oz (0 £ q < p ).
(ii) The precession angle y is the angle between OA and Ox (0 £ y < 2 p ) , OA is the intersection of the OXY and Oxy planes, facing the positive direction of the Oz axis, y is counterclockwise from the Ox axis Start calculating .
(iii) The rotation angle j is the angle between OA and OX (0 £ j < 2 p ) , facing the positive direction of the OZ axis, j is calculated from the OX axis in the counterclockwise direction
if
c 1 = c os θ , c 2 = c os y , c 3 = c os j
s 1 =sin θ , s 2 =sin y , s 3 =sin j
but
l 1 = c 2 c 3 - c 1 s 2 s 3 , m 1 = s 2 c 3 + c 1 c 2 s 3 , n 1 = s 1 s 3
l 2 = - c 2 s 3 – c 1 s 2 c 3 , m 2 = - s 2 s 3 + c 1 c 2 c 3 , n 2 = s 1 c 3
l 3 = s 1 s 2 , m 3 = - s 1 c 2 , n 3 = c 1
Transform determinant Δ = 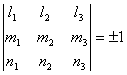
When the right-handed system becomes the right-handed system ( or the left-handed system becomes the left-handed system ) , Δ =1. When the right-handed system becomes the left-handed system ( or the left-handed system becomes the left-handed system)
is right-handed system ) , Δ = - 1 .