三、电磁学

 

【电磁学】电学与磁学的统称，是物理学中的一个重要部门。研究电磁现象的规律和应用的科学。研究对象包括静电现象、磁现象、电流现象、电磁感应、电磁辐射和电磁场等。磁现象和电现象本质上是紧密联系在一起的，变化的磁场能够激发电场，变化的电场也能够激发磁场。它是电工学和无线电电子学的基础。

【电】人类在很早以前就知道琥珀摩擦后，具有吸引稻草片或羽毛屑等轻小物体的特性。物体具有吸引其它物体的这种性质叫做“物体带电”或称“物体有了电荷”，并认识到电有正负两种；同性相斥，异性相吸。当时并不知道电是实物的一种属性，认为电是附着在物体上的，因而把它称为电荷，并把具有这种斥力或引力的物体称为带电体。习惯上经常也把带电体本身简称为电荷。近代科学证明；构成实物的许多基本粒子都是带电的，如质子带正电，电子带负电，质子和电子具有的绝对电量是相等的，是电量的最小单位。一切物质都是由大量原子构成，原子又是由带正电的原子核和带负电的电于组成。通常，同一个原子中的正负电量相等，因此在正常情况下表现为中性的或不带电的。若由于某些原因（如摩擦、受热或化学变化等）而失去一部分电子，就带正电，若得到额外的电子时，就带负电。用丝绸摩擦玻璃棒，玻璃棒就失去电子而带正电，丝绸得到电子而带负电。

【摩擦起电】两种不同物体相互摩擦后，分别带有正电和负电的现象。其原因是，当物体相互摩擦时电子由一个物体转移到另一个物体上，因此原来两个不带电的物体因摩擦而带电，它们所带的电量数值上相等，电性上相异。

【静电感应】在带电体附近的导体，受带电体的影响在其表面的不同部分出现正负电荷的现象叫作“静电感应”。因为，在带电体电场作用下，导体中的自由电子进行重新分布，造成导体内的电场随之而变化，直到抵消了带电体电场的影响，使它的强度减小到零为止。结果靠近带电体的一端出现与带电体异号的电荷，另一端出现与带电体同号的电荷。如果导体原来不带电，则两端带电数量相等；如果导体原来带电，则两端电量的代数和应与导体原带电量相等。在带电体附近的导体因静电感应而表面出现电荷的现象称为“感生电荷”。

【电荷守恒定律】在任何物理过程中，各个物体的电荷可以改变，但参于这一物理过程的所有物体电荷的代数和是守恒的，也就是说：电荷既不能创造，也不能被消灭，它们只能从一个物体转移到另一个物体，或者从物体的一部分转移到另一部分。例如中性物体互相摩擦而带电时，两物体带电量的代数和仍然是零。这就是电荷守恒定律。

【库仑定律】表述两个静止点电荷间相互作用力的定律。是法国物理学家库仑于1785年发现的。概述为：在真空中两个静止点电荷之间的相互作用力F的大小和它们的电量Q1和Q2和乘积成正比，和它们之间的距离r的平方成反比；作用力的方向沿着它们的连线，同号电荷相斥，

静电单位制中为1，式中F的单位是达因，Q的单位是静电单位制的电

式中F的单位是牛顿，Q的单位是库仑，r的单位是米，这时比例系数K等于9×109牛顿·米2/库仑2。为了简化电学中许多常用公式，往往将

【库仑】（Charles－Augustin de Coulomb，1736～1806）法国工程师、物理学家。1736年6月14日生于法国昂古莱姆。他曾在美西也尔工程学校读书，这是一座新型的讲授理论和应用知识的学校。离开学校后，进入皇家军事工程队当工程师。他在西印狄兹工作了9年，因病而回到法国。法国大革命时期，库仑辞去一切职务，到布卢瓦致力于科学研究。法皇执政统治时期，他回到巴黎，成为新建研究院成员。库仑在1773年发表有关材料强度的论文，他提出使各种物体经受应力和应变直到它们的折断点，然后根据这些资料就能计算出物体上应力和应变的分布情况。这种方法沿用至今，是结构工程的理论基础。1777年库仑开始研究静电和磁力问题。当时法国科学院悬赏，征求改良航海指南针中的磁针问题。库仑认为磁针支架在轴上，必然会带来摩擦，要改良磁针的工作，必须从这一根本问题入手，他提出用细头发丝或丝线悬挂磁针。他又发现线扭转时的扭力和磁针转过的角度成比例关系，从而可利用这种装置算出静电力或磁力的大小。这导致他发明定量扭秤。扭秤能以极高的精度测出非常小的力。1779年库仑分析摩擦力，并提出有关润滑剂的科学理论。他还设计出水下作业法，类似于现代的沉箱。1785～1789年，库仑用扭秤测量静电力和磁力，导出了有名的库仑定律。1806年8月23日库仑在巴黎逝世。电荷的单位库仑，就是以他的姓氏命名的。

【点电荷】点电荷并不是指带电体非常小的电荷实体，而是在所讨论的问题中可以不考虑其大小和分布状况的带电体。例如，当带电体的线度在所讨论的问题中远小于其他距离和长度时。这时的电荷分布也可看作为点电荷。点电荷只是一个为讨论问题方便而引入的理想概念，这一点与研究力学时引入质点的概念相似。

【电介质】不导电的物质称为“电介质”，又叫做“绝缘体”。组成电介质的原子或分子中的正负电荷束缚得很紧，在一般条件下不能相互分离，因此在电介质内部能作自由运动的电荷（电子）极少，电导率均在10－8西门子/米以下。当外电场超过某极限值时，电介质被击穿而失去介电性能。电介质在电气工程上大量用作电气绝缘材料、电容器的介质及特殊电介质器件（如压电晶体）等。在电介质中的两个点电荷之

电介质都有它自身的ε，不同物质的介电常数各不相同。

【介电常数】又称为“电容率”或“相对电容率”。在同一电容器中用某一物质作为电介质时的电容与其中为真空时电容的比值称为该物质的“介电常数”。介电常数通常随温度和介质中传播的电磁波的频率而变。电容器用的电介质要求具有较大的介电常数，以便减小电容器的体积和重量。

【电场】存在于电荷周围，能传递电荷与电荷之间相互作用的物理场叫做电场。在电荷周围总有电场存在；同时电场对场中其他电荷发生力的作用。观察者相对于电荷静止时所观察到的场称为静电场。如果电荷相对于观察者运动时，则除静电场外，同时还有磁场出现。除了电荷可以引起电场外，变化的磁场也可以引起电场，前者为静电场，后者叫做涡旋场或感应电场。变化的磁场引起电场。所以运动电荷或电流之间的作用要通过电磁场来传递。

【电场强度】电场强度是用来表示电场的强弱和方向的物理量。电场强度矢量，常用 来表示，电场中某一点的电场方向可用试探点电荷（正电荷）在该点所受电场力的方向来确定；电场强弱可由试探电荷所受的力F与试探点电荷带电量q的比值（F/q）来确定，也就是说某点电场的强弱等于单位电荷在该点所受力的大小。试探点电荷应该满足两个条件；（1）它的线度必须小到可以被看作点电荷，以便确定场中每点的性质；（2）它的电量要足够小，使得由于它的置入不引起原有电场的重新分布。电场强度的实用单位为伏特/米或牛顿/库仑。常用的单位还有伏特/厘米。由库仑定律和电场强度的定义可知，点电荷q在电场中某一点所受的电场力 ，等于该点电场强度E和电荷q的乘积，即 =q 。如果是正电荷， 和 同方向，如果是负电荷， 和 反方向。电场强度和电场力虽然有着密切的联系，但它们是两个不同的概念，电场强度完全由电场本身的性质所决定，而电场力是

荷q，但 的量值与q无关，因为电荷在电场中某一指定点所受的力 是和电荷的电量q成正比。所以对指定点来说， 与q的比值是不变量。

【电动力学】研究电磁运动一般规律的科学。它以麦克斯韦方程组和洛仑兹力公式为出发点，运用数学方法，结合有关物质结构的知识，建立完整的电磁理论，分别从宏观和微观的角度来阐明各种电磁现象。同量子理论结合又产生了量子电动力学。

【电子的发现】19世纪末，电学兴起，这提供了破坏原子的方法。在低压气体下放电，原子被分为带电的两部分。1897年，美国的汤姆逊在研究该两部分电荷时，发现其一带负电（称为电子），而另一个较重要的部分则带正电。这一事实说明原子不再是不可分割的。1895年，德国的仑琴发现X光，接着贝克勒尔及居里夫妇相继发现放射性元素。放射性元素就是可放出“某些东西”的原子。这些东西后来被称为α、β粒子，飞行很快。可穿透物质。这一穿透能力很快应用于探讨原子内部构造的工具，实验结果有时粒子毫无阻碍地通过，有时则又发生猛烈的碰撞。用汤姆逊的原子模型不能解释。1911年卢瑟福为了解释这一实验结果，提出一个新的原子模型。他证明：原子中带正电的部分必须集中于一个非常小而重的原子核里，而电子则如行星绕日般地围着原子核转动，原子核与电子间是有很大空隙的。用这一模型算出的数值，证实了实验结果。

【场的迭加原理】如果一个电场由n个点电荷共同激发时，那么电场中任一点的总场强将等于n个点电荷在该点各自产生场强的矢量和即

【电力线】电力线是描述电场分布情况的图像。它是由一系列假想的曲线构成。曲线上各点的切线方向和该点的电场方向一致，曲线的疏密程度，跟该处的电场强度成正比。电力线比较形象地表示出电场的强弱和方向。在静电场中电力线从正电荷开始而终止于负电荷，不形成闭合线也不中断。在涡旋电场中，电力线是没有起点和终点的闭合线。由于电场中的某一点只有一个电场方向，所以任何两条电力线不能相交。电力线上各点的电势（电位）沿电力线方向不断减小。

【法拉第】（Faraday，Michel，1791～1867）法拉第是著名的英国物理学家和化学家。他发现了电磁感应现象，这在物理学上起了重要的作用。1834年他研究电流通过溶液时产生的化学变化，提出了法拉第电解定律。这一定律为发展电结构理论开辟了道路，也是应用电化学的基础。1845年9月13日法拉第发现，一束平面偏振光通过磁场时发生旋转，这种现象被称为“法拉第效应”。光既然与磁场发生相互作用，法拉第便认为光具有电磁性质。1852年他引进磁力线概念。他主张电磁作用依靠充满空间的力线传递，为麦克斯韦电磁理论开辟了道路，也是提出光的电磁波理论的先驱，他的很多成就都是很重要的、带根本性的理论。他制造了世界上第一台发电机。所有现代发电机都是根据法拉第的原理制作的。法拉第还发现电介质的作用，创立了介电常数的概念。后来电容的单位“法拉”就是用他的名字命名的。法拉第从小就热爱科学，立志献身于科学事业，终于成为了一个伟大的物理学家。

【麦克斯韦】Maxwell James Clerk英国物理学家（1831～1879）。阿伯丁的马里查尔学院和伦敦皇家学院、剑桥大学教授，并且是著名的卡文迪什实验室的奠基人。皇家学会会员。在汤姆逊的影响下进行电磁学的研究，提出了著名的麦克斯韦方程式，这是电磁学中场的最基本的理论。麦克斯韦从理论上计算出电磁波传播速度等于光速，他认为：光就是电磁波的一种形态。对于统计力学、气体分子运动论的建立也作出了贡献。引进了气体分子的速度分布律以及分子之间相互碰撞的平均自由程的概念。著有《论法拉第力线》、《论物理力线》、《电磁场运动论》、《论电和磁》、《气体运动论的证明》、《气体运动论》。还著有《热理论》、《物质与运动》等教科书。

【超距作用】一些早期的经典物理学者认为对于不相接触的物体间发生相互作用，如两电荷之间的作用力以及物体之间的万有引力都是所谓的“超距作用力”。这种力与存在于两物体间的物质无关，而是以无限大速度在两物体间直接传递的。但是，电磁场的传播速度等于光速的这一事实说明电的作用力和电场的传播速度是有限的。因此“超距作用”论便自然被否定了。实际上，电磁场就是物质的一种形态，因此不需借助其他物质传递。

【导体】在外电场作用下能很好地传导电流的物体叫做导体。导体之所以能导电，是由于它具有大量的可以自由移动的带电粒子（自由电子、离子等）。电导率在102（欧姆·厘米）-1以上的固体（如金属），以及电解液等都是导体。金属和电解液分别依靠自由电子和正负离子起导电作用。

【自由电荷】存在于物质内部，在外电场作用下能够自由运动的正负电荷。金属导体中的自由电荷是带负电的电子，因为金属原子中的外层电子与原子核的联系很弱，在其余原子的作用下会脱离原来的原子而在整块金属中自由运动，在没有外电场时这种运动是杂乱无章的，因此不会形成电流。在外电场作用下，电子能按一定方向流动而形成电流。电解液或气体中的离子也都是自由电荷。

【束缚电荷】电介质中的分子在电结构方面的特征是原子核对电子有很大的束缚力，即使在外电场的作用下，这些电荷也只能在微观范围有所偏离。但它们一般不会彼此相互脱离。例如，电介质在外电场作用下从微观上看是分子发生电极化，微观电极化的宏观效果就是沿电场方向，在电介质的两端出现两种等量而异号的感应电荷。研究电介质的电性质时，应主要考虑束缚电荷的作用。

【电量】物体所带电荷的多少叫做电量。在国际单位制中，电量的单位是库仑。静电系单位制的电量为静库。物体所带电荷的量值是不连续的。单个电子的电量是电量的最小单元，其值为1.6×10－19库仑，一切带电体所带电量的数值都必须是电子电量e的整数倍。

【电离】原子是由带正电的原子核及其周围的带负电的电子所组成。由于原子核的正电荷数与电子的负电荷数相等，所以原子是中性的。原子最外层的电子称为价电子。所谓电离，就是原子受到外界的作用，如被加速的电子或离子与原子碰撞时使原子中的外层电子特别是价电子摆脱原子核的束缚而脱离，原子成为带一个（或几个）正电荷的离子，这就是正离子。如果在碰撞中原子得到了电子，则就成为负离子。

【静电平衡】在静电感应过程中，随着导体两端的正负电荷的不断积累，所产生的附加电场不断增强，直至跟导体内的外电场完全抵消。这时导体中的总电场处处为零，自由电荷不受电场力的作用，不再移动，导体两端的电荷不再增加。此时导体达到静电平衡状态。静电平衡状态的导体有如下的性质：（1）导体内部场强处处为零。（2）导体是个等势体，导体表面是个等势面。（3）导体表面上任何一点的场强都垂直于该点的表面。（4）电荷只能分布在导体的表面上。导体内部不存在净电荷。

【静电屏蔽】为了避免外界电场对仪器设备的影响，或者为了避免电器设备的电场对外界的影响，用一个空腔导体把外电场遮住，使其内部不受影响，也不使电器设备对外界产生影响，这就叫做静电屏蔽。空腔导体不接地的屏蔽为外屏蔽，空腔导体接地的屏蔽为全屏蔽。空腔导体在外电场中处于静电平衡，其内部的场强总等于零。因此外电场不可能对其内部空间发生任何影响。若空腔导体内有带电体，在静电平衡时，它的内表面将产生等量异号的感生电荷。如果外壳不接地则外表面会产生与内部带电体等量而同号的感生电荷，此时感应电荷的电场将对外界产生影响，这时空腔导体只能对外电场屏蔽，却不能屏蔽内部带电体对外界的影响，所以叫外屏蔽。如果外壳接地，即使内部有带电体存在，这时内表面感应的电荷与带电体所带的电荷的代数和为零，而外表面产生的感应电荷通过接地线流入大地。外界对壳内无法影响，内部带电体对外界的影响也随之而消除，所以这种屏蔽叫做全屏蔽。为了防止外界信号的干扰，静电屏蔽被广泛地应用科学技术工作中。例如电子仪器设备外面的金属罩，通讯电缆外面包的铅皮等等，都是用来防止外界电场干扰的屏蔽措施。

【电势能】与重力场一样，静电场是一个有势场。在静电场中所以能引入电势能的概念，是因为静电场具有势场的性质。所谓的势场，就是当点电荷q在任意静电场中运动时，电场力所做的功只取决于运动的始末位置而与路径无关。这种性质叫做有位性（有势性），具有这种性质的场叫做位场（势场）。在静电场中任意选取一个参考点，将正电荷q从该点移到静电场中的另一点P在此过程中，如果是外力反抗电场力作功，则所作的功等于q从参考点移到P点所增加的电势能。若从参考点到P点是电场力作正功则所作的功等于q所减少的电势能。假如电荷q在参考点的电势能为零，则将正电荷q由参考点反抗电场力使之移到P点所作的功就等于q在P点时所具有的电势能。通常把无穷远处定义为电势能的零点。实用上常把地球表面作为电势能的零点。在静电场中将电荷q放在由点电荷Q所激发的场中，如图3－1所示，设点电荷q从场中的P1点沿某一路径移到另一点P2，任取一元位移 ，设q在位移前后与Q的距离分别为r和r′。场力 在这一元位移上所作的元功dA=Fdlcosa。其中a是 与 的夹角，由图可

当电荷q在点电荷Q的场中运动时电场力所作的功只取决于运动电荷的始末位置，而与路径无关。任何电荷在静电场中的电势能的数值是由该电荷和电源电荷以及它们之间的相对位置所决定。电荷在匀强电场中移动时，场力所作的功可以从功的定义直接计算，即W=FScosθ=qFScosθ。也可以根据电势能的变化来计算，即W=ε始—ε终，对不均匀场，一般采用电势能的变化来计算比较方便。由于电势能等于电量q和电势Ｕ的乘积，所以电场力所作的功也可以写成为

W=qＵ始-qＵ终=q（Ｕ始-Ｕ终）。

 

【电势】电势是描写电场的一个物理量，也称为“电位”。静电场中某点的电势等于单位正电荷在该点时所具有的势能。理论上常把“无穷远”处作为电势零点，实用上则常取地球表面为电势零点。故某点的电势在数值上也等于单位正电荷从该点移到无穷远（或地面）时电场对它所作的功。这功与所经路径无关，所以场中各点的电势各有一定数值。

例如由正电荷所激发的场中的单位正电荷，从场中的某点移到无穷远时，电场力作正功，则该点的电势为正。如果是负电荷所激发的场，场中某点的单位正电荷移到无穷远处，电场力所作的功为负，则该点的电势也为负。和电势能一样，电势的概念也是因为静电场具有“功和路程无关”的性质而引入的，但电势能和试探电荷的正负大小有关，而电势完全取决于电场本身，它的数值只和场源电荷的电性、电量大小及所考虑的点的位置有关，和试探电荷的数值及存在与否无关。因为对电场中指定点

电势的单位就是由此公式规定的。正点电荷q0的电场中各点电势都是正

物理量，但电势和电场作功相联系，场强和电场力相联系，所以前者是标量，后者是矢量。在计算场的迭加问题时，电势取标量和，场强用矢量和。在匀强电场中，电荷q沿电场方向移动距离d，电场力所作的功W=qEd，而电势能改变量为qＵab，a、b为电荷q的始点和终点。根据功能关系，二者应该相等，即qEd=qＵab，

位距离的电势差（电压），方向指向电势降落的方向。对于非均匀场，

向电势降落的方向。这一关系非常重要，因为在实践中一般能直接测量的是各个导体的电势，求得电势后就可利用求导数而计算场强。直接求解含有电场强度的矢量方程是比较困难的，而求解含有电势的标量方程，相对说来较为方便（理论物理中的泊松方程和拉普拉斯方程就是电势解场的实例）。

【等势面】亦称为“等位面”。在有势场中，势的数值相等的各点所联成的面。一般规定每隔一定数值的势画一等势面，场较强的地方等势面较密，较弱的地方较疏，因此等势面是描述场分布情况的一种直观图象。例如点电荷产生的静电场，等势面是以点电荷为中心的一组同心球面，且内密外疏。电荷沿同一等势面移动时，电场力不作功，所以等势面与电场方向永远是垂直的。静电场中的任何导体的表面都是等势面；又因其内部不存在电场，它同时也是一个等势体。静电场中的电力线处处和等势面相垂直，并指向电势降落的方向。

【电势差】静电场中或直流电路中两点间电势的差值，也称为“电位差”或“电压”。数值上等于电场力使单位正电荷从一点移动到另一点时所作的功。在交流电路中，两点间的电势差在正负极大值之间作周期性变化，所以电势差只有瞬时值的意义，常用有效值表示，一般交流

用下总是从电势高的地方走向电势低的地方。假定A点的电势为ＵA，B点的电势为ＵB，而ＵA＞ＵB，把正电荷q从A点移到B点，q的电势能减少量为qＵA-qＵB即W=q（ＵA-（ＵB）=qＵAB，ＵAB就是AB两点间的电势差（或电压）。

【电子伏特】在研究原子、原子核、基本粒子等微小粒于时，往往用电子伏特作为能量单位。1电子伏特，就是带有单个电子电量的带电粒子，在电压为1伏特的两点间，在电场力作用下粒子所增加的能量。它是带电粒子加速器中的能量单位，用起来比较方便。比如说这台加速器是1亿电子伏的能量，就是说，他能把单位电荷的粒子加速而得到1亿电子伏的能量。国际通用的符号是eV。1电子伏特=1eV=1.6×10-19库仑×1伏=1.6×10-19焦耳。

【匀强电场】在电场中，各个点的电场强度的大小和方向均相同的场叫匀强电场。在匀强电场中的等势面是垂直于电力线的一族互相平行的平面。在匀强电场中，沿场强方向的两点间的电势差等于场强和这两点间距离的乘积。即场强在数值上等于沿场强方向每单位距离上的电势

电势在电场方向上的变化是均匀的。

 

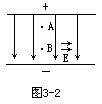
【电场强度与电势差】在匀强电场中，电场强度与电势差之间的关系为ＵAB=Ed，其中d是AB两点间沿电场方向的距离。如图3－2所示。对于非匀强电场，单位正电荷从P点移到参考点P0时电场力所作的功，叫做P点的电位（或电势），记作Ｕ。既然场力所做的功与场强有关。就应找到电势与场强的关系。点电荷q从P到P0点时场力所做的功

位移向量的标量积）。对场中任意两点电势之差（电压）与电场强度之 位是点函数，电压不是点函数。应该养成“对一点谈电势，对两点谈电压”的习惯；（2）在许多情况下不但要关心两点电压的绝对值，而且要关心这两点的电势谁高谁低。一般以ＵAB表示ＵA-ＵB，（称为“A对B的电压”），于是从ＵAB的正负便表示了A、B电位的高低；（3）静电场力所作的功与路径无关，所以当电场确定时，两点的电压就完全确定，但电位却与参考点的位置有关。因此说到某点的电势时，一定要明确指出参考点。只要在同一问题中选定一个参考点，电势就有确定的

表示的为电势与场强的微分关系。此式说明，（1）一点的场强与过该点的等位面垂直，而且指向电位减小的方向；（2）某点场强的大小等于该点电势沿等势面法向的变化率（沿法向的方向导数）。

【电场中的带电粒子】在静电场中的带电粒子总是沿着电场方向或逆着电场方向受到电场力的作用。带正电荷的粒子所受的力是沿电场方向的，带负电荷的粒子所受的力则沿着电场的反方向。也就是说，带正电荷的粒子从电势高的地方向电势低的地方做加速运动。而带负电荷的粒子则从电势低的地方向电势高的地方做加速移动。例如带正电粒子从高电位开始运动到低电位。如果高电位与低电位之间的电势差为Ｕ，则在这段运动期间，电场力作功为W，则W=qＵ。到达低电势时质量为m

电粒子所带的电量，以及运动始末的电势差值有关。对同样的电势差，

场或非匀强场均适用，因为电场力所作的功总是qＵ。如果我们在垂直于带电粒子前进的方向上加一个匀强电场，则运动的带电粒子将要发生偏转。

【加速器】加速器是用人工方法把带电粒子加速到较高能量的装置。利用这种装置可以产生各种能量的电子、质子、氘核、α粒子以及其它一些重离子。利用这些直接被加速的带电粒子与物质相作用，还可以产生多种带电的和不带电的次级粒子，象γ粒子、中子及多种介子、超子、反粒子等。目前世界上的加速器大多是能量在100兆电子伏以下的低能加速器，其中除一小部分用于原子核和核工程研究方面外，大部分用于其他方面，象化学、放射生物学、放射医学、固体物理等的基础研究以及工业照相、疾病的诊断和治疗、高纯物质的活化分析、某些工业产品的辐射处理、农产品及其他食品的辐射处理、模拟宇宙辐射和模拟核爆炸等。近年来还利用加速器原理，制成各种类型的离子注入机。以供半导体工业的杂质掺杂而取代热扩散的老工艺。使半导体器件的成品率和各项性能指标大大提高。很多老工艺不能实现的新型器件不断问世，集成电路的集成度因此而大幅度提高。

【密立根】Millikan，Robert Andrews（1868～1953年）美国物理学家。1910～1917年，应用带电油滴在电场和重力场中运动的方法，精确测定单个电子的荷电量，从而确定了电荷的不连续性这就是著名的密立根油滴实验。1916年曾验证爱因斯坦的光电效应公式，并测定普朗克常数。在宇宙射线方面也做了一些工作。

【基本电荷】原子中的电子和原子核中的质子带有等量异种电荷。它们所带的电量都是e=1.602×10－19库仑，这一电量是不可分割的最小电量，称之为基本电荷，也是电量的基本单位，这是密立根通过他的油滴实验验证的结果。不同离子本身可以带有e，2e，3e，……的电量。

【电容器】电路中用以积储电能的基本元件。实际上用得最多的是由两个导体组成的电容器，常见的电容器有平行板电容器以及圆柱电容器两种。在两个导体间由电介质相隔。所用的电介质有固体的、气体的（包括真空）和液体的。按型式分，电容器有固定的、可变的和半可变的三类。按极片间使用的介质分，则有空气电容器、真空电容器、纸介电容器、塑料薄膜电容器、云母电容器、陶瓷电容器、电解电容器等。电容器在电力系统中是提高功率因数的重要器件；在电子电路中是获得振荡、滤波、相移、旁路、耦合等作用的主要元件。电容器电量与电压的比值只与电容器本身有关。

【电容】表征导体由于带电而引起本身电势改变的物理量。一个导体的电势，非但与其本身的电荷有关，且与周围的介质和其他导体的电荷有关。当其他导体的电势都维持一定（例如接地）时，一个导体的电势正比于其本身的电量，这个导体的电容就以其电量与电势的比值来量度；电容器的电容以一个极板的电量与两极板间电势差的比值来量度。电容的大小取决于极板的形状、大小、相对位置以及极板间电介质的介

压升高，就要给它提供电量（充电），使电压升高一个单位所需的电量，在数值上等于它的电容。要注意，电容器和电容是两个不同的概念。前者是两个导体的组合。后者是描写该组合性质的物理量。对平行板电容

平行板之间的距离， L为圆柱电容器的长度，R1和R2是圆柱和球的内外径。在电容器的两个导体之间充入电介质可以使电容增大。实用中常利用这个方法增大电容器的电容。充入均匀介质后，上述的三种形式的电容都要乘以一个大于1的常数ε（由电介质的性质决定），即电容增至ε倍。

【电容器的串联】多个电容器串联时，流入电容器组的电量q全部进入第一个电容器的左边板（设A端接电池正极），其右边板因感应而带-q，于是第二个电容器在板带+q，右板带-q。见图3－3所示，故

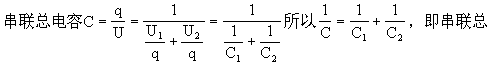
电容的倒数等于每个电容的倒数之和。

 

 

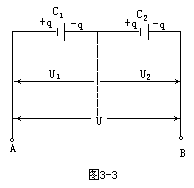
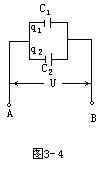
【电容器的并联】如图3－4所示为两个电容器并联，其中Ｕ表示两端A与B之间的电压（绝对值），q表示充电时流入电容器的总电量。

=C1+C2即并联总电容等于每个电容器电容之和。电容器并联时电容增大，串联时电容减小。实用中可根据需要而选用并联和串联。

【电容器的击穿】串联时总电压分配于各电容器上，这时电容器的电容减小，却提高了耐压能力。耐压能力是指电容器忍受外加电压的能力。每个电容器的电压都有一个界限，超过此界限时，会产生过大的内部场强，从而使所充的绝缘材料（电介质）变为导体以致于损坏电容器，这种现象叫“电容的击穿”。

【电流】带电粒子的运动叫做“电流”。例如金属中自由电子在电场作用下的定向运动，液体或气体中正负离子相互沿相反方向流动。在电流发生的同时，还会伴生出其他效应：电流的周围存在着磁场；电流通过电路时使电路发热；通过电解质时引起电解；通过稀薄气体时，在适当条件下导致发光等等。由于电流形成过程的不同，除传导电流外，还有对流电流和位移电流。所谓的对流电流是带电介质或介质中的带电部分不是由于电场作用而在空间运动时形成的电流。同一般电流一样，对流电流的周围也存在着磁场。例如当带电的平行板电容器绕垂直于板面的轴急速旋转时就出现磁场。由于带电体在原来没有电磁场的空间中匀速运动不须外力维持（如果不计空气阻力），所以对流电流不需要电势差来维持，它不引起热效应。致于位移电流被定义为电位移矢量随时间的变化率。麦克斯韦首先提出这种变化将产生磁场的假设，故称“位移电流”。实际上位移电流只表示电场的变化率，与传导电流不同，它不产生热效应、化学效应。继电磁感应现象发现之后，麦克斯韦的这一假设更深入一步揭露了电现象和磁现象之间的紧密联系。位移电流是建立麦克斯韦方程组的重要依据。在中学课本中主要讨论的是传导电流。在导体中存在持续电流的条件是保持导体两端的电势差（电压）。

【电流强度】单位时间内通过导体某一横截面的电量为该截面处的电流强度。即通过导体某一横截面的电量q，跟通过这些电量所用的时

强度的单位是安培或简称安，通常用“A”表示。常用的单位还有毫安（即10-3A表示为mA）、微安（即10-6A表示为μA）。金属导体中的电流是自由电子在外电场作用下漂移运动的结果。真空中的电子流，是由灼热的金属或金属氧化物表面发射出来的电子，在真空中由外加电场加速作定向运动而形成电流。如阴极射线就是真空中的高速电子流。气体中的电流，是在稀薄气体中，两端电极上加有足够高的电压时，从阴极表面逸出电子必向阳极运动，在电子向阳极运动的过程中，由外加电压作用可获得较大的动能，这些电子与中性气体分子相碰，使其电离（碰撞电离），同时正离子还能向阴极运动，再次从阴极表面击出电子（二次电子发射）。所以碰撞电离和二次电子发射都使气体中出现离子和大量电子，它们在外电场作用下定向移动，形成气体中电流。当对电解质溶液的两极加上电压时，将使溶液中作热运动的正负离子迭加一个漂移运动而形成电流。注意，由于在溶液中有正负两种电荷沿相反方向运动，所以总电流应该是正离子电流和负离子电流的绝对值的和。

【稳恒电流】在恒定电阻的电路中，加上电压恒定的电源，便产生大小和方向都不随时间改变的电流，称为“稳恒电流。”

【电流密度】描述电路中某点电流强弱和流动方向的物理量。其大小等于单位时间内通过垂直于电流方向单位面积的电量，以正电荷流动的方向为正方向。注意电流密度和电流强度都是描写电流的物理量。然而电流强度是一个标量，是描写导体中通过一个截面的电流量（不是点函数）；电流密度是一个矢量点函数，是描写导体中某一点的电流方向和通过该点垂直截面的电流强度。

【欧姆定律】欧姆定律是研究在稳恒电流通过的电路中，电流、电压和电阻间的相互关系。这个关系可表示为两种形式：部分电路欧姆定律和全电路（闭合电路）的欧姆定律。当一段导体两端存在电压时，导体内部就出现电场，载流子就要在电场力的作用下发生定向运动，形成电流。关于电流与电压之间的定量关系，德国科学家欧姆通过大量的实

R的数值取决于导体的材料，形状、长短、粗细及温度等。当这些因素不变时R为常数，只有当R为常数时才可以说I与Ｕ成正比。导体的R值越大流过它的电流I越小，可见R值反映导体对电流的阻碍程度，称为导体的电阻。在学习欧姆定律时应注意的是：（1）欧姆定律对金属导体及通常情况下的电解液都很好地成立，但对半导体二极管、真空二极管以及许多气体导电管等元件都不适用。（2）当导体内部含有电源时，

路的欧姆定律。

【电动势】电源内部非静电力移送单位正电荷，将其从电源的负极移至正极所作的功，叫做电源的电动势。电动势的单位是伏特。电源提供电能必须通过非静电力对电荷做功的方式从其他形式能量转变而来。例如，在具有一定负载的直流电路中，若要维持电路中的电流恒定不变，就必须设法维持电路两端有恒定的电势差（电压）。这就必须有非静电力不断对电荷作功来实现。在外电路电流是由高电势的正极流向低电势的负极。则在电源内部必须由非静电力将负电荷移到负极上，并将正电荷送到正极上。才能达到维持电路两端的恒定电势差。

【电阻定律】对于由一定材料制成的横截面积均匀的导体，在一定的温度下，它的电阻R和导体的长度l成正比，和横截面积S成反比。

导体横截面积不均匀，或者电阻率ρ不均匀时，可将其沿长度l的垂直

【电阻率】表征物质导电性能的物理量。也称“体积电阻率”。电阻率越小导电本领越强。用某种材料制成的长1厘米、横截面积为1平方厘米的导体电阻，在数值上等于这种材料的电阻率。也有取长1米、截面积1平方毫米的导电体在一定温度下的电阻定义电阻率的。此两种定义法定义的电阻率在数值上相差4个数量级。如第一种定义，铜在20℃时的电阻率为1.7×10-6欧姆·厘米。而第二种定义电阻率为0.017欧姆·毫米2/米。电阻率的倒数称为电导率。电阻率ρ不仅和导体的材料有关，还和导体的温度有关。在温度变化不大的范围内，几乎所有金属的电阻率随温度作线性变化，即ρ=ρ0（1+αt）。式中t是摄氏温度，ρ0是0℃时的电阻率，α是电阻率温度系数。由于电阻率随温度的改变而改变，所以对某些电器的电阻，必须说明它们所处的物理状态。如220伏、100瓦电灯的灯丝电阻，通电时是484欧姆，未通电时是40欧姆。另外要注意的是：电阻率和电阻是两个不同的概念。电阻率是反映物质对电流阻碍作用的属性，电阻是反映物体对电

制中电导率的单位是西门子/米。

【超导体】在温度和磁场都小于一定数值的条件下，许多导电材料的电阻和体内磁感应强度都突然变为零的性质。具有超导性的物体叫做“超导体”。1911年荷兰物理学家卡曼林-昂尼斯（1853～1926年）首先发现汞在4.173K以下失去电阻的现象，并初次称之为“超导性”。现已知道，许多金属（如铟、锡、铝、铅、钽、铌等）、合金（如铌—锆、铌—钛等）和化合物（如Nb3 Sn、Nb3Al等）都是可具有超导性的材料。物体从正常态过渡到超导态是一种相变，发生相变时的温度称为此超导体的“转变温度”（或“临界温度”）。现有的材料仅在很低的温度环境下才具有超导性，其中以Nb3Ge薄膜的转变温度最高（23.2K）。1933年迈斯纳和奥森费耳德又共同发现金属处在超导态时其体内磁感应强度为零，即能把原来在其体内的磁场排挤出去；这个现象称之为迈斯纳效应。当磁场达到一定强度时，超导性就将破坏，这个磁场限值称为“临界磁场”。目前所发现的超导体有两类。第一类只有一个临界磁场（约几百高斯）；第二类超导体有下临界磁场Hc1和上临界磁场Hc2。当外磁场达到Hc1时，第二类超导体内出现正常态和超导态相互混合的状态，只有当磁场增大到Hc2时，其体内的混合状态消失而转化为正常导体。现在已制备上临界磁场很高的超导材料（如Nb3Sn的Hc2 达22特斯拉，Nb3Al0.75Ge0.25的Hc2达30特斯拉），用以制造产生强磁场的超导磁体。超导体的应用目前正逐步发展为先进技术，用在加速器、发电机、电缆、贮能器和交通运输设备直到计算机方面。1962年发现了超导隧道效应即约瑟夫逊效应，并已用于制造高精度的磁强计、电压标准、微波探测器等。近两年来，中国、美国、日本在提高超导材料的转变温度上都取得了很大的进展。1987年研制出YBaCuO体材料转变温度达到90～100K，零电阻温度达78K，也就是说过去必须在昂贵的液氦温度下才能获得超导性，而现在已能在廉价的液氮温度下获得。1988年又研制也CaSrBiCuO体和CaS- rTlCuO体，使转变温度提高到114～115K。近两三年来，超导方面的工作正在突飞猛进。

【欧姆】Ohm，Georg Simon（1787～1854年）德国物理学家。1787年生于欧蓝格，毕业于欧蓝格大学。1826年发现导体的电阻、电流与电动势之间的关系定律现称欧姆定律。此定律先未受重视，直到1833年欧姆在纽仑堡任物理学教授时才渐为人所知。1849年欧姆任慕尼黑大学物理学教授。后人为纪念其对电学贡献，以其名做为电阻的单位。

【电功】电流通过电路时，电场力对电荷作的功叫做电功。在国际单位制中，电功的单位是焦耳。有时用千瓦·小时（即通常所说的“度”）。

式子，只有当电路是纯电阻电路，并没有反电动势存在时才成立。如果电路负载中存在反电动势，要分清三种形式公式的适用范围以及它们的物理意义。当电路负载中有反电动势时，则W=IＵt为整个负载的总功，而W=I2Rt则仅表示负载所消耗热的那部分功。

【电功率】每单位时间内电场力所作的功叫做电功率。在国际单位制中，电功率的单位是瓦特（常用的单位还有马力、千克力·米/秒）。

电阻，没有反电动势存在时上列各式都成立。如果电路负载中存在反电动势，则要分清此三公式的适用范围及其物理意义。若电路负载中存在反电动势，则P=IＵ为整个负载的总功率，而P=I2R则仅表示负载所消耗热的那部分功率。例如，当电路中接有直流电机时，如果加在电机两端电压为Ｕ，正常工作时通过电流为I。则当电枢线圈转动时作切割磁力线运动而产生感生电动势，这一感生电动势和外加电压方向相反，因

（输入功率），I正ε反为克眼反电动势所消耗的功率，即转变为机械能

，只有在纯电阻电路中，三个公式可以通用，而在有反电动势的电路中（含源电路）三者不能混淆。

【焦耳定律】导体在通过电流时会有热量发出。英国物理学家焦耳通过实验总结出如下的规律：电流通过导体时放出的热量Q与电流I的平方、导体的电阻R以及通电时间t成正比，即Q=KI2Rt，这就是焦耳定律。电流通过导体时按这一规律所放出的热量叫做焦耳热。若分别以焦耳、安培、欧姆及秒等为国际制单位测量热量、电流、电阻及时间，实验测得K=1焦耳/欧姆·安培2·秒。故上式变为

当n个导体串联时，由于通过所有导体的电流都相等，用前式来比较个别导体所放出的热量较为方便。当n个导体并联时，在各个导体上的电流各不相同，但它们两端的电压都相等，在这种情况下用后式较为方便。必须再次强调说明的是，当电路上有电流通过时，不但产生热的效应，而且还可以产生其他不同的效应。例如，在一般的电路中，除有纯电阻外还有电动机，电解槽等用电器，那么电能除部分转化为热（内能）外，还要转化为机械能、化学能等。因此，只有当电路为纯电阻，而且整个电路不能运行时，电流所做的功才全部变为热，否则W=ＵIt总要大于电流的纯电阻上产生的热量Q=I2Rt。

 

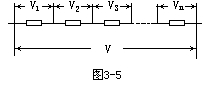
【串联电路】多个电阻按图3－5所示方式的联接叫做串联。串联电路的基本特征是只有一条支路，由此出发可以推出串联电路有如下五个特点：（1）流过每个电阻的电流相等。因为直流电路中同一支路的各个截面有相同的电流强度。（2）总电压（串联电路两端的电压）等于分电压（每个电阻两端的电压）之和，即Ｕ=Ｕ1＋Ｕ2＋…+Ｕn。这可由电压的定义直接得出。（3）总电阻等于分电阻之和。把欧姆定律分别用于每个电阻可得Ｕ1=IR1，Ｕ2=IR2，…Ｕn=IRn代入Ｕ=Ｕ1+Ｕ2＋…＋Ｕn并注意到每个电阻上的电流相等，得Ｕ=I（R1＋R2＋…＋Rn）。此式说明，若用一个阻值为R=R1＋R2+…+Rn的电阻元件代替原来n个电阻的串联电路，这个元件的电流将与原串联电路的电流相同。因此电阻R叫原串联电阻的等效电阻（或总电阻）。故总电阻等于分电阻之和。（4）各电阻分得的电压与其阻值成正比，因为Ｕi=IRi。（5）各电阻分得的功率与其阻值成正比，因为Pi=I2Ri。

 

 

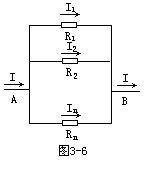
【并联电路】多个电阻按图3－6所示方式的联接叫并联。由n个电阻并联而成的那部分电路有两个节点，n条支路。并联电路有如下五个主要特点：（1）每个电阻两端电压相等。因为每个电阻两端都是A点和B点。（2）总电流等于各分电流之和，即I=I1+I2+…+In。因为从节点A流入的电流一定等于从节点B流出的电流。（3）总电阻的倒数

满足上式的R叫做并联电路的等效电阻（或总电阻），可见总电阻的倒数等于分电阻的倒数和。对两个电阻并联的简单情况，总电阻可以写成

多个电阻则可依此类推。图3－7所示是一个电阻R等效代替两个并联电阻的情况。（4）各电阻分得的电流与其阻值成反比。这一点可由Ii=

上的几个特点，不难得出结论：（1）并联电阻必小于每个参与并联的电阻的阻值。（2）当两个并联电阻的阻值R1和R2悬殊时（R1<<R2），并联总电阻R近似等于小电阻的阻值（R≈R1）。特别是，如果用一条导线（R1≈0）与一个电阻R2并联，总电阻就近似为零。这种情况称为“R2被短路”或“R2被短接”。（3）当两个电阻相等时，并联总电阻等于其中一个电阻的一半。图3－8所示是一个混联电路。计算总电阻时，关键是正确判断两个电阻是串联、并联，还是既非串联又非并联。每个电阻都有两个端点。如果两个电阻各有一端相联，而且联接点上不再引出导线接其他元件，这两个电阻就是串联。串联时两电阻通过的电流必相等。如果一个电阻的两端分别与另一电阻的两端相联，而且联接点上还引出导线联接其他元件，这两个电阻就是并联。并联时两电阻上的电压必相等。例如图3－8中的R1与R4的联接方式既不保证它们的电流相等又不保证它们的电压相等，所以它们既非串联又非并联。而R3和R5的接法却满足并联定义，故可把它们的并联总电阻求出（30欧姆），以一个30欧姆的电阻代替R3和R5画成图b，依次一步步简化，最后便可求得RAB=30欧姆。

 

【电流表】用以测量电流的仪表叫做电流表。常用的电流表是磁电式电流表（亦称磁电式表头）。它的主要组成部分是一块永久磁钢及一个可动线圈。当被测电流流过线圈时，它将受磁场的力矩而偏转。电流的大小由偏转的角度来反映，可由固定在线圈上的指针在刻度盘上的位置读出。因为偏转角度与电流成正比，所以刻度盘上的刻度是均匀的。由于测量的需要不同，电流表分为安培表，毫安表和微安表。当被测电流超过电流表的量程时，指针的偏转将超出刻度的界限，不但不能读出电流的数值，还会把指针碰弯，电流太大时甚至会因过量的焦耳热而把线圈烧断。所以，每个表头所能测量的范围都有一限度，这就是表头的量程（或称满刻度电流）。

 

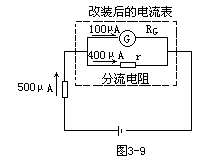
【电流表的分流】电流表本身线圈能够承受的电流不超过毫安级。为了扩大其量程，可以对表头进行改装，使之能够测量几安培，甚至更大的电流。设表头的量程为100微安，欲要测500微安的电流，可以在表头上并联一个电阻r如图3－9所示。适当选择r值，可使被测电流的1/5（即100微安）流过表头，这样指针就恰好指在刻度的最右端。当被测电流为500微安以下的任一数值I时，由并联电路的计算可知，流过表头的电流IG恒与I成正比，因此只需把刻度盘的读数乘以5便得被测电流的数值。因为电阻r起到分流作用，所以叫做分流电阻。表头与分流电阻的总体组成一个量程扩大了的新电流表（亦称毫安表，安培表等，视扩大后的量程而定）。一般地说，如果要把量程扩大n倍（在

圈的电阻（也称表头的内阻）。

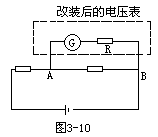
【电压表】用以测量电压的仪表叫做电压表。电压表所能测量的最大电压叫做电压表的量程。表头本身可台看作一个电压表，因为表头两端加上被测电压时，线圈就有电流通过，指针就有偏角。由于线圈的电阻一定，其电流与电压成正比，因此指针的偏角可以反映被测电压的数值。只要把刻度盘接电压标定，就可以把表头当作电压表使用。然而这种电压表的量程很小。例如，一个电流量程为100微安、电阻为2000欧姆的表头，最多只能测量100微安×2000欧姆=0.2伏特的电压。在实际测量中，被测电压往往大大超过表头允许的电压。要测量这种电压就需对表头进行改装。每个表头之所以都有一个电压量程，关键在于当电压超过这个量程时流过表头的电流就超过了它的电流量程。如果用适当的电阻与表头串联来减小流过表头的电流，那么串联而成的电压表就允许承受较大的电压，或者说这个表头与电阻R串联构成一个量程较大的电压表。图3－10所示是用这种改装后的电压表测量电路中A、B两点电压的电路图。对同一个表头来说，要改装成量程大的电压表，所需串联的电阻R也越大。设表头的电流量程为IGm，内阻为RG，欲改装成量程为Ｕm的电压表。因为串联电路的总电压Ｕm=IGmR

表之分。

 

 

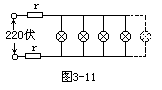
【线路上的电能损失】在日常生活中常会发现，家庭中用电，在用电高峰时，显得灯不很亮，甚至有时洗衣机等都不能正常运转。这就是因为电路里并联使用的用电器越多，在干路里的总电流越大，而干路输电的导线总要有一定大小的电阻，电流越大，在导线的电阻上降压越多，因而加在用电器上的电压就越小。故造成电灯不很亮。机器不能正常运转的情况。例如，如图3－11所示的为100盏“220伏，40瓦”的电灯并联在220伏的线路电压上。其线路电阻为2r=2欧姆（即图中的r=1欧姆）。（1）在只打开其中10盏灯时每盏灯的电压和功率；（2）100盏灯全部打开时每盏灯的电压和功率。在只打开10盏灯时，每盏灯

=1.8×2=3.6（伏特）。这时加在电灯上的电压为（220-3.6）伏=216

2×16×1=32伏，这时电灯上的电压只有（220-32）伏=188伏。每盏

=39瓦。从这个例子中可知，用电量也是要有限度的，不能像有人认为的那样，只要有电就可随便用。从此例中也应更明确节约用电的道理和重要性。

【闭合电路的欧姆定律】通过闭合电路的电流I跟电源的电动势ε成正比，跟电路电阻与电源的内阻和R＋r（即闭合电路的总电阻）

过。通常称电源以外的电路叫外电路，电源以内的电路叫内电路。当电流流过电阻时，电能将转化为热能，而当电流流过电源时，电源中的非静电力作用将其他形式能转化为电能。从能量守恒定律可以写出ε

电压、内电压、电动势三者既有区别，又有联系。当外电阻 R→∞时，即外电路开路，电流为零，内电压为零，则路端电压等于电动势。当R

零，则内电压等于电动势。从微观上看。金属中存在着大量的自由电子，自由电子和振动着晶格原子发生碰撞，碰撞非常频繁，一般情况下，每秒可达1014次。在无外电场作用下，自由电子在任一方向上的运动几率均相等，因此这些自由电子的运动可看作热运动，其速度矢量以及其平均值都等于零。如果加上外电场，那么在相邻两次碰撞之间的一段时间内，电场对自由电子起加速作用，这时形成的速度除热运动外还有沿电

间。所以金属导体中存在电场时，自由电子的平均速度就等于由电场所

自由电子最后一次碰撞到观察的这一时刻间的平均时间。因为

一般不同，这表明不同金属在同一场强作用下出现不同的电流密度，即不同金属的导电性能不同。实际上这个比值就是金属的导电率σ。对闭

式。即ε=Ｕ+Ir。

【路端电压】简称“端电压”。电路接通时，电源两极间的电压。它等于电源的电动势减去内电路的电压，即Ｕ=ε－Ir。一般来说，电源的电动势和内阻都是定值。所以外电路的端电压是随着电流的大小而变的。电流大Ｕ就减小，由此可见端电压是随着负载的变化而变化的。当没有电流，即外电路切断时，Ir=0，这时端电压就等于电源的电动热，当外电路负载电阻R=0时，路端电压为零，这时电流强度为ε/r。这种现象叫做“短路”。在使用电器时要严防这种现象发生。

【基尔霍夫定律】确定电路中有关量的两个定律。第一定律：在任一时刻流入电路中某一分节点的电流强度的总和，等于从该点流出的电流强度的总和。第二定律：在电路中任取一闭合回路，并规定正的绕行方向，其中电动势的代数和，等于各部分电阻（在交流电路中为阻抗）与电流强度乘积的代数和。这两个定律是德国物理学家基尔霍夫首先提出的。两个定律的数学式分别为ΣI=0，ΣE-ΣIR=0。在应用节点电流方程时，通常规定流进节点的电流为正，流出节点的电流为负。节点电流方程不仅对节点适用，还可把它推广到任意假定的封闭面。可以把几个元件放入一个假想的封闭面中，也可把一部分电路划入。这时流进封闭面的电流和流出的电流相等。在应用回路电压方程时，必须先选定沿回路绕行的方向，以便定出电阻上电压降或电源的电动势的正负。当绕行方向和流过电阻的电流方向一致时，电流应取正值，即减去正IR，反之，取负值；当绕行方向从电源负极到正极时，电动势应取正值，反之取负值。

【电池】是将化学能直接转变为电能的装置。主要部分包括正负两个电极和电解质。使用时，用导线把两个电极和外电路联接，即有电流流过，称为放电，从而获得电能。放电到一定程度后，经过直流电源给其充电，能复原续用的称蓄电池，如汽车中常用的铅蓄电池；不能复原蓄用的称“原电池”，如手电筒中常用的锌干电池。除了化学电池外，还有从其他形式的能转为电能的电池，如温差电池、太阳能电池（光电池）、原子电池等。

【电池组】把两个或多个电池连接起来作为电源使用的一种组合。如果将电池串联使用，则串联电池组的电动势等于各个电池电动势之和，串联电池组的内电阻等于各个电池内电阻之和。对n个电动势一样的电池串联而成的电池组，有ε串=nε，r串=nr。对相同电动势的n个电池

给较高的电压。而并联电池组不能给出高电压，但可以供给较强的电流。有时为了两者兼而有之，把电池按不同的需要组成一定形式的串并联混用的电池组。

【电流表的测量误差】如果我们用电流表测量某电路中的电流。必须把电流表串在这个电路中，因为电流表有内阻（等于表头内阻与分流电阻r 的并联总电阻），它的串入必然使电路的电流变小，而电流表的读数只能反映这个变小后的电流，这就带来了误差。显然，电流表内阻Ri越小误差越小。Ri等于表头内阻Rg与分流电阻r的并联值，因r与Rg成正比，可见Rg越小Ri就越小。所以在量程相同的表头中，由内阻较小的表头改装成的电流表有较小的内阻，因而由于内阻带来的测量误差也就越小。

【电压表测量的误差】在用电压表测量电路两端的电压时，必须将电压表与被测电压段并联。并联的结果将影响被测段的电压和其它段的电压分配，因此测出的电压只能是接入电压表后的电压值，显然，电压表内阻越大误差越小。电压表的内阻等于表头内

一定时，其内阻（Rg+R）与所用表头的量程Igm成反比。因此在实用中，为了减小误差，应尽可能采用Igm较小的表头。

 

【欧姆表的测量原理】欧姆表是测量电阻的仪表。图3－12所示为欧姆表的测量原理图。虚线方框内是欧姆表的内部结构（简化），它包含表头G、直流电源ε（常用干电池）及电阻RΩ。当被测电阻RX接

的电压（测量时基本上不变）。由上式可知，对给定的欧姆表，I与RX是一一对应的关系，所以由表头指针的位置可以知道RX的大小。为了读数方便，事先在刻度盘上直接标出欧姆值。

和电压表不同，欧姆表的刻度有三方面的特点：（1）电流表及电压表的刻度越向右数值越大，欧姆表则相反，这是由于RX越小I越大造成的。每个欧姆表刻度盘的最右端都标以“0Ω”的数值，因为总可以选择RΩ的值以保证RX=0时流过到头的电流恰好等于它的满刻度电流IGm。（2）磁电式电流表及电压表是均匀的，欧姆表的刻度都不很均匀，越向左越密。这是因为刻度的疏密程度取决于电流对电阻的变化率，即取

刻度赵密。（3）电流表及电压表的刻度都是从0到某一确定的值，因此每个表都有一个确定的量程。但欧姆表的刻度却总是从0到∞欧姆。

【欧姆表中值电阻】当RX=0时表头电流等于它的满刻度电流IGm，

（RΩ+RG）是一个定值，所以每个RX值都对应一个确定的I/IGm值。I/IGm这个数值是很有实际意义的，正是它唯一地决定着表针的位置，例

表针指在刻度盘的中间，等等。即每个RX值决定一个I/IGm值，而每个I/IGm值又决定表针的一个位置。如果两个欧姆表有不同的（RΩ＋RG）值，同一RX就对应不同的I/IGm，即对应不同的表针位置，它们的实际情况就不一样。反之，只要两个欧姆表的（RΩ＋RG）值相等，它们的刻度情况就完全相同（可以共用一个刻度盘。欧姆表的（RΩ＋RG）叫做它的“中值电阻”，因为当RX=RΩ＋RG时，则I/IGm=1/2，表针恰指正中。也就是说：中值电阻唯一地决定了欧姆表的刻度。

【欧姆表的测量范围】虽然任何欧姆表的刻度都从0到∞欧姆。但因为越向左边刻度越密，所以当被测电阻Rx很大时就难以得到准确读数。这时就应换用一个中值电阻较大的欧姆表。若此表的中值电阻是原表的中值电阻的100倍，则该表刻度盘的中值位置的电阻值即为原表的100倍。人们通常用的万用表的电阻档都是有几个中值电阻，以便取不同的档次。例如，最常用的欧姆表有×1、×10、×100、×1000等档。

【欧姆表调零】干电池在使用一段时间后两端电压有所下降，于是当Rx=0时表针不能指零。为了解决这一问题采用一个可变电阻R0与表

（RΩ+RG+R0）。当电池电压改变后，调整R0可以保证当Rx=0时表针指零。但R0的改变会导致中值电阻的改变，因此使刻度情况改变。然而刻度盘的刻度却无法改变，这就带来误差（除Rx=0以外，测量任何Rx都有误差）。

 

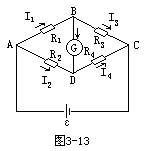
【惠斯通电桥】惠斯通电桥是一种可以精确测量电阻的仪器。图3－13所示是一个通用的惠斯通电桥。电阻R1，R2，R3，R4叫做电桥的四个臂，G为检流计，用以检查它所在的支路有无电流。当G无电流通过时，称电桥达到平衡。平衡时，四个臂的阻值满足一个简单的关系，利用这一关系就可测量电阻。平衡时，检流计所在支路电流为零，则有，（1）流过R1和R3的电流相同（记作I1），流过R2和R4的电流相同（记作I2）。（2）B，D两点电位相等，即ＵB=ＵD。因而有I1R1=I2R2；

个阻值已知，便可求得第四个电阻。测量时，选择适当的电阻作为R1和R2，用一个可变电阻作为R3，令被测电阻充当R4，调节R3使电桥平衡，

电阻而且可利用高灵敏度的检流计来测零，故用电桥测电阻比用欧姆表

分条件。电桥不平衡时，G的电流IG与R1，R2，R3，R4有关。利用这一关系也可根据IG及三个臂的电阻值求得第四个臂的阻值，因此不平衡电桥原则上也可测量电阻。在不平衡电桥中，G应从“检流计’改称为“电流计”，其作用而不是检查有无电流而是测量电流的大小。可见，不平衡电桥和平衡电桥的测量原理有原则上的区别。利用电桥还可测量一些非电学量。例如，为了测量温度变化，只需用一种“热敏元件”把它转化为电阻的变化，然后用电桥测量。不平衡电桥往往用于测量非电学量，此外还可用于自动控制和远距离联动机构中。下面用基尔霍夫定律，求惠斯通电桥中电流计的电流IG与电源电动势及各臂电阻的关系（忽略电源的内阻）。先规定各支路电流I1，I2，I3，I4，IG及I的正方向如图3－14所示，因为节点n=4，故可列出三个节点方程，即节点A：I=I1+I2；节点B：I1=I3+IG；节点C：I3+I4=I。又因支路数P=6，故独立回路数m=P-n+1=3。选图中Ⅰ、Ⅱ、Ⅲ三个独立回路，约定其绕行方向如图3－14中箭头所示，列入回路方程。回路Ⅰ：I1R1+IGRG-I2R2=0；回路Ⅱ：I3R3-I4R4-IGRG=0；回路Ⅲ：I2R2+I4R4=ε。这样得到的6个方程联立求解得到：

 

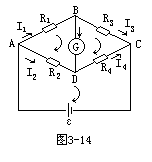
由此式可以看出，当R1/R2=R3/R4时，IG=0，当IG=0时必然有R1/R2= R3/R4。可见R1/R2=R3/R4是电桥平衡的充分必要条件。当R2R3-R1R4＞0时，IG＞0，电流IG的实际方向与图3－14中所设的正方向一致（向下）；当R2R3-R1R4＜0时，IG＜0，IG的实际方向与所设的正方向相反（向上）。

【电源】使其他形式的能量转变为电能的装置。如发电机、电池等。发电机是将机械能转变为电能；干电池、蓄电池是将化学能转变为电能；光电池是将光能转变为电能；原子电池是将原子核放射能转变为电能；在电子设备中，有时也把变换电能形式的装置，如整流器等，作为电源看待。

【电压】静电场或电路中两点间的电势差（电位差）。实用单位为伏特简称为伏或写为“Ｖ”。在交流电路中，电压有瞬时值、平均值和有效值之分。交流电压的有效值有时就简称电压。例如电力系统的输电电压有220，000伏特和330，000伏特等，工业用电电压为380伏特，照明用电的电压为220伏特都是指电压的有效值。

【绝缘体】在外电场作用下不容易传导电流的物体叫做“绝缘体”也称为非导体（电介质）。如松香、陶瓷玻璃、电木、橡皮、石蜡、塑料等都是绝缘体。绝缘体之所以导电能力弱是由于它的分子中正负电荷束缚得很紧（形成一对对的束缚电荷），在一般条件下不能相互分离，因而在其内部能作自由运动的电荷极少，电导率约在10-8S/m以下，S/m为西门子/米。

【太阳能电池】把太阳能直接转变为电能的装置。一般是在电子型硅单晶的小片上用扩散法或离子注入法渗入一薄层的硼或磷，以得到p－n结，再加上电极而成。当光照射到薄层表面时，两极间就产生电动势，一些小型电器如计算器等用灯光照射即可工作，但主要还是用太阳光做为能源，因此也称为“日光电池”或“阳光电池”。可用作人造卫星上仪表的电源。除硅外，化合物半导体砷化镓等也是制作太阳能电池的好材料。

【原子电池】将原子核放射能直接转变为电能的装置。常用的一种其结构与太阳能电池相类似，利用辐射到半导体上的带电粒子能量，使内部部分束缚电子受激发而导电，从而送出电能。有的原子电池则利用带电粒子在两电极间的定向运动，来产生通过外电路的电流。

【电子论】根据物质是电荷系所构成，亦即物质电结构的假设以解释各种物理现象的理论。经典电子论认为：当金属内部没有电场时，自由电子的无规则运动类似于理想气体分子的无规则热运动，因此金属中自由电子的整体常又称为电子气。电子在热运动过程中经常与金属骨架碰撞并改变运动方向，其轨迹是一条不规则的曲折的折线，洛伦兹用经

是一个很大的速率，但由于热运动的无规则性，从宏观上看，单位时间内通过金属中任一面元的电量为零，因此宏观电流处处为零。当金属内部存在电场时，每个自由电子都将在原有热运动的基础上附加一个逆场强方向的定向运动，正是这个定向运动而构成电流。这时每个电子的速度可以分为两个部分——热运动速度和定向运动速度。虽然定向运动的

观效应时，所有电子热运动的平均效果为零，而所有电子的定向运动由

着电流密度的数值和方向。在词目“闭合电路欧姆定律”中的微观解释就是用电子论的观点解释和推导的。经典电子论是1885年由洛伦兹首先提出的，所以也称为“洛伦兹电子论”。它也把电磁波经过物质时所呈现的各种宏观现象，归结为电磁波与物质中在准弹性力作用下的电子相互作用的结果。这一理论能够解释物质中一系列电磁现象，以及物质在电磁场中运动的一些效应，获得了相当的成功。经典电子论后来为相对论和量子论所扩充，成为现代物理学的基础。

【自由电子】对于金属原子来说，它的最外层的电子受到原子核的束缚比较弱，当这些原子组成金属导体时，一个原子的最外层电子由于受其他原子的影响，不再束缚在某个原子核周围运动，而是在整块金属中“自由”地运动着。这些电子就是金属导体中的自由电子。以常见的金属铜为例，假定每个铜原子在组成导体时，最外层有一个电子成为自由电子，则在一立方厘米的金属铜里，大约就有1023个自由电子。所以，金属中的自由电子的数目是非常可观的。金属导线中的电流正是导线中的自由电子在外加电压的作用下作定向运动的结果。由于历史上的原因通常将正电荷运动的方向规定为电流的方向。在金属导线中，既然电流是带负电的自由电子定向运动的结果，因此其电流的方向正好与自由电子的漂移运动方向相反。

【量子理论】探索微观粒子运动所遵从的量子规律的初步理论。量子力学的先驱，是从普朗克在物理学中引入量子概念开始，特别是在玻尔提出氢原子理论以后发展起来的。量子论仍然以经典物理规律为基础，但加上了一些反映微观运动具有量子特性的附加条件（量子条件）。它指出，在物体大、运动范围广（相当于量子数量很大）的极限情形下，微观运动规律应该趋近于宏观运动规律；并且两种运动规律应该具有相互对应关系（对应原理）。量子论能够解释一些简单的原子、分子所发射的光谱和黑体辐射等现象，但由于它的半经典性质，其结果在数量方面往往不能与实验符合。量子论本身还包含着很大矛盾，在解释许多实验事实时都遇到严重困难。它的进一步发展导致量子力学的建立（1924～1926年），现在这一理论虽然被量子力学所代替，故有时称之为旧量子论。但由于它直观性强，它的部分方法在解释某些现象（如复杂的光谱）时，还常被采用。人们有时也把研究微观运动的整个学科系统称为量子论或量子物理学。

【电解质】在水溶液中或在熔融状态下能导电的化合物，如酸类、碱类和盐类等。因为电解质能离解成离子，故能寻电。一般依据电离度的大小，可分为强电解质和弱电解质。

【液体导电】由电解质在溶液中离解出的正负离子导电是液体导电的特点（不包括液态金属）。例如，硫酸铜分子在通常情况下是电中性的，但它在溶液里受水分子的作用就会离解成带正电的铜离子（Cu2+）

因。当极板没有和外接电源相联时，铜离子和硫酸根离子与水分子一起在作杂乱的热运动，因而其总电流等于零。但当与一直流电源接通后，

加了一个定向的漂移运动。铜离子向负极运动；硫酸根离子向正极运动。这样溶液内发生了电荷沿一定方向的迁移，即形成了电流。由于在溶液中有两种电荷沿相反方向运动，所以在液体内的电流应是正负离子电流的绝对值总和。由此往往错误地认为，在到达正负极板上离子数都等于N时，液体中任一截面所通过的正负离子总数为2N，因而液体内通过电流，将是外电路通过电流的两倍。其实不然，假设在t时间内液体中正负离子迁移总数为2N，由于均匀分布，则取中央面为界，两边各具有相等的

离子无须通过中央截面而移向极板，到达一块极板的正或负的离子总数也是N个。通过电解溶任一截面正、负离子的总数和到达一块极板上正或负的离子总数是相同的。故电解液内所通过的电流强度和外电路通过的电流强度是相等的。

【电解】在电解质溶液或熔液电解质中通入电流，则在两个电极上（或电极旁）同时产生化学反应的过程叫作“电解”。通电时，溶液或熔体中的正离子向阴极迁移，负离子向阳极迁移；同时，在阴极上起还原反应，产生新物质；在阳极上起氧化反应，产生新物质。决定产生何种新物质的因素甚多，主要为所用电极及电解质的性质、溶液的浓度等等。例如，用炭极电解浓的食盐溶液，阴极上放出氢气，极旁产生苛性钠，阳极上放出氯气。如用炭极电解淡的食盐溶液，阴极上仍放出氢气，极旁产生苛性钠，阳性上则放出氧气而在极旁产生盐酸。又如用白金极电解硫酸铜溶液，阴极上析出铜，阳极上放出氧气，极旁产生硫酸。

【法拉第电解定律】这是英国物理学家法拉第在1933年所发现的两条电解定律：（1）电解时在电极上析出或溶解的物质的质量和电流强度，通电时间成正比，或在电极上析出的物质的质量和通过电解液的总电荷量成正比。这就是法拉第电解第一定律。它说明在电极上分离出来的物质质量m和电流强度I以及通电时间t的乘积成正比。即m∝It

m=kIt＝KQ

式中Q为析出质量为m的物质所需要的电量。K为电化当量，电化当量的数值随着被析出的物质种类而不同。某种物质的电化当量在数值上等于通过1库仑电量时析出的该种物质的质量。其单位为千克/库。（2）物质的电化当量K和它的化学当量成正比，就叫做“法拉第电解第二定律”。某种物质的化学当量是该物质的摩尔质量M（克原子量）

它的数值等于在电极上析出 1克当量物质时，通过电解质电量的库仑数。F=96500库/摩尔对于任何物质都相同。将两个定律联立可得：

【电镀】 利用电解作用，在物件之表面镀以一层金属以防止生锈，并使部件美观的加工工艺。电镀时以被镀之物件作为阴极，并以欲镀金属的盐或酸溶液为电解质，通以电流则溶液分解，金属附着于物体表面。阳极为欲镀金属逐渐被溶解，以保持溶液的浓度一定。用这种方法可以将各种金属镀在物体表面，如金、银、镍、铬等金属，不易生锈又比较光亮，所以很多机件和生活日用品往往都是电镀件。电镀时析出的金属皆为结晶体，晶体越细越均匀越好。在通常电镀工艺中的注意之点有：（1）电镀时电镀液里的金属离子浓度越低越好。而液体中的金属盐浓度则大些为宜；（2）要有适当的添加剂，添加少量的明胶等胶状物质。此种物质与金属共同被阴极吸收，可使被电镀的金属结晶变小；（3）电流密度不宜过大，因为电流密度小时结晶核的生成较迟，故结晶的成长甚佳，电镀比较均匀。电流密度过大结晶核多，各部分离子浓度不均匀，以致发生树脂状海绵状等；（4）要搅拌使电镀液均匀，以得到平滑的电镀；（5）温度要适当高一点，因为温度高可以使电镀液浓度增高，因而减少含氢现象；（6）酸性不宜过强，否则生氢而妨碍电镀（7）电镀前应把金属件的锉痕、生锈或油污等弄平滑和清洗干净，再行电镀。

【气体导电】 在通常情况下气体分子是电中性的，但在地面放射性元素的辐照以及紫外线和宇宙射线等的作用下，或多或少总有一些气体分子或原子被电离，即原来是电中性的气体分子或原子分离为一个电子和一个带正电的离子。此外，在有些灯管内，通电的灯丝也会发射电子。当在灯管两端的电极间加上一定的电压时，外加电压迫使这些电子和正离子各向阳极和阴极运动，不过此时灯管内的正离子和电子为数甚少，故所形成的电流十分微弱，在通常情况下可以忽略不计。但是，若灯管中的气体相当稀薄但不是真空，灯管两端电极上加的电压足够高，则电子在向阳极运动的过程中可以得到很大的动能，它们和中性气体相碰撞时，可以使中性分子电离，即所谓碰撞电离。同时，在正离子向阴极运动时，由于以很大的速度撞到阴极上，还可能从阴极表面上打出电子来，这种现象称为二次电子发射。碰撞电离和二次电子发射使气体中在很短的时间内出现了大量的电子和正离子。在外电压作用下这些电子和正离子向相反的方向运动。气体中就有了电流通过。常见的气体放电灯，如日光灯、霓虹灯、高压汞灯、氙灯等的灯管中都充有一定量的气体，当两端加上一定电压时，在气体中就有电流流过。在常压下的气体是不易导电的，像空气就是很好的绝缘物质，一般情况下是不导电的。使这些气体由不导电变为导电的过程称为气体击穿。雷雨时天空中的闪电就是空气被击穿形成的。通常情况气体导电是在稀薄气体中发生。常压气体不易导电，在比较高的真空中因为电子和离子不易碰到中性粒子，故也不能发生气体电流。上述的气体电离导电均属自激放电。但只靠这种碰撞电离不能长久维持自激放电，因为碰撞产生的所有电子都要向阳极运动，到了阳极便停止了。要想长久地维持放电，必须使阴极不断地提供电子。一般阴极均装有能发射电子的灯丝。

【光电子】 光子与原子中的电子碰撞，可使电子脱离原子，被撞而离开原子的电子称为“光电子”。20世纪初，雷纳对这种效应作了一番有系统的实验。其结果是：（1）光电子的能量和入射线的能量无关。（2）增加辐射的强度可使光电子数目增加。（3）光电子的能量与入射光线的颜色有关，波长较短的辐射，所生光电子的能量较高。

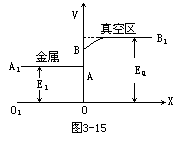
【热电子发射】 热阴极是将金属丝加热到高温（一般在2000～3000K），使金属内部的自由电子获得能量，克服金属对电子的束缚力而飞向真空空间。一个处于绝对零度的电子，从金属内部飞向真空无场空间所必须供给的最低能量，叫做功函数。不同元素具有不同的功函数。功函数用符号j表示，可写成：

j=Ea－Ei

Ei代表金属内处于绝对零度时电子可能具有的最大能量值，Ea是金属边界上的势垒高度或叫做总功函数。见图3－15所示。热阴极发射电子密度可表示为：

其中A是常数=60（安培/厘米2度2）； T为金属的绝对温度（K）； K为玻耳兹曼常数=8.62×10-5（电子伏/度）；j为金属的功函数（电子伏）。为了获得高密度的电子发射电流，阴极材料要选择熔点较高和功函数较低的材料。经常选用的有钨、钽等材料。

 

【场致电子发射】金属在强电场作用下，有电子发射现象，这种现象称为场致电子发射，或称为金属冷电子发射。场致电子发射与金属热电子发射不同。后者是由于电子跨越势垒而造成，金属冷电子发射则由于电子穿透势垒而引起。因为在阴极表面具有很强的电场，于是在真空中电子的势能曲线随着远离阴极表面而降低，如图3－16所示，图中曲线a代表电场为零的情况；b曲线代表有弱外电场的情况；c曲线代表有强外电场的情况。外电场越强，则势垒的宽度越窄。根据量子力学的观点，电子不仅具有粒子性，而且还具有波动性。并非只具有足够动能（在数值上等于功函数φ）的电子才能越过势垒高度飞出金属表面，而是具有任意动能的电子都有一定的几率穿透金属边界的势垒，进入真空空间。势垒宽度越窄，穿透的几率越大。这种现象叫做“隧道效应”。在给定条件下（外电场E，功函数φ，势垒高度等）解薛定谔方程，可得到场致发射的电流密度为

 

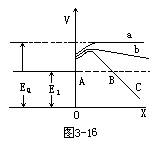
从上式可以看出，外电场E越强，功函数φ越小时，这种冷发射电流越大。场致电子发射与温度无关。

【正离子轰击发射电子】 当冷阴极放电后，就有离子在电场的加速下打到阴极，这些离子轰击阴极将会打出电子，这叫做次级电子发射。次级电子发射，是冷阴极发射电子的主要过程。如果不考虑离子复合，由冷阴极次级发射产生自持放电的稳定条件是

δN=1

这里δ是次级发射系数，即一个离子打到阴极可能打出的电子数；N是从阴极打出来的一个电子，在放电区域可能产生的离子数。显然这时放电电流应该是

Ia=I+×（1+δ）

这里的I+是打到阴极上的正离子流。

【电子枪】 电真空器件中产生聚焦电子束的电极系统。一般电子枪由三部分组成，包括热阴极、控制电极及一个或数个加速阳极。从阴极发射出的电子受各电极的静电场控制，被聚成向同一方向运动的、密集的、截面很小的电子束。也可以利用磁场使电子束聚焦，常常在真空外部加上电磁铁代替第二阳极来加强对电子束的聚焦。控制极的电压是可调的，改变控制极的电压，可以控制通过这个电极引出孔的电子数因而改变电子束的电流密度。电子枪的用途很广，像阴极射线管、示波器、电视机显象管，电子加速器等都要有发射电子的电子枪作为电子源。

【辉光放电】 在低压气体中显示辉光的放电现象。例如，在低压气体放电管中，在两极间加上足够高的电压时，或在其周围加上高频电场，就使管内的稀薄气体呈现出辉光放电现象，其特征是需要高电压而电流密度较小。辉光的部位和管内所充气体的压强有关，辉光的颜色随气体的种类而异。荧光灯、霓虹灯的发光都属于这种辉光放电。稀薄气体辉光放电的机理见辞目“气体导电”。

【弧光放电】 产生高温的气体放电现象，它能发射出耀眼的白光。通常是在常压下发生，并不需要很高的电压，而有很强的电流。例如把两根炭棒或金属棒接于电压为数十伏的电路上，先使两棒的顶端相互接触，通过强大的电流，然后使两棒分开保持不大的距离，这时电流仍能通过空隙，而使两端间维持弧形白光，称之为“电弧”。维持电弧中强大电流所需的大量离子，主要是由电极上蒸发出来的。电弧可作为强光源（如弧光灯）、紫外线源（太阳灯）或强热源（电弧炉、电焊机等）。在高压开关电器中，由于触头分开而引起电弧，有烧毁触头的危害作用，必须采取措施，使之迅速熄灭。在加速器的离子源中，也有用弧放电的源。这种弧放电机制是：电子从加热到白炽的阴极发射出来，在起弧电源的电场加速下，获得一定能量后与气体原子碰撞，产生激发与电离而引起的放电也称为“弧放电”。

【火花放电】在电势差较高的正负带电区域之间，发出闪光并发出声响的短时间气体放电现象。在放电空间内，气体分子发生电离，气体迅速而剧烈发热，发出闪光和声响。例如，当两个带电导体互相靠近到一定距离时，就会在其间发生火花和声响（它们的电势差愈大，则这种现象愈显著），结果两个导体所带的电荷几乎全部消失。实质上分立的异性电聚积至足够量时，电荷突破它们之间的绝缘体而中和的现象就是放电。而中和时发生火花的就叫“火花放电”。在阴雨天气，带电的云接近地面，由于感应作用，在云和地的中间发生火花放电即为“落雷”。由于它们之间电势差非常之大，所以这种放电的危害特别大，它可以破坏建筑物，打死人和牲畜。高大建筑物均装有避雷针就是为了对落雷的防范。在日常生活中，我们往往看到运送汽油的汽车，在它的尾部，总是有一根铁链在地上拖着走。这根铁链不是多余的而是起着很重要的作用。运汽油的车中装载的是汽油，汽车在开动的时候，里面装着汽油也不停地晃动，晃动的结果，会使汽油跟油槽的壁发生碰撞和摩擦，这样就会使油槽带电。因为汽车的轮胎是橡胶，是绝缘体，油槽里发生的电荷不可能通过轮胎传到地下，这样电荷就会积聚起来，甚至有时会发生电火花。遇到火花，汽油很容易发生爆炸。为了防止这一危险，采用拖在汽车后面的铁链来作导电工具，使产生的电荷不能积聚。

【电晕放电】带电体表面在气体或液体介质中局部放电的现象，常发生在不均匀电场中电场强度很高的区域内（例如高压导线的周围，带电体的尖端附近）。其特点为：出现与日晕相似的光层，发出嗤嗤的声音，产生臭氧、氧化氮等。电晕引起电能的损耗，并对通讯和广播发生干扰。例如，雷雨时尖端电晕放电，避雷针即用此法中和带电的云层而防止雷击。我们知道，电晕多发生在导体壳的曲率半径小的地方，因为这些地方，特别是尖端，其电荷密度很大。而在紧邻带电表面处，电场E与电荷密度σ成正比，故在导体的尖端处场强很强（即σ和E都极大）。所以在空气周围的导体电势升高时，这些尖端之处能产生电晕放电。通常均将空气视为非导体，但空气中含有少数由宇宙线照射而产生的离子，带正电的导体会吸引周围空气中的负离子而自行徐徐中和。若带电导体有尖端，该处附近空气中的电场强度E可变得很高。当离子被吸向导体时将获得很大的加速度，这些离子与空气碰撞时，将会产生大量的离子，使空气变成极易导电，同时借电晕放电而加速导体放电。因空气分子在碰撞时会发光，故电晕时在导体尖端处可见亮

【霓虹灯】 即氖灯。是一种冷阴极放电管，把直径为 12～15毫米的玻璃管弯成各种形状，管内充以数毫米汞柱压力的氖气或其他气体，每1米加约1000伏特的电压时，依管内的充气种类，或管壁所涂的荧光物质而发出各种颜色的光，多用此作为夜间的广告等。若把电容器接在霓虹灯的两极上，则可做成时亮时灭的霓虹灯广告。电容器的电容大，亮灭循环的时间长；电容器电容小，则亮灭的时间较短。霓虹灯需要电压较高。灯管越细，越长需要的电压就越高。

【日光灯】 亦称“荧光灯”。一种利用光致发光的照明用灯。灯管用圆柱形玻璃管制成，实际上是一种低气压放电管。两端装有电极，内壁涂有钨酸镁、硅酸锌等荧光物质。制造时抽去空气，充入少量水银和氩气。通电后，管内因水银蒸气放电而产生紫外线，激发荧光物质，使它发出可见光，不同发光物质产生不同颜色，常见的近似日光（荧光物质为卤磷酸钙）。荧光灯光线柔和，发光效率比白炽电灯高，其温度约在40～50℃，所耗的电功率仅为同样明亮程度的白炽灯之1/3～1/5。广泛用于生活和工厂的照明光源。

【水银灯】利用汞蒸气放电的发光灯。也称为“汞灯”。按照使用时水银气压之高低分为低压、高压与超高压水银灯。低压汞灯能辐射出较窄的汞特征谱线，在紫外线，可见光与红外线区有以下几条：（1）紫外区波长（毫微米）253.7；313.2；365.0；366.3。可见区波长（毫微米） 404.7（紫）；407.8（紫）；435.8（蓝）； 491.6（蓝绿）；546.1（绿）；577.0（黄）；579.0（黄）；612.3（红）。红外区波长（微米）1.014；1.129；1.395；1.694；1.813；1.970。这些特征谱线可用于光谱仪的波长定标。低压汞灯上在医药学上作为杀菌用灯。高压水银灯、超高压水银灯为双管构造，其内管由石英制成，直径约为2.5毫米左右，在管内封入适量的水银和氩，通电时全部水银都蒸发而能保持一定蒸气压。电极为涂上碱土金属氧化物的钨或加钍的钨。开始氩先放电，温度上升，引起水银蒸汽的放电。因气压高，原子间作用力强，因而连续光谱相当强。高压水银灯为1～3气压，超高压水银灯为10～ 200气压。高压灯各谱线的辐射强度大，可作为仪器光源，由于有相当比例的谱线是在不可见的紫外区域，若再加上一只荧光外泡后可使这部分不可见光变为可见光而作为较强的照明光源。超高压水银灯是一种体积小、亮度高、辐射很强的红外、可见及紫外光的点光源，也作为荧光显微镜、高亮度照相记录器等仪器及投影器的光源，也可作为红外光源。

【钠灯】利用钠蒸气放电的发光灯。在可见光波段辐射两条黄色谱线，其波长分别为5890×10-10米和5896×10-10米，是目前所知发光效率最高的电光源之一。用做路灯的钠灯，在夜间可产生良好的路面能见度。这种桔黄色的灯光，在雾天的透射力强而且柔和，在这种灯光下的物体，可以看得很清楚。所以不少交通要道和人工照明上，都使用钠气灯来减少汽车的交通事故。钠灯光源可以作为单色光源用于玻璃折射率测定或平面检查。发光管则以耐钠玻璃制作且封入数毫米汞柱气压的氖、钠与微量的氩。因氖的气体放电温度上升，而引起钠气压的上升，发生放电，而发出原子光谱5890×10－10米和5896×10－10米的光线。其波长在视觉敏税度最高点附近。一开始点灯时将发出氖光谱，在250℃温度附近，钠放电最大。

【氙灯】氙灯是一种高辉度的光源。它的颜色成分与日光相近故可以做天然色光源、红外线、紫外线光源、闪光灯和点光源等，应用范围很广。其构造是在石英管内封入电极，并充入高压氙气而制成的放电管。在稀有气体中，氙的原子序数大，电离电压低，容易产生高能量的连续光谱，并且因离子的能量小，电极的寿命长达数千小时。因点灯需要高电压，要使用附属的起动器、安定器、点灯装置等。使用时应当注意：（1）小心高电压注意绝缘；（2）因灯泡内有高压的氙气，小心不要过分的振动；（3）不要用眼直接看直射光；（4）灯泡要把阳极向上使用并要保持竖直；（5）固定一端另一端要呈自由状态留有热膨胀的余地；（6）因发热量很大应注意通风，必要时要实行强制通风。

【阴极射线】 在抽成1.33帕（10－2乇）以下真空的气体放电管或电子管中，由阴极发射出的电子在电场加速下所形成的电子流通称为“阴极射线”。在放电管中，阴极由于受到管内剩余气体中正离子的撞击而发射电子。在电子管中则由于受到电流的加热而发射电子。阴极射线应用很广，它能使被照射的某些物质（如硫化锌）发出荧光，而且在外加电磁场中又能迅速随着场的变化而发生偏析，电子示波器中的示波管和电视机中的显像管，均依此原理制成；在适当的电磁场中可以发散，也能够聚焦，所以也应用于电子显微镜中；高速的阴极射线照射金属板时，能产生X射线；利用电子的波动性阴极射线还可用以研究物质的结晶构造。

【汤姆逊】Thomson.Joseph John 约瑟夫·约翰·汤姆逊（1856～1940年）。英国物理学家。世界著名的卡文迪什研究所所长。1891年用法拉第管开始了原子核结构的理论研究。他研究了阴极射线在磁场和电场中的偏转,作为比值e/m（电子的电荷与质量之比）的测定，结果他从实验上发现了电子的存在。他把电子看成原子的组成部分，用原子内电子的数目和分布来解释元素的化学性质。提出了原子模型，把原子看成是一个带正电的球，电子在球内运动。他还进一步研究了原子的内部构造和阳极射线。1912年与阿斯顿共同进行阳极射线的质量分析，发现了氖的同位素。1906年他因在气体导电研究方面的成就获得了诺贝尔物理学奖。另有，威廉·汤姆逊（1824～1907年）。亦译为汤姆生。英国物理学家。1892年封为凯尔文（又译开耳芬）勋爵。在他的研究工作中，以热学和电学及它们的应用等方面最有成就。1848年创立绝对温标（亦称开氏温标）；以后，他把热力学第一定律和热力学第二定律具体应用到热学、电学和弹性现象等方面，对热力学的发展起了一定作用。此外，还制成静电计、镜式电流计、双臂电桥等很多电学仪器。1866年起，他领导完成了横越大西洋海底电缆的安装工作。1853年证明了电容放电是一种振荡。19世纪末论述了原子的构造。坚持用力学模型来解释一切物理现象。曾任格拉斯哥大学教授（1846）和校长（1904）。

【示波器】显示某些随时间变化的物理量（如电压、电流等）波形的电子仪器。一般有电子（阴极射线）示波器、脉冲示波器、电磁（磁电式）示波器三种。（1）阴极射线示波器：此种示波器为应用最广的一种示波器，用以观察变化物理量的过程，是一个阴极射线管，是显示电压波形的电子仪器。它主要由示波管、放大器、锯齿波发生器等部分组成。通过加在示波管垂直偏转板上的信号电压和加在水平偏转板上的锯齿波电压的联合控制，使电子束在荧光屏上描出所欲研究的电压波形以便观察、记录或拍摄照片。各种非电的物理量（如压力、温度等）的变动，在转换为相应的电压变动后，也可用这种示波器观察。把两个信号电压各自加在两对偏转板上，荧光屏上即显示利萨如图形（同时在两个互相垂直的方向上作谐振动的点所描出的轨迹，形状同两个谐振动的振幅之比、频率之比和周相差有关）。这样，就能由一已知信号电压的频率来测定另一个信号电压的频率或相位。阴极射线示波器不但可以用来显示波形，还可用于测量频率、相位、电压、电流，研究电子管和晶体管的特性曲线以及其它专门用途，是一种应用非常广泛的电子仪器；（2）脉冲示波器：它也是阴极射线示波器的一种，但它是研究非常短暂的和不重复的过程。例如雷电放电、绝缘体被击穿（试验时）等。显示和测量脉冲的一种宽带阴极射线示波器。它具有特殊的扫描装置，可以显示单个脉冲或一串脉冲。在雷达、电视、计算技术和核子物理等运用脉冲技术的地方，都广泛应用这种仪器；（3）电磁示波器或称光束示波器：此种示波器适于观察和记录比较缓慢的过程，例如频率在数十千周以下的振荡，一般应用电磁示波器。此种示波器，在磁场中安放一个用细丝作成的小圈，上面装有一个小镜子，过程的观察和记录就是利用这个小圈和小镜也进行的。在小圈内有电流通过时，便在磁场中转动，圈上的小镜以及由小镜反射出来的细小光束也就发生偏转。由于小圈具有这样的可动性，故其偏转以及与相随的光束偏转便重复小圈中的电流强度的变化。为了得到扫描，由小镜出来的光束射到一个转动的多面镜上，多面镜使光束以恒定的速度在另一个方向（垂直于光束因小圈振动动而发生偏转的方向）内偏转。这样一来，光束在屏上产生的亮点便画出一条曲线，此曲线便表示小圈内所通过的电流强度的变化。为了把过程记录下来，可使光束投射到感光胶片上。

【阴极射线管】利用电子束在荧光屏上聚焦，并改变其位置及强度以产生图象的电子束管。一般由电子枪、双方向偏转系统及荧光屏三部分组成。从电子枪射出的电子束在荧光屏上聚焦，产生一个很小的亮点。调节电子枪内控制电极（调制极）的电压，可改变束内电子流密度，因而改变亮点的亮度。电子束打在屏上的位置，可随偏转系统所加的电压（或电流）而移动。偏转系统有两种：一种是利用两对相互垂直的偏转板构成的静电偏转式；一种是利用两对偏转线圈构成的磁偏转式。常见的阴极射线管有示波管、电视显像管及雷达指示管等。

【示波管】它是阴极射线管的一种。在一个抽成真空的管状玻璃泡中装有一系列金属制的电极。管的一端是阴极。它的外形是一个圆筒，中间有加热用的灯丝。阴极顶部涂有发射电子效率高的金属氧化物，通常是氧化钡（BaO、氧化锶（SrO）、氧化钙（CaO）的混合物。阴极外面套有中间开小孔的圆筒状电极，称为栅极。阴极受热后发射的电子就从栅极小孔中出来。相对于阴极来说，栅极上加的是负电压。改变栅极和阴极间的负电压可以调节通过栅极小孔的电子数，所以通常又称它为“调制栅”。调制栅后面是加速极，它是一个和栅极形状相似的圆筒。加速极后面是半径略大的圆柱面状的电极，称为第一阳极。第一阳极后面还有一个半径略小的圆筒状电极，称为第二阳极。相对于阴极来说，加速极、第一阳极和第二阳极上加的都是正电压。调节这些极上的电压就可使从栅极小孔出来的电子加速，并会聚到管轴附近形成很细的一束电子流，打到管子的荧光屏上。这一段过程称为电子束的加速和聚焦。阴极、栅极、加速极、第一阳极、第二阳极这五个部分通常用镍或无磁性不锈钢制成，并由四根玻璃棒同轴地固定在一起构成一个“电子枪”，它专门发射射向荧光屏的电子束。荧光屏是一块涂有荧光物质的玻璃屏，当电子打上去时，就会发光。采用不同的荧光物质可以发出不同颜色的光，例如用钨酸钙（CaWO4）可发蓝光，用锰激活的硅酸锌（Zn2SiO4：Mn）可发绿光等。经过聚焦的电子束射到荧光屏上时，就在屏上打出一个很小的亮点。在电子枪和荧光屏之间有两组平板，相互垂直地安置着，分别称为水平和垂直偏转板。从电子枪出来的电子束在到达荧光屏之前要穿过这两组偏转板。改变加在偏转板的电压可以使电子的运动方向发生相应的变化，从而改变荧光屏上亮点的位置。从屏上亮点的轨迹可以看出加在偏转板上的电压的变化情况。从屏上反回来的电子，则通过管壁上的石墨层汇集到第二阳极而流出管外，和示波管外边的供电电路构成闭合回路，示波管中的电子流就成为整个回路电流的一个组成部分。

【半导体】 导电性能介于导体和绝缘体之间非离子性导电的物质。室温时其电阻率约为10-3～l09欧姆·厘米。一般是固体。例如锗（Ge）、硅（Si）以及一些化合物半导体。如碲化铅（PbTe）、砷化铟（InAs）、硫化铅（PbS）、碳化硅（SiC）等。与金属材料不同，半导体中杂质含量和外界条件的改变（如温度变化、受光照射等），都会使半导体的导电性能发生显著变化。纯度很高，内部结构完整的半导体，在极低的温度下几乎不导电，接近绝缘体。但随着温度的升高半导体的电阻迅速减小。含有少量杂质，内部结构不很完整的半导体通常可分为n型和p型两类。半导体的p－n结以及半导体同某些金属相接触的边界层，都具有单向导电或在光照下产生电势差的特性。利用这些特性可以制成各种器件，如半导体二极管、三极管和集成电路等。半导体之所以具有介于导体和绝缘体之间的导电性，是因为它的原子结构比较特殊，即其外层电子既不象导体那样容易挣脱其原子核的束缚，也不象绝缘体中的电子被原子核紧紧地束缚着。这就决定了它的导电性介于两者之间。

【能带】 研究固体物理学中的一种理论。虽然所有的固体都包含大量的电子，但有的具有很好的电子导电性能，有的则基本上观察不到任何电子导电性。这一基本事实曾长期得不到解释。在能带理论的基础上，首次对为什么有导体、绝缘体和半导体的区分提出了一个理论上的说明，这是能带论发展初期的重大成就。在物理学中往往形象化地用水平横线表示电子的能量值，能量越大，线的位置越高。一定能量范围内的许多能级（彼此相隔很近）形成一条带，称为“能带”。各种晶体的能带数目及其宽度等均不相同。相邻两能带间的能量范围称为“能隙”或“禁带”，晶体中的电子不能具有这种能量。完全被电子占据的能带称为“满带”，满带中的电子不会导电；没有电子占据的带称为“空带”；部分被占据的称为“导带”，导带中的电子才能导电，价电子所占据的能带称为“价带”。能量比价带低的各能带一般都是满带。价带可以是满带也可以是导带；如在金属中是导带，所以金属能导电，在绝缘体和半导体中是满带，所以它们不能导电。但半导体很容易因其中有杂质或受外界影响（如光照、加热等），使价带中的电子数减少，或使空带中出现一些电子而成为导带，因而也能导电。

【本征半导体】 不含杂质且结构非常完整的半导体单晶，其中参与导电的电子和空穴数目相等。温度极低时，其电阻率很大，极难导电；随着温度升高，电阻率急剧减小。当硅、锗等半导体材料制成单晶体时，其原子的排列就由杂乱无章的状态变成非常整齐的状态。其原子之间的距离都是相等的，约为2.35×10-4微米。每个原子最外层的4个电子，不仅受自身原子核的束缚，而且还与周围相邻的4个原子发生联系。这时，每两个相邻的原子之间都共有一对电子。电子对中的任何一个电子，一方面围绕自身原子核运动，另一方面也时常出现在相邻的原子所属的轨道上，这样的组合叫做“共价键”结构。硅、锗共价键结构的特点是它们外层共有的电子所受到的束缚力并不象在绝缘体中那样紧，在一定的温度下，由于热运动，其中少数电子还是可能挣脱束缚而成为自由电子，形成电子载流子。当共有电子在挣脱束缚成为自由电子后，同时留下了一个空位。有了这样一个空位，附近的共有电子就很容易来进行填补，从而形成共有电子的运动。这种运动，无论是效果上还是现象上，都好象一个带正电荷的空位子在移动。为了区别于自由电子的运动，就把这种运动叫做“空穴”运动，空位子叫做“空穴”。由此可见，空穴也是一种载流子。当半导体处于外加电压作用之下，通过它的电流可以看作是由自由电子的定向移动所形成的电子流，另一部分是带正电的空穴定向移动。所以半导体中，不仅有电子载流子还有空穴载流子，这是半导体导电的一个特点。这种纯单晶半导体，虽然多了一种空穴载流子，但是载流子的总数离开实际应用的要求，也就是从具有良好导电能力的要求来看，还相差很远，所以这种本征半导体的实际用处不大。

【杂质半导体】在纯单晶的本征半导体中，掺杂一些有用的杂质，使其导电特性得到很大的改善。而其导电性能取决于杂质的类型和含量。这样的半导体即称为“杂质半导体”。大多数半导体都是这一种类型。将半导体材料提纯，再用扩散或用离子注入法掺入适当的杂质，可以制成n型半导体或p型半导体。利用不同类型的杂质半导体，可以制成整流器，半导体二极管、半导体三极管和集成电路等重要部件。由此可以看到，只有杂质半导体才是最有用的。

【n型半导体】“n”表示负电的意思，在这类半导体中，参与导电的主要是带负电的电子，这些电子来自半导体中的“施主”杂质。所谓施主杂质就是掺入杂质能够提供导电电子而改变半导体的导电性能。例如，半导体锗和硅中的五价元素砷、锑、磷等原子都是施主杂质。如果在某一半导体的杂质总量中，施主杂质的数量占多数，则这种半导体就是n型半导体。如果在硅单晶中掺入五价元素砷、磷。则在硅原子和砷、磷原子组成共价键之后，磷外层的五个电子中，四个电子组成共价键，多出的一个电子受原子核束缚很小，因此很容易成为自由电子。所以这种半导体中，电子载流子的数目很多，主要靠电子导电，叫做电子半导体，简称n型半导体。

【p型半导体】“p”表示正电的意思。在这种半导体中，参与导电的主要是带正电的空穴，这些空穴来自于半导体中的“受主”杂质。所谓受主杂质就是掺入杂质能够接受半导体中的价电子，产生同数量的空穴，从而改变了半导体的导电性能。例如，半导体锗和硅中的三价元素硼、铟、镓等原子都是受主。如果某一半导体的杂质总量中，受主杂质的数量占多数，则这半导体是p型半导体。如果在单晶硅上掺入三价硼原子，则硼原子与硅原子组成共价键。由于硼原子数目比硅原子要少很多，因此整个晶体结构基本不变，只是某些位置上的硅原子被硼原子所代替。硼是三价元素，外层只有三个价电子，所以当它与硅原子组成共价键时，就自然形成了一个空穴。这样，掺入的硼杂质的每一个原子都可能提供一个空穴，从而使硅单晶中空穴载流子的数目大大增加。这种半导体内几乎没有自由电子，主要靠空穴导电，所以叫做空穴半导体，简称p型半导体。

【p－n结】在一块半导体中，掺入施主杂质，使其中一部分成为n型半导体。其余部分掺入受主杂质而成为p型半导体，当p型半导体和n型半导体这两个区域共处一体时，这两个区域之间的交界层就是p-n结。p-n结很薄，结中电子和和空穴都很少，但在靠近n型一边有带正电荷的离子，靠近p型一边有带负电荷的离子。这是因为，在p型区中空穴的浓度大，在n型区中电子的浓度大，所以把它们结合在一起时，在它们交界的地方便要发生电子和空穴的扩散运动。由于p区有大量可以移动的空穴，n区几乎没有空穴，空穴就要由p区向n区扩散。同样n区有大量的自由电子，p区几乎没有电子，所以电子就要由n区向p区扩散。随着扩散的进行，p区空穴减少，出现了一层带负电的粒子区；n区电子减少，出现了一层带正电的粒子区。结果在p－n结的边界附近形成了一个空间电荷区，p型区一边带负电荷的离子，n型区一边带正电荷的离子，因而在结中形成了很强的局部电场，方向由n区指向p区。当结上加正向电压（即p区加电源正极，n区加电源负极）时，这电场减弱，n区中的电子和p区中的空穴都容易通过，因而电流较大；当外加电压相反时，则这电场增强，只有原n区中的少数空穴和p区中的少数电子能够通过，因而电流很小。因此p－n结具有整流作用。当具有p－n结的半导体受到光照时，其中电子和空穴的数目增多，在结的局部电场作用下，p区的电子移到n区，n区的空穴移到p区，这样在结的两端就有电荷积累，形成电势差。这现象称为p－n结的光生伏特效应。由于这些特性，用p－n结可制成半导体二极管和光电池等器件。如果在p－n结上加以反向电压（n区加在电源正极，p区加在电源负极），电压在一定范围内，p－n结几乎不通过电流，但当加在p－n结上的反向电压越过某一数值时，发生电流突然增大的现象。这时p-n结被击穿。p－n结被击穿后便失去其单向导电的性能，但结并不一定损坏，此时将反向电压降低，它的性能还可以恢复。根据其内在的物理过程，p－n结击穿可分为雪崩击穿和隧道击穿两种。由于p－n结具有这种特性，一方面可以用它制造半导体二极管，使之工作在一定电压范围之内作整流器等；另方面因击穿后并不损坏而可用来制造稳压管或开关管等器件。

【晶体二极管】亦称为“半导体二极管”。一种由半导体材料制成的，具有单向导电特性的两极器件。早期的半导体二极管是用金属丝尖端触在半导体晶片上制成的，称为点接触二极管，通常在较高的频率范围内作检波、混频器用。目前大多数的晶体二极管都是面结型的，它是由半导体晶片上形成的p－n结组成，或由金属同半导体接触组成，可用于整流，检波、混频、开关和稳压等。除一般用途的二极管外，还有一些用于特殊用途，利用特殊原理制成的二极管。例如：（1）肖特基二极管（又称为金属-半导体二极管）：用某些金属和半导体相接触，在它们的交界面处便会形成一个势垒区（通常称为“表面势垒”或“肖特基势垒”），产生整流，检波作用。在这种二极管中，起导电作用的热运动能量比较大的那些载流子，所以又叫“热载流子二极管”。这种二极管比p－n结二极管有更高的使用频率和开关速度，噪声也比较低，但工作电流较小，反向耐压较低。目前它主要用作微波检波器和混频器，已在雷达接收机中代替了点接触二极管；（2）隧道二极管：它是一种具有负阻特性的半导体二极管。目前主要用掺杂浓度较高的锗或砷化镓制成。其电流和电压间的变化关系与一般半导体二极管不同。当某一个极上加正电压时，通过管的电流先将随电压的增加而很快变大，但在电压达到某一值后，忽而变小，小到一定值后又急剧变大；如果所加的电压与前相反，电流则随电压的增加而急剧变大。因为这种变化关系，只能用量子力学中的“隧道效应”加以说明，故称隧道二极管。它具有开关、振荡、放大等作用，应用在电子计算机和微波技术中；（3）变容二极管；它是利用p-n结的电容特性来实现放大、倍频、调谐等作用的一种二极管。由于它的结电容随外加电压而显著变化，所以称为“变容二极管”。制造变容二极管所用的半导体材料主要用硅和砷化镓。在作微波放大时，它的优点是具有很低的噪声；（4）雪崩二极管：亦称为“碰撞雪崩渡越时间二极管”。是一种在外加电压作用下可以产生超高频振荡的半导体二极管。它的工作原理是：利用p－n结的雪崩击穿在半导体中注入载流子，这些载流子渡越过晶片流向外电路。由于这一渡越需要一定的时间，因而使电流相对于电压出现一个时间延迟，适当控制渡越时间，在电流和电压的关系上会出现负阻效应，因而能够产生振荡。雪崩二极管主要用在微波领域作为振荡源；（5）发光二极管：一种在外加正向电压作用下可以发光的二极管。它的发光原理是：在正向电压作用下，p－n结中注入很多非平衡载流子，这些载流子复合时，多余的能量转化为光的形式发射出来。发光二极管经常用作电子设备中的指示灯、数码管等显示元件，也可用于光通讯。它的优点是工作电压低，耗电量小体积小、寿命长。制造发光二极管所用的半导体材料主要是磷砷化镓、碳化硅等。

 

【晶体三极管】 亦称为“半导体三极管”或简称“晶体管”。它是一种具有三个电极，能起放大、振荡或开关等作用的半导体器件。按工作原理不同，可分为结型晶体管和场效应晶体管。结型晶体管是在半导体单晶上制备两个p－n结，组成一个p－n－p（或n－p－n）的结构，中间的n型（或p型）区叫基区，边上两个区域分别叫发射区和集电区，这三部分都有电极与外电路联接，分别称为“发射极”以字母e表示、“基极”以字母b表示和“集电极”以字母c表示。在电子线路中，用符号代表p－n－p型和n－p－n型晶体管如图3－17所示。晶体管用作放大器时，在发射极和基极之间输入电信号，以其电流控制集电极和基极（或集电极和发射极）之间的电流，从而在负载上获得放大的电信号。同电子管相比晶体管具有体积小、重量轻、耐震动、寿命长，耗电小的优点，但受温度影响较大。目前常用的晶体管主要是用锗或硅晶体制成。场效应晶体管是利用输入电压的电场作用控制输出电流的一种半导体器件。场效应晶体管又分为结型场效应晶体管和金属—氧化物—半导体场效应晶体管两大类。金属—氧化物—半导体场效应晶体管简称为MOS晶体管，它的结构如图3－18所示，其中1为栅极；2为绝缘层；3为沟道；4为源；5为漏。制作过程为在n型（或p型）晶片上扩散生成两个p型（或n型）区，分别称为源和漏，从上面引出源极（接电压正端）和漏极（接负端），源和漏之间有一个沟道区，在它上面隔一层氧化层（或其它绝缘层）制作一层金属电极称为“栅极”。在场效应晶体管工作时，栅极电压的变化会引起沟道导电性能的变化，也就是说栅极电压变化控制了源漏之间的电流变化。场效应晶体管的特点是输入阻抗高和抗辐射能力强。

 

【集成电路】 它是一种微型电子器件或部件。是采用一定的工艺，把一个电路中所需要的晶体管、电阻、电容和电感等，制作在一小块或几小块晶片或陶瓷基片上，再用适当的方法进行互连而封装在一个管壳内，成为具有所需功能的微型电路结构。集成电路已打破了传统的电路设计概念，因为集成电路中的晶体管、二极管、电阻、电容、电感等各元件在结构上已组成一个整体，这样整个电路的体积大大缩小，且引出线和焊接点的数目也大大减少，从而使电子元件向着微小型化，低功耗和高可靠性方面迈进了一大步。用集成电路来装配电子设备，其装配密度比用分立式晶体管等元器件组装的电子设备提高几十倍到上百倍，设备的稳定工作时间也可大大提高。因此集成电路在电子计算机、通讯设备、导弹、雷达、人造卫星和各种遥控、遥测设备中占据了非常重要的地位。根据制造工艺的不同，目前集成电路主要有半导体集成电路、薄膜集成电路、厚膜集成电路和混合集成电路等几类。根据性能和用途的不同，又可分为数字集成电路、线性集成电路和微波集成电路等。近年来集成电路的发展极为迅速。早期半导体集成电路的集成度是每个晶片上只有几十个元件，目前集成度已高达每片包含几千个甚至上万个元件。习惯把由一百个以上的门电路或一千个以上的晶体管集成在一块晶片上，并互连成具有一个系统或一个分系统功能的电路称为“大规模集成电路”。

【半导体集成电路】 亦称“固体电路”或“单块集成电路”，它是在一块半导体单晶片（一般是硅片）上，用氧化、扩散或离子注入，光刻、蒸发等工艺做成晶体管、二极管、电阻和电容等元件，并用某种隔离技术使它们在电性能上互相绝缘，而在晶片表面用金属薄膜使有关元件按需要互相连接，最后被封装在一个管壳里而构成一个完整电路。半导体集成电路制造方法比较简便，成本低廉、可靠性高、体积也比较小，是目前集成电路中生产和应用最多的一种。

【磁性】能够吸引铁、钴、镍等物质的属性叫做“磁性”。古代就已发现一种称为“磁石”的天然矿石（Fe3O4）具有磁性。我国古代四大发明之一的指南针即利用磁石制成。后来发现，磁体和电流之间，电流和电流之间也具有相斥相吸的作用，因而逐步确定了磁和电有密切的联系。磁性起源于电流或实物内部电荷（电子、原子核）的运动。

【磁学】研究物质磁性及其应用的学科。它以电子论和统计物理学为基础来阐明物质的抗磁性、顺磁性和铁磁性。由于物质的磁性起源于物质内部电子和核子的运动，而且它们的运动都遵从量子规律和量子统计法，现代磁学的研究同量子理论密切有关。在这基础上，磁学又有了很大的发展。目前已从电磁学中分出而成为独立的科学。

【永磁体】 永磁体有天然磁体和人造磁体两种。天然磁体是直接从自然界得到的磁性矿石。人造磁体通常是用钢或某些合金，通过磁化、充磁制成的。永磁体是能够长期保持磁性的磁体。永磁体可以制成各种形状，常见的有条形磁铁、针形磁铁和马蹄形磁铁。永磁铁用处很多，如在各种电表，扬声器、耳机、录音机、永磁发电机等设备中都需要永磁体。

【磁极】磁体上磁性最强的部分。针形、条形、马蹄形磁铁的磁极，都是接近两端处。若将条形磁铁置于铁屑中，取出后会观察到磁铁的两端吸引的铁屑最多。若将一个条形磁铁悬挂起来，使它可以在水平面内自由转动，静止时它将沿南北方向取向；指北的一端称北（N）极，指南的一端称南（S）极。磁体的同名极相斥，异名极相吸。在任何一个磁体上，南极和北极总是成对出现，而且它们的强度相等。若将一条磁棒分为两段，每段磁棒均有一对N、S极，且无论将磁棒分为多少段，其每小段必存在N极和S极。这说明磁体不存在独立的N极或S极，两极总是相伴而生的。表示磁极强弱的物理量称为“磁极强度”简称“磁强”。两个强弱相同的磁极，在真空中相距1厘米时，如果它们之间相互作用力为1达因，则每个磁极的强度就规定为一个电磁系单位制的磁极强度单位。

【磁化】使原来不显磁性的物体在磁场中获得磁性的过程称为“磁化”。最容易磁化的铁磁性物质，如软铁、硅钢等。由于电流能够引起很强的磁场，且便于控制，所以常利用电流产生的磁场使铁磁性物质磁化而制成永久磁铁或电磁铁。若用磁铁的N极靠近铁棒，则靠近磁铁的一端磁化为S极，远离磁铁的另一端为N极，即靠近磁铁一端的极性与磁铁该端的极性恰好相反。如果被磁化的物质是软铁，当磁化磁场撤消后，铁的磁性几乎全部消失这种类型的材料称之为软磁材料。制造电磁铁必须用软磁材料这样才能通过电流控制磁铁的磁力。若被磁化的是碳素钢，则当磁化磁场撤消后，钢仍然有磁性，说明钢能保持磁性，这类材料称之为硬磁材料。故常用碳素钢制造永磁体。

【磁力】磁场对电流、运动电荷和磁体的作用力。电流在磁场中所受的力由安培定律确定。运动电荷在磁场中所受的力就是洛伦兹力。但实际上磁体的磁性由分子电流所引起，所以磁极所受的磁力归根结底仍然是磁场对电流的作用力。这是磁力作用的本质。

【磁场】在永磁体或电流周围所发生的力场，即凡是磁力所能达到的空间，或磁力作用的范围，叫做磁场；所以严格说来，磁场是没有一定界限的，只有强弱之分。与任何力场一样，磁场是能量的一种形式，它将一个物体的作用传递给另一物体。磁场的存在表现在它的各个不同的作用中，最容易观察的是对场内所放置磁针的作用，力作用于磁针，使该针向一定方向旋转。自由旋转磁针在某一地方所处的方位表示磁场在该处的方向，即每一点的磁场方向都是朝着磁针的北极端所指的方向。如果我们想象有许许多多的小磁针，则这些小磁针将沿磁力线而排列，所谓的磁力线是在每一点上的方向都与此点的磁场方向相同。磁力线始于北极而终于南极，磁力线在磁极附近较密，故磁极附近的磁场最强。磁场的第二个作用便是对运动中的电荷所产生的力，此力恒与磁场及电

量度。

【磁场强度】表示磁场强弱和方向的矢量。由于磁场是电流或运动电荷引起的，而磁介质在磁场中发生的磁化对磁场也有影响。因此磁场强度有两种表示法：在充满均匀磁介质的情况下，包括介质因磁化而产

在磁场中所受的力（参见“洛伦兹力”）。磁场强度则与产生磁场的电

的比值为介质的磁导率μ。磁感应强度的电磁系单位为特斯拉。磁场强

的磁感应强度与磁场强度之间的重要关系。一般各向同性非铁磁质的μ

小成正比。其μ叫做磁介质的绝对磁导率，是描写磁介质性质的宏观标量点函数。

【磁力线】描写磁场分布情况的曲线。这些曲线上各点的切线方向，就是该点的磁场方向。曲线越密的地方表示磁场强，曲线稀的地方表示磁场弱。磁力线永远是闭合的曲线，永磁体的磁力线，可以认为是由N极开始，终止于S极。实际上永磁体的磁性起源于电子和原子核的运动，与电流的磁场没有本质上的区别，磁极只是一个抽象的概念，在考虑到永磁体内部的磁场时，磁力线仍然是闭合的。

【磁通量】表征磁介质（或真空）中磁场分布情况的物理量。通过磁场中任何一面积元S的磁通量等于磁感应强度矢量在该面积之法线方向上的分量与面积的乘积，即Φ=BnS=BScosθ，其中θ为面元的法线与磁感应强度的夹角。θ=90°，cosθ=0，Φ=0这时磁场方向与面元平行。θ=0°，cosθ=1，Φ=BS这时磁场方向与面元垂直。在国际单位制中磁通量的单位为韦伯。在电磁感应现象中，感生电动势的大小取决于磁通量的变化率。

【地球磁场】是由地球本身具有磁性，而在其周围形成的磁场。它的两极接近于地球两极，但并不完全重合。两者之间的偏差还随着时间有所变化。指南针在静止时沿地球南北方向取向，这表明地球是一个大磁体。地球磁体的N极（北极）位于其地理南极附近。地球磁体的S极（南极）位于地理北极附近。指南针正是借助于地球是个大磁体和利用磁的相互作用规律而制成的。

【磁偏角】地磁场强度矢量所在的垂直平面与地理子午面之间的夹角。不同地点的磁偏角一般是不同的，同一地点的磁偏角也因时而变。磁子午线北端在真子午线以东为东偏，以西为西偏；一般规定东偏为正，西偏为负，指南针就是一个磁偏角指针。它不但能指出各地磁偏角每日的微小变化，也能显示在较长时间内所发生的较强的变化。如 1649年，

1890年又减至约11度偏西。各地磁偏角资料，为航海者必不可少。航海者使用的一种特殊地图上标有各地磁偏角，图上磁偏角相等的地方均用线连接起来，即所谓“等偏线”。等偏线极不规则，其线路与地理子午线全不相合。

【磁倾角】地球表面任何一点的地磁场总强度矢量和水平面之间的夹角。地磁场强度方向在水平面之下的，磁倾角定义为正；在水平面之上的，磁倾角为负。

【磁感应强度】 描写磁场强弱和方向的物理量。它的数值反映该点磁场的强弱，它的方向为该点的磁场方向。磁感应强度的大小为：当

行于磁场方向运动时，受力为零）。对不同电量（q＞0），以不同的速度在垂直于磁场的方向通过某p，得到各自不同的F⊥，但其F⊥与乘积qv之比相同。即

式中的F⊥i表示qi以垂直于磁场方向的速度v⊥i通过P点时所受到的磁场力。可见比值F⊥/qv⊥是一个与运动电荷无关的量。在磁场中的不同点，这个比值一般不相同，但对场中一确定点，它是一个确定值。可见这个比值反映了该点磁场的特性。在电磁学上定义这一比值为磁感

B为该点磁感应强度的数值。它反映了该点磁场的强弱。磁场力总是

 

【磁现象的本质】丹麦科学家奥斯特于 1820年发现电流的磁效应，第一次揭示了磁与电存在着联系，从而把电学和磁学联系起来。为了解释永磁和磁化现象，安培提出了分子电流假说。安培认为，任何物质的分子中都存在着环形电流，称为分子电流，而分子电流相当一个基元磁体。当物质在宏观上不存在磁性时，这些分子电流做的取向是无规则的，它们对外界所产生的磁效应互相抵消，故使整个物体不显磁性。在外磁场作用下，等效于基元磁体的各个分子电流将倾向于沿外磁场方向取向，而使物体显示磁性。安培的假说还说明了磁体的N、S两种磁极不能单独存在的原因，因为基元磁体的两个极对应于环形电流所在平面的两个侧面，显然这两个侧面是不能单独存在的。近代物理表明：原子核外电子除绕核运动外，电子自身还有自旋。分子、原子等微观粒子内这些电子的运动均构成等效的分子电流。按照近代的观点，电荷在（不论其运动与否）其周围激发电场。而运动电荷（电流）在其周围激发磁场。与电场是一种特殊的物质一样，磁场也是一种特殊物质，在磁场中的运动电荷（电流）受到该磁场给予的作用力（磁场力）。电流I1和I2之间的相互作用，是I1的磁场给其场中的电流I2以作用；反过来I2的磁场又给其场中电流I1以作用。电流之间的相互作用是通过磁场来传递的。永磁体之间的磁现象，来源于永磁体中分子电流所激发的磁场和磁场给永磁体内分电流的作用力。

【毕奥—萨伐尔定律】简称毕萨定律，说明电流元与其所产生的场的磁感应强度关系的定律，其数学表示式为

电流元IdL的磁场的磁感应线。若以右手握电流元，姆指伸直代表电流

的μ0为毕萨定律在MKSA（国际单位）制中所具有的系数，μ0=4π×10ˉ7（韦伯/安培·米）或（牛顿/安培2）。式中其它各量的单位分别为I——安培，r、dl——米，B——特斯拉。和电场一样，磁感应强

场的出发点。

 

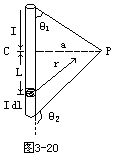
【直线电流的磁场】图3－20所示为一载流直长导线，设其电流

律可知，电流元Idl在P点的元磁感应强度为

矢量和归结为一个线积分即

积分要遍及整个直线。先把被积函数化为θ的函数，设

OC=L，则：

L=-actgθ

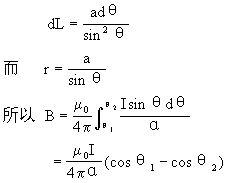
式中θ1，θ2分别为直导线两端的电流元与其到场点的矢径的夹角。如果导线为无限长，则θ1=0，θ2=π，则

【安培力】它是指磁场对电流的作用力。一段通电直导线放在磁场中，通电导线所受力的大小和导线的长度l、导线中的电流强度I、磁感应强度B以及电流方向和磁场方向之间的夹角θ的正弦成正比。安培力F=KLIBsinθ。该力的方向一般用左手定则，也可用右手螺旋法则来确定。这一规律只在匀强磁场中适用。因为只有匀强磁场中的各点的磁

用。当导线的长度、导线中的电流强度、磁感应强度的单位都采用国际单位米、安培、特斯拉时，比例常数K=1。两条平行通电直导线间的作用力，可应用安培力的公式计算。通有电流I1的直线导线在距其为

放一根同相平行的通电流I2的直导线，那么，它所受的安培力为

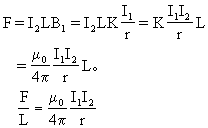
电流乘积成正比，和它们之间的距离成反比，其方向由左手定则而定。左手定则，是伸开左手使拇指和其余四指成垂直并且在同一平面上，让四指指向电流的方向，而磁场方向由手心穿过，这时拇指所指方向，便是安培力的方向。

【安培】Ampere，Andre－Marie（1775～1836年）。 1775年元月 22日生于法国里昂附近的波勒米。1801年在布尔学院教授物理学和化学。他最大的贡献是电磁学，首先发现两平行电流同向流动则互相吸引，异向流动则互相排斥。他还发现了电磁学的基本定律之一，即安培定律。他以数学理论描述这一现象，成为发展电动力学的基础。为了纪念他，以安培为电流的国际单位制基本单位。安培单位的定义为：处于真空中相距1米的两无限长而圆截面积可忽略的平行直导线内，通过恒定电流时，当两导线之间产生的力在每米长度上等于2×10-7牛顿时，则其电流强度为1安培。

【电流天平】又称安培秤。用以通过测量F来确定电流I。如图3－21所示。在图的右下方有两个被固定在天平底座不能移动的固定线圈A和B。在A、B之间放置一悬吊在天平右臂砝码盘上的可以移动的活动线圈C。在线圈通电流以前，在左边砝码盘上加适当砝码使与活动线圈平衡。然后将电流I引入线圈C中，并使A、B、C均通以相同的电流I，但B、C线圈的电流有相同流向，而A、C线圈的电流有相反向。因而B线圈对动线圈C是相吸的而A线圈对C则是相斥的，其合力是将动线圈C垂直拉向下方。在左边砝码盘上添加砝码，使天平重新平衡，从而测得载流线圈之间的作用力F。从而可由安培力公式，即

 

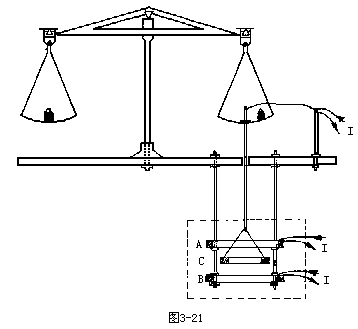
注意到 μ0=4π×10－7

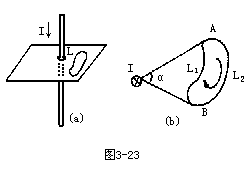
【安培定律】“安培环路定律”的简称。这个定律指出在磁场中磁

电流的倍，其数学表示式为

上述关系称为安培环路定理。在闭合曲线包围一载流直导线如图3－22a所示。在垂直于通电导线的平面上取一包围导线的闭合曲线L如

位矢，于是有

 

所以

则

所以

 

如果闭合曲线不包围载流直导线，如图3－23a所示。图3－23b中，纸面为直导线垂直的平面，曲线L为平面上电流I之外的任意闭合曲线。由I作闭合曲线L的切线，切点分别为A、B，点A、B将闭合

注意到在L1段中有cosθ＜0所以

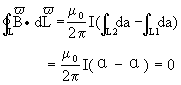
多根载流导线时则有

我们所熟悉的安培定则（右手螺旋定则），则是指出磁场环流的方向与通电电流方向的关系。

 

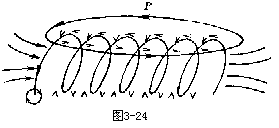
【螺线管】 用导线沿着圆筒侧面绕成的螺旋形线圈。它就是最原始的电磁铁，设螺线管远比其直径长。螺线管的磁场为其每匝所产生磁场的矢量和。从图3－24所示情况可以看出，如果螺线管的匝间间隔较大，显示导线之间的磁场有相抵消之势，并显示在螺线管外距导线较远之点P的磁场与螺线管平行，在线管内的中央附近地带的磁场也与其轴平行。在导线紧密绕制的极限情况下，螺线筒实际上变为筒状电流层。当螺线管很长时（当趋于无限长时），其筒状电流层在管外各点的磁场趋近于零。如果实际螺线管的长度远大于直径，在远离两端时取外部磁场为零是可以的。整个螺线管外部磁场要比其内部磁场弱得多。应用安培定律

积分之和，则

 

右边第一个积分为Bh，h为路径a至b的长度。路径ab虽与管轴

电流I与螺线 管内的电流I0不同，因为积分路径所包围的不止一匝。令n为单位长度之匝数，则

I=I0（nh）

安培定律即变为

Bh＝μ0I0nh

B=μ0I0n

虽然上式是就无限长之理想螺线管推导而来的，但对实际螺线管靠近中央内部诸点而言是适用的。它说明磁感应强度B与螺线管的直径或长度无关，且在螺线管截面上的B不变。为得到实验用的给定的匀强磁场，用螺线管为可行的方法，就像欲产生已知之匀强电场用平行板电容器为可行的方法一样。

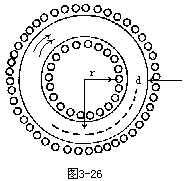
【螺线环】图3－26所示为一螺线环，此环可看成一有限长度之

如图所示。再对半径为r的圆路径应用安培定律：

即  B·2πr=μ0I0N

I0为螺线环内的电流强度，N为总匝数。由此得

由于r选的不同、B也不同。因此B在螺线环截面内并非不变，此点与螺线管不同。由安培定律也可以证明，在理想的螺线环外各点的磁感应强B度等于零。证明从略。

 

 

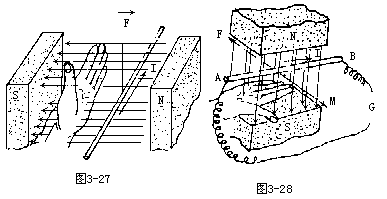
【左右手定则】左手定则亦称“电动机定则”。它是确定通电导体在外磁场中受力方向的定则。其方法是：伸开左手，使拇指与其余四指垂直，并都与手掌在同一平面上。设想将左手放入磁场中，使磁力线垂直地进入手心，其余四指指向电流方向，这时拇指所指的方向就是磁场对电流作用力的方向如图3－27所示。右手定则亦称“发电机定则”。确定导体在磁场中运动时导体中感生电流方向的定则。伸开石手，使拇指与其余四指垂直，并都和手掌在同一平面内。假想将右手放入磁场中，让磁力线垂直地从手心进入，使拇指指向导体运动的方向，这时其余四指所指的方向就是感生电流的方向。如图3－28所示

 

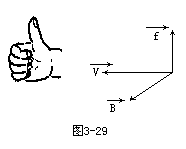
【右手螺旋定则】表示右手螺旋柄的旋转方向和螺旋前进方向之间相互关系的定则。例如在笛卡儿右手坐标系中，以从x轴经过90°转到y轴的方向为旋转柄旋转方向，z轴就沿着旋转的前进方向。又如用矢量表示角速度时，如果转动的方向沿着螺旋柄旋转方向，螺旋的前进

者之间的方向关系可用右手螺旋定则来描述：握紧右手，伸直拇指，当

所示。确定通电导体在外磁场中受力方向的左手定则，也可以用右手螺

四指垂直的拇指的指向就是导体受到的磁场力的方向。

【洛仑兹力】运动电荷在磁场中所受的力，它和电荷的电量、磁感应强度、电荷运动的速度及两者之间的夹角的正弦成正比，方向由左手定则确定。用右手螺旋法则也可确定。有时也把只受磁场部分的力称为“洛仑磁力”。由实验我们知道磁场施于运动中的电荷的磁力恒与电荷的运动方向和磁场方向所确定的平面相垂直。假设运动电荷在电磁场中

积，即

Fm=qVBsinθ

电磁场中受的电场力为Fe，则它所受的电场力为，

运动电荷在电磁场中所受的洛仑兹力F为

基本公式。磁场力的一个重要特征是，无论磁场中运动电荷的速度V怎样，洛仑兹力 总是与 垂直，因而磁场力对运动电荷不作功：

· =0（FVcosθ中的cosθ=0）

磁场力只改变运动电荷速度的方向，而不改变其速率数值。

【洛仑兹】Lorentz，Hendrik Antoon（1853～1928年）荷兰物理学家。创立经典电子论，对经典电磁理论有一定贡献。确定了电子在电磁场中所受的力（洛仑兹力），并预言了正常的塞曼效应。为了解释迈克耳孙—莫雷实验的结果，提出了在以太中运动的物体在运动方向上缩短的假说，因与爱尔兰物理学家斐兹杰惹同时提出，称为洛仑兹—斐兹杰惹收缩；并在以太学说的基础上提出高速运动的参考系与静止参考系之间时间、空间坐标的变换形式，后被称为洛仑兹变换。这些工作与相对论的建立有关。

【电荷的圆周运动】设一质量为m，电量为q的粒以速度 沿垂直于磁场方向进入一匀强磁场 中，图 3－ 30所示，其中q=-e（即电子）， 垂直进入纸面。因为 =q × ， 只改变速度的方向，而不改变速度的数值，因而作用在运动电荷上的力 的大小恒定不变。其次， ⊥ 并且 、 均在垂直于 的纸平面内。由力学知识可知，这是一个向心力，F向=qVB，故带电粒子作位于纸平面内的匀速圆周运动。

 

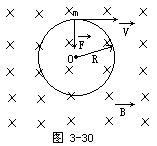
因为F向=qVB

q／m为带电粒子的电量与其质量之比，叫荷质比。由此可见，荷质比（q／m）一定的带电粒子在匀强磁场中作圆运动时，不论其速度有多大，其角速度均相同，因而这些粒子在相同的时间内转过相同的角度，故必有相同的周期T。而周期为

说明荷质比相同的粒子，当其在匀强磁场中作垂直于 的运动时，其圆运动的周期T和频率f与速度无关。这是因为粒子的速度增大时，其圆运动的半径也正比地增大。带电粒子运动的这些特点具有重要的实际意义。回旋加速器、磁聚焦理论都要用到这一结论。注意，在同一磁场中，正、负带电粒子圆周运动的转动方向相反。

 

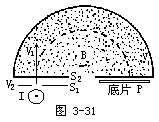
【质谱仪】是一种分析各种同位素并测量其质量及含量百分比的仪器。当一束带电的原子核通过质谱仪中的电场和磁场时，凡其荷质比不相等的，便被分开。图3－31为质谱仪的示意图。图中I为离子源，S1和S2为两个狭缝，从离子源引出的离子受到施于S1及S2间的电位差，在通过S1到S2的路径上被加速，成为具有一定速度的离子束，进入磁感应强度为 的匀强磁场区。进入磁场时的速度由下式

决定。正离子在这一磁场中运动时其轨道如图中所示半径为r的圆。当离子走过一半圆而抵达照相底片P时会在它上面留下痕迹。由轨道半径r=mv／qB（见洛仑兹力），得

合并（1）、（2）式，消去v，即得

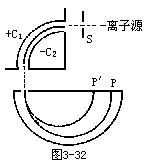
因为V、B及r可直接测量得到，所以如果我们能够用其他方法决定离子所带的电荷q，，则由上式便可求出离子的质量。我们可以用质谱仪将电荷相同而质量不同的离子分开。科学家应用这种仪器在1920年左右发现了同种化学元素的原子其质量可以不相同；这些质量不同的同一种元素的原子被称为同位素。汤姆逊首先利用电磁场测定电子的荷质比的原理，同样可运用到带正电的离子，从荷质比很容易算出该离子的质量。正离子通常带电量等于一个电子（称为单电荷离子）。但有时也带有两个、三个甚至四个电子电量（称为多电荷离子）。目前应用的质谱仪是非常精确的仪器，它不但可以测量出每种同位素之准确质量，并可测定每种同位素在元素中所占的百分比。如将这种仪器略加修改，也可应用到同位素分离。质谱仪的形式很多，但所应用的主要原理及结构却大同小异。图3－32所示是一台现代用质谱仪的主要装置部分。这装置是在真空中，正离子流自离子源引出经过窄隙S进入一圆形之电场C1C2，调节C1C2之间的电压，可选择一定能量之正离子，这些正离子随着电场之形状弯曲90°而进入一个半圆形的匀强磁场中，磁场的方向与图面垂直且指向纸内，进入磁场之正离子受磁力作用而沿半圆形轨道进行。因正离子e／m之大小不同，轨道形成大小不等的半圆。分别落在底片上的不同位置也就是说元素将按其质量大小的顺序而排列，故称之为“质谱”。如果我们分别测出每种粒子的电流。就能从这些电流大小的比例中，得出该种在离子源中被电离的物质的各种同位素的成分比例。它也可以把化合物中的不同物质的离子分开进行成分分析。

 

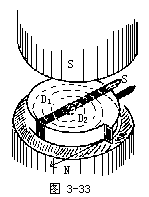
【回旋加速器】回旋加速器是用于加速质子、氘核、α粒子（氦的原子核）等使之获得高能量的装置。它是核物理研究的重要工具。图3－33为回旋加速器的示意图。D1、D2为装于同一水平面上的半圆形中空铜盒（又称D形盒）。两盒间留有一定宽度的间隙，置于真空中。由大型电磁铁产生的匀强磁场B垂直于D形盒。由高频振荡器产生的交变电压加于两D形盒间，这个电压将在两盒空隙间产生电场以加速带电粒了，而盒内由于电屏蔽效应其电场强度趋近于零。在加速器中心有离子源。产生的离子通过离子源的引出孔而进入回旋加速器中。假设此时D2正好处于高电位，则离子将被两D形盒间的电场加速而进入D1盒中。D1盒中不存在电场，但却存在由电磁铁产生的匀强磁场。因而离子以不变的速率在D1盒中作匀速圆周

（见词目“电荷的圆周运动”）是确定值，它与速度v和半径r的数值无

振荡电源的周期T0=T，这时两D形盒的电位差的方向与前者相反，D1处于高电位状态。离子在D形盒空隙中再次被加速获得新的能量。按相

中，如此不断，直至被加速到所需的能量。由于离子圆运动半

最后当被加速离子趋于D形盒的边缘时，借助于一个有静电电势的偏转板可以控制粒子的运动，使粒子打在内靶或外靶上。假如 D形盒的半径

为RD，则RD是离子作圆周运动的最大半径，此时离子速率值最大。

 

这就是回旋加速器径加速后离子所获得的最大动能。回旋加速器的优点在于以不很高的振荡电压对离子不断加速而得到高能离子流。若采用一次加速以获得如此能量，其加速电压U必定很高，

设回旋加速器半径RD=0.48（米），B=1.8（韦伯／米2），

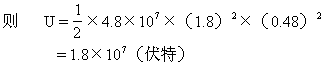
即RD=0.48（米），B=1.8（特斯拉）的回旋加速器所获得的氘核能量，等效于直线加速器具有一千八百万伏特加速电压

c为光速。而回旋加速器必须满足f0=f（或T0=T）的条件，而

当m随v增大而增大时，f（粒子旋转频率）必然随之减小。若f0恒定，则破坏了f0=f的条件，甚至可能起到减速粒子的作用。若使电子和氘核具有相同能量，由于电子质量远小于氘核，其速度就应远大于氘核，它将很快受到上述相对论效应的限制。因而回旋加速器一般用来加速较大质量的粒子，而不用以加速电子。加速电子可利用“电子感应加速器”。

【电子感应加速器】电子感应加速器是回旋式加速器的一种，它是利用变化的磁场而激发的感生电场而达到加速电子的目的。在圆形电磁铁的两极间，有一环形真空室，在交变电流激励下，两极间出现交变磁场，这交变磁场又激发一感生电场。从电子枪射到真空室的电子受到两个作用力：（1）受感生电场沿切向的加速力；（2）受磁场沿径向的洛仑兹力，充当维持圆周运动的向心力。

【磁流体发电机】 当热游离气体很快地通过磁场时，如果磁场很强，将很快把热游离气体中的正、负带电粒子在洛仑兹力的作用下分别集聚在流体管道两侧的两个极上，这样将热能直接转变为电能，而不需要锅炉或涡轮发电机，这种发电装置称为“磁流体发电机”，简称MHD，MHD需要很强的磁场，一般只有超导磁铁才能做到。此外，MHD管子本身并不是一个完全的发电机，电浆离开管子后，还要经过压缩、加热、再回到管子，才完成一个循环，所以必须发展能耐高温的材料，才能更进一步地改良MHD。同时此材料必须能在极高的温度下，具有抗碱金属腐蚀之特性，这给人们带来了材料方面的难题，当此问题解决后，MHD将能以极高的效率，供给可靠的电流。

【电磁感应】通过闭合回路面的磁通量发生变化而产生电动势的现象。这样产生的电动势称为“感应电动势”。这一现象首先由法拉第于1831年发现的。磁通量的变化在线圈中产生的电流，称为“感应电流”。感应电流的产生可用导体中自由电子受到磁场的洛仑兹力来说明。麦克斯韦认为磁场变化时，即使导体不存在，也将引起电场，因而在任何闭合路径中形成电动势。电磁感应现象继奥斯特实验（电流引起磁场）之后进一步揭示了磁现象和电现象之间的紧密依存关系。麦克斯韦方程组以此为主要依据之一。在电机工程中，也有很重大应用，例如发电机、变压器等都是以电磁感应现象为根据而制成的。若一导线在1秒钟内切割1韦伯的磁感应通量时，此导线两端可产生1伏特的感应电动势。欲使感应电动势增强，可采取如下的方法：（1）加快导线与磁场相对运动之速度；（2）加强磁感应强度；（3）将单根直导线加长，或用多根单直导线单向同时切割磁力线后串联起来；（4）采用最大的切割磁力线的角度（即重直切割）。在无数的实验中证明，只要在闭合线圈中磁通有变化就会出现感应电流，不管这个变化是由什么原因引起的。它可以是磁场与线圈的相对运动，也可以是电流的变化所引起的。

【楞次】LenZ，Heinrich Friedrich EmiL（1804～1865年）1804年2月12日生于俄国爱沙尼亚，最初攻读神学，后转学习物理学。1834年任圣彼得堡大学（后为列宁格勒大学）教授，俄国科学院院士。1834年发表楞次定律，说明了感应电流的方向。1835～1838年又找出电阻和温度的关系。

 

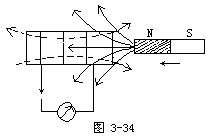
【楞次定律】当导线在磁场中运动时，或磁场在线圈中变化时，由导线上感应电流的磁效应所形成的另一磁场作用，在反抗导线或磁铁与原有磁场间的相对运动。即感应电流的方向为阻止磁场的变化方向，也就是感生电流的磁通总是力图阻碍引起感生电流的磁通变化，这就是“楞次定律”。应该注意，楞次定律是判断感应电动势方向的定律，它是通过感应电流的方向来表述的。按照这个定律，感应电流必定采取这样一个方向，使得它所激发的磁通阻碍引起它的磁通变化。所谓阻碍一个磁通的变化是指：当磁通增加时，感应电流激发的磁通与原来磁通方向相反（阻碍它的增加）；当磁通减小时，感应电流的磁通与原来磁通方向相同（阻碍它的减小）。按照上述的情况可以确定被感生电流所激发的磁场的方向，在根据右手螺旋法则，可知线圈或螺线管中的感应电流的方向。楞次定律实际是能量守恒定律在电磁感应现象中的反映。为了理解这点，可从功和能的角度分析。比如，当磁铁插入线圈时，线圈出现感应电流。按照楞次定律，感应电流所激发的磁感应线的方向如图3－34中虚线所示。如果把这个线圈看作磁铁，其右端相当于N极，它正好与向左插入的N极相斥。为使磁铁匀速向左插入（强调匀速是使其动能不变，否则分析时还要考虑动能变化），必须借助于外力克服这个斥力做功。另一方面，感应电流流过线圈及电流计时必然要发热，这个热量正是外力作功转化而来的。可见楞次定律符合能量守恒和转化这一普遍规律。设想感应电流的方向与楞次定律的结论相反，图3－34线圈的右端就相当于S极，它与向左插入的磁铁左端的N极相吸，磁铁在这个吸引力的作用下将加速向左运动（无需其它向左的外力），线圈的感应电流越来越大，线圈与磁铁的吸力也就越来越强。如此下去，一方面磁铁的动能越来越大，另一方面是感生电流放出越来越多的焦耳热，而在这一过程中竟没有任何外力做功，这显然是违反能量守恒定律的。可见，能量守恒定律要求感应电动势的方向遵循楞次定律。再如。图3－35中abcda是一个闭合电路（简称线框），“×”表示外加恒定均匀磁场 的方向指向纸面里边、线框的磁通Φ等于B与线框所围面积S的乘积。当可动边ab在外力作用下向右平移时，线框面积增加。由楞次定律可知感应电流I的方向为逆时针，如图中箭头所示。从功和能的角度分析。载有感应电流的导体段。ab既然处在磁场之中，自然受到磁场的作用力（安培力）。应用左手定则这个力向左，因此它是ab段导线向右平移的阻力。

 

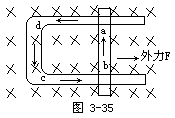
为使ab边向右匀速平移，就要用外力克服这个阻力做功，正是这个功转化为感应电流放出的焦耳热。如果感应电流的方向与楞次定律的结论相反，ab边所受的安培力不是阻力而是动力，这显然也要导致违反能量守恒定律的结论。由此楞次定律也可以描述为：当导体在磁场中运动时，导体中由于出现感应电流而受到的磁场力（安培力）必然阻碍此导体的运动。这可以称为楞次定律的第二种表述。楞次定律的两种表述有一个共同之点，就是感应电流的后果总与引起感应电流的原因对抗。在第一种表述中，“原因”指引起感应电流的磁通变化，“后果”指感应电流激发的磁通。在第二种表述中，“原因”指导体的运动，“后果”则指导体由于其中出现感应电流而受到的安培力。

【感应电流】未接入电流的闭合导线，受外加变化磁场影响而产生的电流称为“感应电流”或“感生电流”。一般产生感应电流的方法有三种：（1）移动邻近导线的磁铁。（2）变化邻近导线电路中的电流。（3）移动邻近通有电流的导线电路。根据楞次定律，感应电流的方向为反对产生磁通量变化的方向。

【感应电动势】因磁通量ΦB的改变而产生的电动势，称为感应电动势。其大小与磁通量的变化量成正比例。

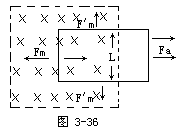
如图3－36，设某人施力 a，使导线以速度 向右作等速直线运动，因有感应电流I产生，则导线上所受的磁力 m=IL 。导线作等速运动

∴ a=- m

施力 a在△t时间内所作的功

W=P△t＝（Fαv）△t

=（-Fmv）△t= -ILBv△t

在△t时间内，通过此电路任一点的电荷为I△t，推动此电荷所需的能量为

qU=εI△t

依照能量不灭定律及△t时间内长L的导线所扫过的面积Lv△t

W=-ILBv△t＝εI△t

感应电动势的方向，恒使回路产生一感应电流，此感应电流产生一感应

表示感心电动势所产生感应磁通量之方向，即反抗原有磁通量变化的方向。

 

【法拉第电磁感应定律】当穿过回路的磁通量发生变化时，回路中的感生电动势ε感的大小和穿过回路的磁通量变化率

这就是法拉第电磁感应定律，这个定律清楚地表明，决定感应电动势的大小不是磁通Φ本身而是磁通随时间的变化率dΦ／dt，当磁铁插在线圈内部不动时，线圈的磁通虽然很大，但并不随时间而变化，故仍然没有感应电动势及感应电流。法拉第定律使我们能够根据磁通的变化率直接确定感应电动势。至于感应电流，则还要知道闭合电路的电阻才能求得。在更复杂的情况下，电路中还可能接有其他电源，确定电流时还必须考虑到它们的影响。此外如果线路并不闭合（或说电阻为无限大），则虽有感生电动势却没有感生电流。可见，在理解电磁感应现象时，感应电动势是比感应电流更为本质的东西。只是由于感应电流比感应电动势易于显示，所以法拉第在这个方面的第一个实验是通过感应电流发现电磁感应现象的。象其他一些科学家一样，法拉第起先也做过许多实验，企图发现恒定电流在其附近的闭合线圈中“感应”出电流来，但都遭到失败。然而；他不放过实验中的每一个细节，终于在一次实验中注意到在一个电路中电流接通和切断的瞬间，其附近的闭合线圈内出现了一短暂的感应电流。由此他敏锐地意识到：电路接通或切断时的电流变化之所以在其附近线圈引起感应电流，很可能是由于它使该线圈的磁通发生变化所致。如果令电路的电流不变但与线圈作相对运动，也有希望在线圈中引起感应电流。他沿着这一思路反复实验，终于取得了伟大成果。在国际单位制中，ε的单位为伏特，Φ的单位为韦伯，t的单位为秒，这时，实验测得的K=1，故法拉第定律此时的形式为

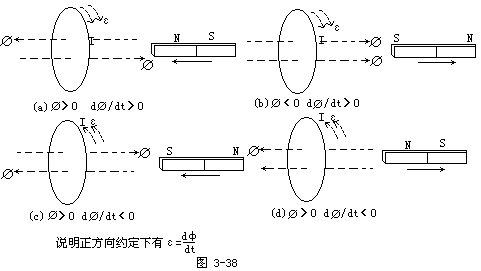
此式确定了感生电动势的大小，其方向由楞次定律确定。为了在运算中不但考虑到电动势的大小而且考虑到它的方向，最好把这两个定律统一表述为一个数学式子。为此，必须把磁通Φ和感生电动势ε看成代数量，并对它们的正负赋予确切的含义，要给代数量的正负赋予意义就要事先给它约定一个“正方向”。当实际方向与正方向相同时，该量数值为正（＞0），否则为负（＜0）。各量正方向均可任意约定，但同一定律对不同正方向可有不同的表达式（差别在于式中的正负号）。当约定感应电动势ε与磁通Φ的正方向互成右手螺旋关系时，如图3－37所示，考虑到楞次定律后法拉第定律应写成

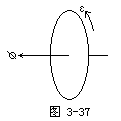
式中负号正是楞次定律在这种正方向约定下的体现。证明的方法是把所 方向与楞次定律一致。可能情况有下列四种：（1）Φ＞0且

dΦ/dt＞O（图 3－ 38a）。Φ＞0说明磁通实际方向与图3－37的正方向相同，即向左，如图3－38a的虚箭头Φ所示（按习惯，在必须同时画出正方向和实际方向时，正方向以实箭头表示，实际方向以虚箭头表示）。dΦ／dt＞表明这个向左的磁通绝对值随时间增

际方向与图3-37的正方向相反，如图3－38a的虚线箭头ε所示。由ε的实际方向可得感应电流I的实际方向（与ε相同），故I激发的磁通Φ′向右。既然Φ本身向左而且在增加，向右的Φ′自然是阻碍Φ的变化，

（2）Φ＜0且dΦ／dt＞0（图3－38b）。Φ＜0说明磁通实际方

但两Φ都小于零，故后一时刻的｜Φ｜小于前一时刻的｜Φ｜。可见Φ＜0及dΦ／dt＞0合起来表明Φ的绝对值在减小。

向右既然Φ向右且绝对值在减小，向右的Φ′就是阻碍原磁通减小。可

且dΦ／dt＜0（图3-38c）。（4）Φ＞0且dΦ／dt＜0（图3－

结论与楞次定律一致。对Φ=0且dΦ／dt＞0或Φ=0且dΦ／dt＜0，

这时ε＜0，即感生电流产生的磁场和原磁场方向相向；当磁通量减少

场和原磁场方向相同。要注意，在中学阶段，物理量的大小和方向常常

其方向由楞次定律或右手定则来确定。

 

【动生电动势】只要闭合电路的磁通有变化就有感应电动势，并不问这种变化的起因。事实上，磁通是磁感应强度 对某一曲面的通量，磁通变化的原因无非是：（1）B不随时间变化（恒定磁场）而闭合电路的整体或局部在运动。这样产生的感应电动势叫做“动生电动势”。（2） 随时间变化而且闭合电路的任一部分都不动。这样产生的感应电动势叫做“感生电动势”。（3） 随时间变化且闭合电路也有运动。这时的感应电动势是动生电动势和感生电动势的迭加。

【动生电动势与洛仑兹力】法拉第定律作为一个整体是一个实验定律，但其中的一部分，即 不变而闭合电路运动所引起的动生电动势所服从的规律，却可由理论推导。电荷在磁场中运动时要受到洛仑兹力，这正是动生电动势产生的原因。设图3－39中导线ab以速度v向右平移，它里面的电子也随之向右运动。由于线框处在外加磁场中，向右运动的电子就要受到洛仑兹力。根据洛仑兹力的公式

其中e是电子电量绝对值，可知 向下，它促使自由电子向下运动，闭合线框中便出现逆时针方向的电流。产生这个电流的动生电动势存在于ab段中，因此运动着的ab段可看成一个电源，其非静电力就是洛仑兹力。反过来，我们从洛仑兹力出发，则因为 与 垂直，所以每个电子所受的洛仑兹力（绝对值）

f=evB

单位正电荷所受洛仑兹力（绝对值）

动生电动势（绝对值）

式中l是导线ab的长度，v是ab在单位时间内移动的距离，故vl是它在单位时间内所扫过的面积，即线框abcda的面积的变化量，于是vBl便是线框的磁通在单位时间的变化量，即磁通变化率dΦ／dl，可见

这与法拉第定律一致，另外根据洛仑兹力的方向判断出的动生电动势方向也与楞次定律一致。以上虽然是从一个特例证明了由洛仑兹力可以推出关于动生电动势的法拉第定律（及楞次定律）。可以证明，这个结论对任意形状的闭合导线在任意恒定磁场中作任意运动造成的动生电动势都成立。这就表明，关于动生电动势的法拉第定律是洛仑兹力公式的必然结果。因此，一般情况下的动生电动势可由下式计算：

积分遍及整条导线。若为闭合导线，上式结果与法拉第定律结果相同；若为非闭合导线，法拉第定律不能直接使用（因Φ对非闭合曲线无意义），但上式仍然成立。

 

【磁场中的带电粒子】当带电粒子束以速度v进入使它偏转的匀强磁场区B时，将受磁场力f=qvB（当 与B垂直时）=mv2／r，所以

设电子束偏转的夹角为θ，偏转量为D，偏转磁场中心到荧光屏距离为L，

从该式中得知磁偏转量D和电子速率的一次方成反比，而电偏转量将和

向上）。在加速电压高，电子速率大的情况下，采用磁偏转比较合适。如果被偏转的是某种带正电的离子，则偏转方向将与电子的偏转方向相反。又因离子总比电子质量大很多，就是质量最小的氢离子（H+）（即质子）的质量也是电子质量1840倍。所以离子偏转要比电子小得多。

 

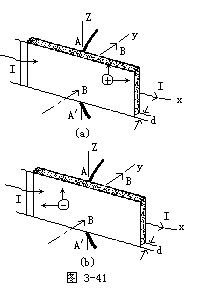
【霍耳效应】当电流垂直于外磁场方向通过导体时，在垂直于电流和磁场的方向的导体两侧产生电势差的现象。电势差的大小与电流和磁场强度的乘积成正比，而与物体沿磁场方向的厚度成反比。比例系数称霍耳系数，它同物体中载流子的符号和浓度有关。一般说来，金属和电解质的霍耳效应都很小，但半导体则较显著。因此，研究固体的霍耳效应可以确定它的导电类型以及其中载流子的浓度等；利用半导体的霍耳效应可以制成测量磁场强度的磁强计、微波技术及电子计算机中的元件等。如图3－41a所示，有一个厚度为d、宽为l的导电薄片，沿x轴通有电流强度I。当在y轴方向加以匀强磁场B时，在导体薄片两侧（图中的A，A′）产生电势差UAA′。这就是霍耳效应。假设所讨论导电薄片的载流子（参与导电的带电粒子）电量为q。若q＞0时，其它向漂移速度 。薄片中这些正电荷的载流子在磁场 中将受到洛仑兹力f洛=+|q| × 。由图3－41a可知，这些正电荷的载流子所得到的力沿+Z轴方向。若薄片中载流子为负电荷，q＜0，则其定向漂移速度 ′与 的方向相反、受的洛仑兹力fL=-|q| ′× 。虽然此力前有负号，但 ′与 方向相反，所以fk也沿+Z轴方向见图3－41b。可见，由于 的存在，定向运动的载流子（无论q＞0或q＜0）都将受到+Z轴方向的洛仑兹力

f1=qvB

设载流子为正电荷，由于洛仑兹力的作用，正电荷将在A侧堆积，而在A′侧出现负电荷，并产生由A指向A′的横向电场Et。显然Et对q的作用力fe=qE，与fL=qvB反向，当

或当电场Et满足

Et=vB

时，定向运动的载流子所受合力为零。这时载流子将回到与磁场 不存在时相同的运动状态，同时A，A′两侧停止电荷的继续堆积，从而在AA′两侧建立一个稳定的电势差UAA

所以UAA′＝vBL

又电流强度I=nqvL·d，n为单位体积的载流子数。则载流子的漂移速度

v=I／nqLd

将其代入UAA′=vBl得

若载流子为负电荷，作与前相同的讨论，仍然得到上式，不过式中q＜0，因而UAA′＜0即A′点的电势高于A点。只要我们将式中的q理解为

k称为霍耳系数，与所测材料的物理性质有关。当载流子q＞0时，k＞0，所以UAA＞0；当q＜0时，k＜0，所以UAA′＜0，由

流子浓度n，以及载流子的电性能（q＞0或q＜0）。霍耳效应广泛应用于半导体材料的测试和研究中。例如用霍耳效应以确定一种半导体材料是电子型（n型——多数载流子为电子）还是“空穴”型（p型——多数载流子为空穴）。半导体内载流子的浓度受温度、杂质以及其它因素的影响很大，因此霍耳效应为研究半导体载流子的浓度的变化提供了

而对双原子价的金属以及半导体材料，霍耳系数不能写成这种形式，必须用量子理论来说明。但半导体材料的霍耳系数k与其载流子浓度n之间仍有反比关系。利用霍耳效应的霍耳元件有很多方面的用途：例如测量磁场；测量直流和交流电路中的电流强度和功率；转换信号，如把直流电流转换成交流电流并对它进行调制，放大直流或交流讯号等。

 

【磁单极子】一种尚未发现的基本粒子。狄拉克在1931年将电磁场加以量子化，同时预测磁单极的存在。在指出磁单极所带的磁荷必须是hc／e的整数倍（正或负）。磁单极的存在可用以解释为何一切粒子的电荷总是e的整数倍（正或负）。一切已知的磁性物质都有两个磁极，但“磁单极”却是只有一个磁极的物质。

【电动机】 电动机也称为“马达”，把电能转变为机械能的机器。利用电动机可以把发电机所产生的大量电能，应用到生产事业中去。构造和发电机基本上一样，原理却正好相反，电动机是通电于转子线圈以引起运动，而发电机则是借转子在磁场中之运动产生电流。为了获得强大的磁场起见，不论电动机还是发电机，都以使用电磁铁为宜。电动机因输入的电流不同，可分为直流电动机与交流电动机：（1）直流电动机——用直流电流来转动的电动机叫直流电动机。因磁场电路与电枢电路连结之方式不同，又可分为串激电动机、分激电动机、复激电动机；（2）交流电动机——用交流电流来转动的电动机叫交流电动机。种类较多，主要有：①整流电动机——使串激直流发电机，作交流电动机用，即成此种电动机，因交流电在磁场与电枢电路中，同时转向，故力偶矩之方向恒保持不变，该机乃转动不停。此种电动机因兼可使用交、直流，故又称“通用电动机”。吸尘器、缝纫机及其他家用电器等多用此种电动机。②同步电动机——电枢自一极转至次一极，恰与通入电流之转向同周期的电动机。此种电动机不能自己开动，必须用另一电动机或特殊辅助绕线使到达适当的频率后，始可接通交流电。倘若负载改变而使转速改变时，转速即与交流电频率不合，足使其步调紊乱，趋于停止或引起损坏。因限制多，故应用不广。③感应电动机——置转子于转动磁场中，因涡电流的作用，使转子转动的装置。转动磁场并不是用机械方法造成的，而是以交流电通于数对电磁铁中，使其磁极性质循环改变，可看作为转动磁场。通常多采用三相感应电动机（具有三对磁极）。直流电动机的运动恰与直流发电机相反，在发电机里，感生电流是由感生电动势形成的，所以它们是同方向的。在电动机里电流是由外电源供给的感生电动势的方向和电枢电流I方向相反。交流电动机中的感应电动机，其强大的感应电流（涡流）产生于转动磁场中，转子上的铜棒对磁力线的连续切割，依楞次定律，此感应电流有反抗磁场与转子发生相对运动的效应，故转子乃随磁场而转动。不过此转子转动速度没有磁场变换之速度高，否则磁力线将不能为铜棒所切割。

【电动机的反电动势】由电动机的转子切割磁力线而产生，其方向与外加电压相反，故称为“反电动势”。此时通过电枢线圈的电流，正比于外加电压与反电动势之差。设V为外加电压，ε为反电动势，R为直流电动机之内电阻，则通过直流电动机的电流：

V=ε＋IR

电动机在开始起动时，反电动势极小，故通入的电流很大。为避免将转子烧坏，可于电路中串联一个变阻器，当电机从启动到正常运转时其电阻逐渐减小，最后到达一个正常值。大型电动机中之启动器，就是此种装置。因直流电动机在开始转动时，反电动势极小，转子内有很大电流，因而能发出很强的转动力，因此电车推动器常用此种直流电动机。在电流通过电解槽时，由于电极或电解质发生化学变化，也有反电动势发生。

 

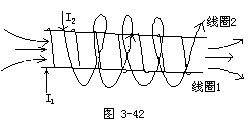
【自感】电路中因自身电流变化而引起感应电动势的现象。在具有铁心的线圈中特别显著。如果在原线圈中通有电流，当电流发生变化时，不仅仅是付线圈因此而产生感生电动势，而且原线圈本身也造成自感电动势，有时这种电动势也被称为反电动势，因为它总是反抗本身电流的变化，这种现象在只有一个线圈的情况下，也是如此。如图3－42所示，线圈1和线圈2分别流有电流且电流随时间缓慢地改变，则穿过任何线圈的磁通量，除了由另外线圈所产生的以外，尚需考虑到自身的磁通量。故在线圈2的感生电动势，可被写成

同理线圈1的感生电动势除了决定于线圈2之电流变化，也决定于自身电流的改变，即

如果只有一个线圈，则只剩下自感电动势

L被称为自感，由线圈的几何性质而定。

【自感系数】自感系数也叫做电感，或直接称为线圈的自感，常以符号L代表，是用来表示各种电器用具（如线圈）在自感现象方面之特性的一个物理量。线圈的自感系数，就是用在线圈中电流强度每秒改变1安培时所产生的自感电动势来表示的。自感系数的单位为：当导体中电流强度每秒钟改变1安培时，若产生的自感电动势为1伏特，那么这导体的自感系数，就是1“亨利”。

【自感电动势】 沿导体流通的电流在导体周围建立起磁场，这个磁场穿过此导体所连成的电路。当导体中的电流强度发生变化时，穿过回路的磁通量就发生变化，由于电磁感应现象，回路中就有电动势发生，这就是所谓的自感电动势。这个电动势永远与产生这个电动势的电流变化方向相反（楞次定律）。即当电流增大时，自感电动势的方向和电路中电流方向相反；而在电流减小时，和电流流通的方向相同。由于这个缘故，当电路中有电流发生时，自感电动势作负功（因为它的方向与电流相反）。相反，当电路中电流消逝时，自感电动势作正功（因为它的方向与电流方向相同）。

【互感】由于一个电路中电流变化，而在邻近另一个电路中引起感生电动势的现象。也就是相互感应，是两个电路间磁力的相互作用。如果两个电路的位置排列得使一个电路内的电流所产生的磁场能够贯穿另一个电路，则第一个电路内电流强度的变化会使这个磁场发生变化，而由于电磁感应现象，也就使第二个电路内发生了电动势。第一个电路的磁场贯穿第二个电路的部分越大，则两个电路之间的互感越强。如果线圈1与线圈2共轴地套在一起。当线圈1输入电流时，它所建立的磁场亦包含在线圈2内，因此线圈1磁通量的变化即等于线圈2内的变化。如果线圈1之螺线管长为L，总圈数为N1，横截面积为A；线圈2总圈数为N2，当线圈1输入缓变电流I1，则线圈2之感应电动势为

互感的实用单位为亨利，即

相反地，如果电流输入线圈2，则在线圈1的电动势即利用线圈2建立的磁场，计算线圈1之磁通量变化率，线圈1的感应电动势也与线圈2之电流变化率成正比，故

对任意两线圈总有M12=M21，简记作M。 M叫做两线圈间的互感系数（简称互感），它表征两线圈间互感耦合的强弱。互感系数与自感系数有相同的单位。可以证明，与自感系数类似，互感系数也只取决于两线圈的几何因素（形状、大小、匝数、互相配置等）及磁介质的特性而与电流无关（有铁心时除外）。互感在电工电子学技术中应用很广，变压器就是一个重要例子。变压器中有两个匝数不同的线圈，由于互感耦合，当在一个线圈两端加上交流电压时，另一个线圈两端将感应出数值不同的电压。但变压器不能用来变换直流电压，因为线圈在直流电压作用下出现直流电流，其磁场不随时间变化，故另一线圈不会出现感生电动势（因而不会出现电压）。在实验室中，为了方便地从低压直流电源获得很高的电压，可以使用感应圈。感应圈由套在同一铁心上的两个匝数是悬殊的线圈及一个断续器构成，有无断续器是感应圈与变压器的主要差别所在。由于断续器的作用，原线圈1在接通直流电源时将出现变化电流，从而在副线圈2中感生出很高的电动势。互感现象在某些情况下也要带来不利的影响。在电子仪器中，元件之间不希望存在的互感耦合会使仪器工作质量下降甚至无法工作。在这种情况下就要减少互感耦合，例如把容易产生不利的互感耦合的元件远离或调整方向以及采用“磁场屏蔽”的措施等。

【涡流】“涡电流”的简称，也称为“傅科电流”。迅速变化的磁场在导体（包括半导体内，引起的感应电流，其流动的路线呈涡旋形，故称“涡流”。磁场变化越快，感应电动势越大，因而涡流也就越强。涡流能使导体发热。在磁场发生变化的装置中，往往把导体分成一组相互绝缘的薄片（如变压器的铁心）或一束细条（如感应圈的铁心），以减低涡流强度，从而减少能量损耗。但在需要产生高温时，又可利用涡流来取得热量，如高频电炉就是根据这一原理设计的。这种金属内部出现的涡流，是由于电磁感应情况下的洛仑兹力或感生电场力在整块金属内部引起的感应电流。涡流流动情况可用电流密度 描述，由于多数金属的电阻率很小，因此不大的感应电动势往往可以在整块金属内部激起强大的涡流。当一个铁心线圈通过交变电流时在铁心内部激起涡流。它和普通电流一样要放出焦耳热。利用涡流的热效应进行加热的方法叫做感应加热。冶炼金属用的高频感应炉就是感应加热的一个重要例子。当线圈通入高频交变电流时，在线圈中的坩埚里的被冶炼金属内出现强大的涡流，它所产生的热量可使金属很快熔化。这种冶炼方法的最大优点之一，就是冶炼所需的热量直接来自被冶炼金属本身，因此可达极高的温度并有快速和高效的特点。此外，这种冶炼方法易于控制温度，并能避免有害杂质混入被冶炼的金属中，因此适于冶炼特种合金和特种钢等。涡流的热效应对变压器和电机的运行极为不利。首先，它会导致铁心温度升高，从而危及线圈绝缘材料的寿命，严重时可使绝缘材料当即烧毁。其次，涡流发热要损耗额外的能量（叫做“涡流损耗”）使变压器和电机的效率降低。为了减小涡流，变压器和电机的铁心都不用整块钢铁而用很薄的硅钢片迭压而成。

【趋肤效应】亦称为“集肤效应”。交变电流通过导体时，由于感应作用引起导体截面上电流分布不均匀，愈近导体表面电流密度越大。这种现象称“趋肤效应”。趋肤效应使导体的有效电阻增加。频率越高，趋肤效应越显著。当频率很高的电流通过导线时，可以认为电流只在导线表面上很薄的一层中流过，这等效于导线的截面减小，电阻增大。既然导线的中心部分几乎没有电流通过，就可以把这中心部分除去以节约材料。因此，在高频电路中可以采用空心导线代替实心导线。此外，为了削弱趋肤效应，在高频电路中也往往使用多股相互绝缘细导线编织成束来代替同样截面积的粗导线，这种多股线束称为辫线。在工业应用方面，利用趋肤效应可以对金属进行表面淬火。

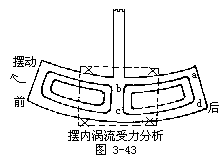
【电磁阻尼】当一块可在磁铁两极间摆动的铜板（付科摆），电磁铁未通电时，铜板要摆动多次才停止；电磁铁一旦通电，摆动的铜板很快停下。这种现象叫做“电磁阻尼”。电磁阻尼现象不难用楞次定律来解释。按照楞次定律的第二种表述：导体在磁场中运动时由于出现感应电流（在此就是涡流）而受到的安培力必然阻碍导体的运动。图3－43所示为一付科摆的磁场中摆头的示意图。近似地认为两极间的磁场集中在虚线所围的矩形内。“X”表示磁场方向垂直线面且背离读者。由于摆在前半部分磁通在减小，涡流的磁场应与磁铁磁场同向；摆的后半部分磁通在增大，涡流的磁场应与磁铁磁场反向。因此，涡流方向大致如图中箭头所示，以涡流线abcda为例分析受力情况。ab边和cd边受力不是向上就是向下，对摆动没有影响。ad边尚未进入磁场，故不受力。由左手定则可知bc边受力方向向右，即为阻力。电磁阻尼在实际中应用很广。使用电学测量仪表时，为了便于读数，希望指针能迅速稳定在应指的位置上而不左右摇摆。为此，一般电学测量仪表都装有阻尼器。它就是用电磁阻尼的原理来得到阻尼作用的。此外，磁电式电流计的线圈常绕在一个封闭铝框上，测量时，铝框随线圈在磁场中转动，铝框由于感应电流而受到安培力，同样起到电磁阻尼作用。除了仪表之外，电磁阻尼作用还常用于电气机车的电磁制动器中。

 

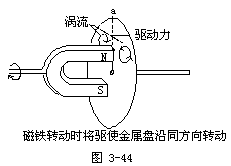
【电磁驱动】 在磁场运动时带动导体一起运动，这种作用称为“电磁驱动”作用。如图3－44所示，当磁铁转动时，设某时刻磁铁的N极处在金属圆盘的半径Oa处，根据楞次定律此时在圆盘上将产生如图所示的涡流，结果在该半径处形成由a流向O处的感应电流。该感应电流处于旋转磁场中，将受到磁场的作用力。此力将产生一个促使金属圆盘按磁场旋转方向发生转动的力矩。此时从磁铁S极处产生的感应电流所受的力而产生的力矩，同样是促使金属圆盘按磁场旋转的方向发生转动。结果金属圆盘按磁场的转动方向发生旋转。但是如果圆盘的转速达到了与磁场转速一样，则两者的相对速度为零，感应电流便不会产生，这时电磁驱动作用便消失。所以在电磁驱动作用下，金属圆盘的转速总要比磁铁或磁场的转速小，或者说两者的转速总是异步的。感应式异步电动机就是根据这个原理制成的。电磁驱动作用可用来制造测量转速的电表，这类转速表常称为磁性式转速表。我们知道在发电机中为了保证产生的交流电频率f=50秒-1，就必须控制转子的转速。在其他情况中，为了充分发挥机器的效率和正确地使用机器，也常需测量其转速，然后进一步加以控制和调节。用磁性式转速表测量转速时，将被测机器的转轴通过连接器和传动机构与转速表中的永久磁铁的转轴相连，永久磁铁一般是由一块充以四个极的磁钢制成，这便形成一个旋转磁场。在永久磁铁的上方有一个金属圆盘，称为感应片。感应片与永久磁铁间有很小的气隙，两者互不接触。当永久磁铁随着机器的转旋转时，感应片上将产生涡流，这涡流又将受到这旋转磁场的作用力，结果感应片被驱动，从而沿永久磁铁的旋转方向运动。感应片的转动将带动与感应片转轴相连的弹簧，将其扭紧，从而产生弹性恢复转矩。最后，当感应片转过一定的角度，由电磁驱动作用产生的转矩刚巧与弹性恢复的转矩抵消时，便达到一个暂时平衡状态。由机器带动转动的永久磁铁转速越快，感应片受到的电磁驱动作用所产生的转矩越大，因而指针的偏转角度就越大。这样，便可通过指针的偏转角度来显示机器的转速。

 

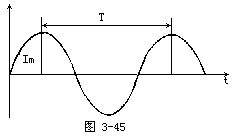
【在流电】简称“交流”。一般指大小和方向随时间作周期性变化的电压或电流。它的最基本的形式是正弦电流。我国交流电供电的标准频率规定为50赫兹。交流电随时间变化的形式可以是多种多样的。不同变化形式的交流电其应用范围和产生的效果也是不同的。以正弦交流电应用最为广泛，且其他非正弦交流电一般都可以经过数学处理后，化成为正弦交流电的迭加。正弦电流（又称简谐电流），是时间的简谐函数

i=Imsin（ωt+φ0）

图3－45表示上式的电流i随时间的变化规律，由此看出：正弦交流电需用频率、峰值和位相三个物理量来描述。交流电所要讨论的基本问题是电路中的电流、电压关系以及功率（或能量）的分配问题。由于交流电具有随时间变化的特点，因此产生了一系列区别于直流电路的特性。在交流电路中使用的元件不仅有电阻，而且有电容元件和电感元件，使用的元件多了，现象和规律就复杂了。

 

【交流电的频率和周期】频率是表示交流电随时间变化快慢的物理量。即交流电每秒钟变化的次数叫频率，用符号f表示。它的单位为周／秒，也称赫兹常用“Hz”表示，简称周或赫。例如市电是50周的交流电，其频率即为f=50周／秒。对较高的频率还可用千周（kC）和兆周（MC）作为频率的单位。

1千周（kC）=103周／秒

1兆周（MC）=10千周（kC）=106周／秒

例如，我国第一颗人造地球卫星发出的讯号频率是20.009兆周，亦即它发出的是每秒钟变化20.009×106次的交变讯号。交流电正弦电流的表示式中I = Imsin（ωt+φ0）中的ω称为角频率，它也是反映交流电随时间变化的快慢的物理量。角频率和频率的关系为

ω=2πf。

交流电随时间变化的快慢还可以用周期这个物理量来描述。交流电变化一次所需要的时间叫周期，用符号T表示。周期的单位是秒。显然，周期和频率互为例数，即

由此可见，交流电随时间变化越快，其频率f越高，周期 T越短；反之，频率f越低，周期T越长。

【交流电流的峰值】 简谐函数（又称简谐量）是时间的周期函数。其简谐电流

i=Imsin（εt＋α）

中的Im叫做电流的峰值，i为瞬时值。应该指出，峰值和位相是按上式中Im为正值的要求定义的。如对下面形式的函数

i=-5sin（ωt+α）

不应认为峰值为-5、初相为+α，而应把函数先写成

i=5sin（ωt+α+π）

从而看出其峰值为5，初位相为α＋π。

【交流电流的有效值】在交流电变化的一个周期内，交流电流在电阻R上产生的热量相当于多大数值的直流电流在该电阻上所产生的热量，此直流电流的数值就是该交流电流的有效值。例如在同样两个电阻内，分别通以交流电i（t）和直流电I，通电时间相同，如果它们产生的总热量相等，则说这两个电流是等效的。交流电的有效值通常用U或（I）来表示。U表示等效电压，I表示等效电流。设一电阻R，通以交流电i，在很短的一段时间dt内，流经电阻R的交流电可认为是恒定的，因此在这很短的时间内在R上产生的热量

dW=i2Rdt

在一个周期内交流电在电阻上产生的总热量

而直流电I在同一时间T内在该电阻上产生的热量

W=I2RT

根据有效值的定义有

所以有效值

根据上式，有时也把有效值称为“平均根值”。对正弦交流电，有i=Imsinωt，故

而其中

可见正弦交流电的有效值等于峰值的0.707倍。通常，交流电表都是按有效值来刻度的。一般不作特别说明时，交流电的大小均是指有效值。例如市电220伏特，就是指其有效值为220伏特，

【交流电的平均值】交流电在半周期内，通过电路中导体横截面的电量Q和其一直流电在同样时间内通过该电路中导体横截面的电量相等时，这个直流电的数值就称为该交流电在半周期内的平均值。

对正弦交流电流，即i=Imsinωt，则平均值与峰值的关系为

故，正弦交流电的平均值等于峰值的0.637倍。对正弦交流电来说在上半周期内，一定量的电量以某一方向流经导体的横截面，在下半周期内，同样的电量却以相反的方向流经导体的横截面。因而在一个周期内，流经导体横截面的总电量等于零，所以在一个周期内正弦交流电的电流平均值等于零。如果直接用磁电式电表来测量交流电流，将发现电表指针并不发生偏转。这是因为交流电流一会儿正，一会儿为负，磁电式电表的指针无法适应。如果附有整流器的磁电式电表（例如万用电表中的交流档）接入交流电路中如图3－46所示。那么在一周期内，只有正半周的电流通过电表，如图3－47中的实线所示，负半周期电流则过二极管D2而不通过表，图3－47中的虚线所示。在一周期内通过电表的电流平均值为

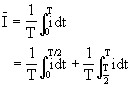
即半波整流后交流电的平均值和最大值的关系为

而交流电的有效值和最大值的关系为

所以

即正弦交流电经半波整流后的平均值只有有效值的0.45倍。

 

 

【位相】在交流电中i＝Imsin（ωt+α）中的（ωt+α）叫做位相（位相角）。它表征函数在变化过程中某一时刻达到的状态。例如，在

阶段，当ωt+α=0时达到取零值的阶段，等等。α是t=0时的位相，叫初相。在实际问题中，更重要的是两个交流电之间的位相差。图3－18画出了电压ul和u2的三种不同的位相差。图3－48a中可看到两个电压随时间而变化的步调是一致的，同时到达各自的峰值，又同时下降为零。故称这两个电压为同位相，也就是说它们之间的位相差为零。3－48b中两个电压随时间变化的步调是相反的，u1为正半周时，u2为负半周，u1达到正最大值时，u2达到负的最大值，则这两个电压的位相相反，或者说它们之间的位相差为π。图3－48c中两个电压的变化步调既不一致也不相反，而是有一个先后，它们之间的位相差介于0与π之间。从图3－48c中可以看出u1和u2之间的位相差是π／2。总之，两个交流电压或电流之间的位相差是它们之间变化步调的反映。

 

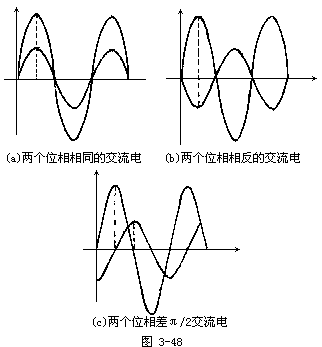
【交流电路中的电阻】纯电阻电路是最简单的一种交流电路。白炽灯、电炉、电烙铁等的电路都可以看成是纯电阻电路。虽然纯电阻的电压和电流都随时间而变，但对同一时刻，欧姆定律仍然成立，即

的波形如图3－49b所示。对纯电阻电路有：（1）通过电阻R的电流和电压的频率相同；（2）通过电阻R的电流峰值和电压峰值的关系是

的电流和电压同位相。图3－49a为纯电阻电路示意图。

 

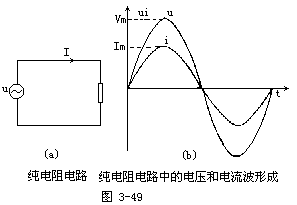
【交流电路中的电感】如图3－50所示，一个忽略了电阻的空心线圈和交流电流源组成的电路称为“纯电感电路”。在纯电感电路中，电感线圈两端的电压u和自感电动势eL间（当约定它们的正方向相同时）有

u=-eL

因自感电动势

故有

如果电路中的电流为正弦交流电流i=Imsinωt，则

其中Um=ImωL为电感两端电压的峰值。纯电感电路中的电压和电流波形如图3－51所示。由此可见，对于纯电感电路：（1）通过电感L的电流和电压的频率相同；（2）通过电感L的电流峰值和电压峰值的关系是

Um=ImωL

其有效值之间的关系为

U=IωL

由上式可知，纯电感电路的电压大小和电流大小之比为

ωL称为电感元件的阻抗，或称感抗，通常用符号XL表示，即

XL=ωL=2πfL。

式中，频率f的单位为赫兹，电感L的单位为亨利，感抗XL的单位为欧姆。这说明，同一电感元件（L一定），对于不同频率的交流电所呈现的感抗是不同的，这是电感元件和电阻元件不同的地方。电感元件的感抗随交流电的频率成正比地增大。电感元件对高频交流电的感抗大，限流作用大，而对直流电流，因其f=0，故XL=0，相当短路，所以电感元件在交流电路中的基本作用之一就是“阻交流通直流”或“阻高频通低频”。各种扼流圈就是这方面应用实例；（3）在纯电感电路中，电感两端的电压位相超前其电流位

的变化成正比，而不是和电流的大小成正比。对于正弦交流电，当电流i

当电流为零时，其变化率为最大，电压也最大。所以两者的相

 

 

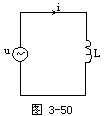
【交流电路中的电容】当把正弦电压u=Umsinωt加到电容器时，如图3－52所示，由于电压随时间变化，电容器极板上的电量也随着变化。这样在电容器电路中就有电荷移动。如果在dt时间内，电容器极板上的电荷变化dq，电路中就要有db的电荷移动，因此电路中的电流

对电容器来说，其极板上的电量和电压的关系是

q=CU

因此有

其中Im=UmωC为电路中电流的峰值。纯电容电路中的电压和电流波形如图3－53所示。由此可见，对于纯电容电路：（1）通过电容C的电流和电压的频率相同；（2）通过电容C的电流峰值和电压峰值的关系是

Im=UmωC

其有效值之间的关系为

I=UωC

由上式可知，纯电容电路中的电压大小与电流大小之比为

表示，即

式中频率f的单位为赫兹，电容C的单位是法拉，容抗Xc的单位为欧姆。可见，同一电容元件（C一定），对于不同频率的交流电所呈现的容抗是不同的。由于电容器的容抗与交流电的频率成反比，因此频率越高，容抗就越小，频率越低，容抗就越大。对直流电来讲f=0，容抗为无限大，故相当于断路。所以电容元件在交流电路中的基本作用之一就是“隔直流，通交流”或“阻低频，通高频”；（3）

率成正比，而不是和电压的大小成正比。对于正弦交流电，当电压为零

 

 

【交流电路中的欧姆定律】在交流电路中，电压、电流的峰值或有效值之间的关系和直流电路中的欧姆定律相似，其等式为U=IZ或

该式就是交流电路中的欧姆定律。应该注意的是（即与直流电路欧姆定律不同的地方）：由于电压和电流随元件不同而具有位相差，所以电流和电压的有效值之间一般不是简单的数量的比例关系。下面分两种基本电路来分析：（1）在串联电路中，如图3－54所示，R、L、C上的总电压不等于各段分电压的和，即

U≠UR＋UL+Uc。

 

压，决不是各个元件上电压的代数和而是矢量和。在电阻R上

在电感L上，ZL=ωL

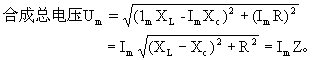
图3－55所示；（2）在并联电路中，如图3－56所示，在R、L、C上每个元件两端的瞬时电压都相等为U。每分路之间的电流和两端电压之间的关系为

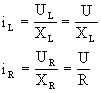
不同元件上电流的相位也各有差异。纯电感上电流相位落后于纯电阻电流

所以分电流的矢量和即总电流

 

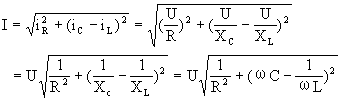
【交流电功率】 在交流电中电流、电压都随时间而变化，因此电流和电压的乘积所表示的功率也将随时间而变化。交流电功率可分为：瞬时功率、有功功率、视在功率（又叫做总功率）以及无功功率。（1）瞬时功率（Pt）。由瞬时电流和电压的乘积所表示的功率。Pt=i(t)·u(t)，它随时间而变。对任意电路， i与u之间存在着相位差i（t）=Imsinωt，u（t）=Umsin（ωt＋φ）。即

在纯电阻电路中，电流和电压之间无相位差，即φ=0，瞬时功率Pt=IU

位时间内所用的能量，或在一个周期内所用能量和时间的比。在纯电阻电路中，

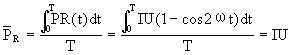
纯电阻电路中有功功率和直流电路中的功率计算方法表示完全一致，电压和电流都用有效值计算。

以上说明电感电路和电容电路中能量只能在电路中互换，即电容与电源、电感与电源之间交换能量，对外无能量交换，所以它们的有功功率为零。对一般电路的平均功率为

（3）视在功率（S）。在交流电路中，电流和电压有效值的乘积叫做视在功率，即S=IU。它可用来表示用电器本身所容许的最大功率（即容量）。（4）无功功率（Q）。在交流电路中，电流、电压的有效值与它们的相位差φ的正弦的乘积叫做无功功率，即Q = IUsinφ。它和电路中实际消耗的功率无关，而只表示电容元件、电感元件和电源之间能量交换的规模。有功功率，无功功率和视在功率之间的关系，可由图3－57所示的“功率三角形”来表示。

 

【功率因数】它是发电机输送给负载的有功功率和视在功率的比，即

可见功率因数cosφ是反应电能利用率大小的物理量。提高用电设备的功率因数就可以提高发电机总功率中的有功功率。

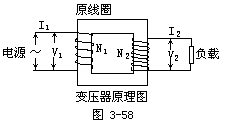
【变压器】 两个（或多个）有互感耦合的静止线圈的组合叫做变压器。变压器的通常用法是一个线圈接交变电源而另一线圈接负载，通过交变磁场把电源输出的能量传送到负载中。接电源的线圈叫做原线圈，接负载的线圈叫做副线圈。原、副线圈所在的电路分别叫做原电路（原边）及副电路（副边）。原、副线圈的电压（有效值）一般不等，变压器即由此得名。变压器可分为铁心变压器及空心变压器两大类。铁心变压器是将原、副线圈绕在一个铁心（软磁材料）上，利用铁心的高μ值加强互感耦合， 广泛用于电力输配、电工测量、电焊及电子电路中。空心变压器没有铁心，线圈之间通过空气耦合，可以避免铁心的非线性、磁滞及涡流的不利影响，广泛用于高频电子电路中。图3－58是变压器原理图。设变压器的原、副线圈中的电流所产生的磁感应线全部集中在铁心内（即忽略漏磁），因此铁心中各个横截面上的磁感应通量φ都一样大小。由于φ的变化，将使绕制在铁心上的每一匝线圈中都产生同样

 

则原线圈中总感应电动势

副线圈共有N2匝，总感应电动势

电源电压是按正弦函数规律变化的，因此铁心中的磁感应通量φ也将按正弦规律变化，设

其中φm为铁心中交变磁感应通量的峰值。因此

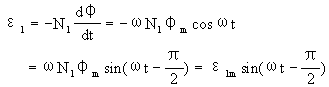
其中ε1m=ωN1φm，为ε1的峰值。其有效值为

同样

其中ε2m=εN2φm，为ε2的峰值。其有效值为

所以

即变压器的原、副线圈中感应电动势的有效值（或峰值）与匝数成正比。在实际的变压器中，原、副线圈都是用漆包线绕制的，其电阻r很小，故可略去由于线圈电阻而引起的电压降Ir。这样线圈两端的电压在数值上就等于线圈中的感应电动势。原线圈两端的电压即是变压器的输入电压U1，故

U1≈ε1

同样副线圈两端的电压就是加在负载上的变压器的输出电压U2，即

U2≈ε2

因此

上式说明：变压器的输入电压与输出电压之比，等于它的原、副线圈匝数之比。这是变压器的最重要的一个特性。当N2＞N1时U2＞U1，这时变压器起升压作用；当N2＜N1时，U2＜U1，这时变压器起降压作用。变压器在改变电压的同时，还起着改变电流的作用。在变压器空载时，副线圈中只有感应电动势，没有电流。但在原线圈中都有一定的电流I10、I10称为励磁电流，它的作用是在铁心中激发一定的交变磁感应通量φ，从而在原线圈中引起一定的感应电动势ε1，以平衡输入电压U1，即U1≈ε1得到满足。当副线圈与负载接通出现电流I2时，I2将在铁心中产生一附加的磁感应通量Φ2′。根据楞次定律，Φ2′将削弱铁心中原有的磁感应通量Φ的变化，从而使原线圈中的尖电动势ε1变小。但由于输入电压U1是不因变压器有无负载而改变，故变小的ε1便不再与U1平衡，结果将使原线圈中的电流比空载时大，设电流增大了I′，这一电流也在铁心中产生一附加磁感应通量Φ1′，以补偿Φ2′对原线圈电路的影响。当Φ1′和Φ2′两者的数值相等时，铁心中的磁感应通量又恢复到原来的值Φ，原线中的感应电动势也恢复到原来的值ε1，于是ε1又和U1相平衡，整个电路又恢复到平衡状态。因为Φ1′是由磁通势N1I1′，Φ2′是由磁通势N2I2引起的，故只有当

N1I1′=N2I2，

Φ1′和Φ2′才能相互抵消。这时原线圈中的总电流I1=I10＋I1′。当变压器接近满载（即负载电阻较小、变压器接近它的额定电流）时，I1>>I10，故I1≈I1′。于是

N1I1＝N2I2

即

上式说明：变压器接近满载时，原、副线圈中的电流与它们的匝数成反比。对于升压变压器来说N2＞N1，故I2＜I1，即电流变小；对于降压变压器，由于N2＜N1，故I2＞I1，即电流变大。通常所说“高压小电流，低压大电流”就是这个道理。这也符合能量守恒定律。其变压器的输入功率应等于输出功率。电压升高，电流必然以相应的比例减小。否则便破坏了能量定恒与转化定律。变压器的种类很多，常用的几种是：电力变压器，电源变压器，耦合变压器，调压变压器等。

【电力变压器】 这种变压器是用于输电网路。因为输电线上的功率损耗正比于电流的平方，所以远距离输电时，就要利用变压器升高电压以减小电流。这种高电压经高压输电线传送到城市、农村后，再用降压变压器逐级把电压降到380伏特和220伏特，供一般的用电户使用。电力变压器的容量通常较大。都是一些大型的变压器。

【电源变压器】 不同的电子仪器和设备以及同一仪器电路的不同部位往往需要各种不同的电压，如电子管的灯丝电压是6.3伏特，其板极电压需要300伏特；各种晶体管的集电极工作电压是几伏至几十伏；示波管的加速极电压达3000伏特等等。通常都用电源变压器将220伏特的市电电压变到各种需要电压。

【耦合变压器】 所谓耦合，在物理学上指两个或两个以上的体系或两种运动形式之间通过各种相互作用而彼此影响以至联合起来的现象，例如两个线圈之间的互感是通过磁场的耦合。无线电线路中常用作极间耦合的变压器，如收音机的中周、输入变压器、输出变压器都属于这一类，称为耦合变压器。耦合变压器的作用是多方面的，它还可以用来达到阻抗匹配等。

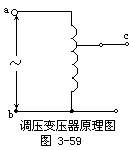
【调压变压器】 亦称为“自耦变压器”在生产和科学研究中，常需要在一定范围内连续调节交变电压，供这种用途的变压器叫做调压变压器。通常调压变压器就是一个带有铁心的线圈，线圈由漆包线绕成，以便滑动触点c能在各匝上移动，从而在c、b两端获得可调的交流电压。如图3－59所示。大容量的调压变压器也用于输电网路，以调节电网中的电压。

 

【互感器】 互感器也是一种变压器，一般它用于测量高电压和大电流。这是因为高电压和大电流均不能用交流伏特表和安培表直接去测量。而是借助于互感器把高电压变成低电压，或把大电流变成小电流，而把电压表或电流表接在副线圈一边（即低电压或小电流线圈的一边）测出低电压或小电流。根据伏特表或安培表测出的电压数值或电流的数值，再利用已知的变压比或电流比可计算出高压线路中的电压或电流。其接法如图3－60所示。从图中可以看出，在测量电压时是把原线圈并联在高电压电路中，副线圈上接入交流伏特表。且原线圈的线圈圈数多，副线圈的线圈圈数少。而测量电流时是把原线圈串联在被测电路中，副线圈接交流安培表，而原线圈的线圈圈数少，副线圈的线圈圈数多。这正是变压器的性质所决定的。

【隔直电容】 利用电容器的容抗与交流电的频率成反比的特性，在电路中用于隔离直流电，而只允许交流电通过的电容，在此电路中叫“隔直电容器”。例如，在放大器线路中的输入端和输出端，常设置这种电容，一方面隔断放大器的输入端与信号源之间，输出端与负载之间的直流通道，保证放大器的静态工作点不因输入、输出的连接而发生变化，另一方面又要保证需要放大的交流信号可以畅通地经过放大器放大，沟通信号源一放大器一负载三者之间的交流通道。隔直电容的名称是指电容器在电路中的作用而言。

 

【旁路电容】 可将混有高频电流和低频电流的交流电中的高频成分旁路掉的电容，称做“旁路电容”。例如当混有高频和低频的信号经过放大器被放大时，要求通过某一级时只允许低频信号输入到下一级，而不需要高频信号进入，则在该级的输出端加一个适当大小的接地电容，使较高频率的信号很容易通过此电容被旁路掉（这是因为电容对高频阻抗小），而低频信号由于电容对它的阻抗较大而被输送到下一级放大。旁路电容的大小一定要选择适当，若电容量大就有可能低频信号也被旁

量小，又不能充分的旁路高频。

【远程输电】 因为输电线上的功率损耗正比于电流的平方，所以在远距离输电时就要利用大型电力变压器升高电压以减小电流，方能有效地减少电能在输电线路上的损失。由发电厂发出的电功率是一定的，它决定于发电机组的发电能力。经过升压变压器可以把电压升高，但变压器却不能改变其功率，由

P=IU

得

由此看出，电压升高，电流减小。这一点也是和变压器的原理相一致的。对升压变压器来讲初级的电压低，电流大，而次级的电压高而电流小。

远程输电所需要的。因为在输电线路上的能量损失以其功率表示，即

P损=I2R

当电流减小n倍时，其功率损失将减小n2倍。故采取升压减流是减少电能损失的有效办法。设想我们用减小电阻R的方法来减少电能损失是不太有效的。因为远程输电路程较长，要减小电阻R，对同种材料来说就必须增加导线的横截面积。其截面增大n倍，也只能把电能损失减少n倍，这样导线就变得很粗，造成材料的浪费。显然，它远不如高压输送来得经济。当用高电压把电能输送到用电区后，需要逐次把电压降至380伏特和220伏特供给用户。这要靠降压变压器的功能。远程输电是变压器的一大功能。

【交流电的整流】 将交流电变成直流电的过程叫做“交流电整流”。整流可分为半波整流、全波整流、桥式整流等几种形式。通常的整流装置都是利用电子管和晶体二极管的单向导电的性能来整流的。例如，用锗、硅等半导体材料做成的整流器，已在许多方面得到广泛应用。为了适应较高电压的整流，可将许多单个整流器串联在一起封在一块绝缘材料中，称之为“硅堆”。整流器可将交流负半周的波形除去，使交流变成脉动直流。因此通过整流后的输出波形，只含有正弦波的正半周波形。一个理想的整流器可视为一个开关，正半周的交流输入时，就有电压输出，如同开关接通一样；反之，如果负半周交流输入，则无电压输出，也就相当于开关切断一样。所以当正半周的交流输入，此开关的有效电阻为零；而在负半周的交流输入时，有效电阻为无穷大。实际上的整流器，不可能这样理想，但相差不远。电子管整流器未导电时，其电阻极大，此时的电阻称为逆向电阻；整流器导电时，其电阻很小，此时的电阻为顺向（正向）电阻。无论任何情况，所有的整流器都只允许一个方向导电。此种特性称为单向传导或单向特性，二极管（包括晶体管）就具有此种单向特性。任何含有射极或阴极及集极或阳极的电子另件，都称为二极体（包括电子二极管和晶体二极管）。因为二极体中的电子只能向一个方向流。故所有二极体都有整流特性。

 

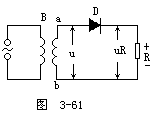
【半波整流】 整流时，通过整流器的只是交变电流的一个半周。半波整流是最简单的整流器，但效率很低，欲想将其整流出的电流波形变为平滑也比较困难。图3－61所示是一个简单的晶体管整流电路。半波整流器的输入波形和输出波形如图3－62所示。从图3－62中的半波整流器的输出波形，与输入交流波形的比较可知。当有电流流动的正半周时，输出波形的瞬时振幅，完全随输入交流波形的正半周的波形而变。所以在交流输入电压的正半周时，通过晶体管电流的波形，完全与交流输入电压的波形相同。由于只有输入交流电压的正半周输出，输入电压的一半就被损失了。因此半波整流的效率较低，半波整流器的另一缺点，就是输出的脉冲电压及电流的频率与交流输入电压的频率相同。要消除其脉动，必须要加滤波器，使整流器的输出成为平稳的直流。

 

【全波整流】 一种对交流整流的电路。在这种整流电路中，在半个周期内，电流流过一个整流器件（比如晶体二极管），而在另一外一个半周内，电流流经第二个整流器件，并且两个整流器件的连接能使流经它们的电流以同一方向流过负载。如图3－63所示即为一个全波整波的电路。图3－64为其整流前后的波形。与半波整流所不同的，是在全波整流中利用了交流的两个半波，这就提高了整流器的效率，并使已整电流易于平滑。因此在整流器中广泛地应用着全波整流。在应用全波整流器时其电源变压器必须有中心抽头。图3－63中的O点为中心抽头，于是a对O，与b对O的电压，具有180°相差，当变压器的输出电压处于正半周时（a正b负，O点的电势介于a、b之间，此时D1管因加的是正电压而导通，D2因加的是反向电压而截止，此时电流方向是由a线过D1、R到O，如图中实线箭头方向所示。当变压器输出的交变电压处于负半周时，则a端为负，b端为正，二极管D1截止而D2导通。这时电流方向是由b经D2、R到O，如图中虚线箭头所示。可见，无论正半周或负半周，通过负载电阻R的电流方向总是相同的。图3－64是全波整流的波形。全波整流使交流电的两半周期都得到了利用。其各项整流因数则与半波整流时不同。设变压器次极每边电压为Um则有

 

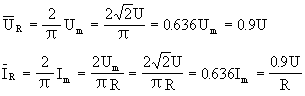
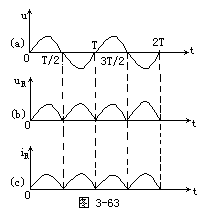
【桥式整流】 桥式整流为一全波整流，可变交流电压为较高直流电压，它不需要变压器有中心抽头。四个晶体二极管如图3－65所示的接法便构成一个桥式整流电路。四个整流器（晶体管）将输入交流电和负载连接在一起。当交流输入电压为正时，电流由输入的一边，经一个整流器、负载，再经另一个整流器，流至输入的另一边。当交流输入电压的负半周时，电流流经另一对整流器和负载。在这输入电压正和负的半周时，经过负载的电流方向相同。所以可在负载上产生脉冲直流电压。在实际的桥式整流电路中，四个整流器连接成一个整体，由外面联成桥式电路（即只要外面留出四个接线点，其中两头接电源，两头接负载）。桥式整流克服了半波整流和全部整流的利用率不高的缺点。在无线电技术和电气工程中广泛采用桥式整流电路。

 

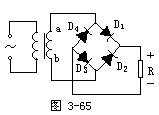
【滤波电路】 虽然整流器输出电压的极性永远一定，把交流电变为直流电，但此种电压是脉动的，并不能作为直流电压使用（如作电子管的直流电源），这是因为整流器本身输出的电压是脉冲或称涟波状。此种具有涟波状的整流器输出电压，在加于电子管的板极，往栅或控制栅电路前，必须先将涟波消除，使此电压平稳而几乎无脉动才行。为使整流器输出电压平稳，必先通过滤波器网路予以滤波，滤波电路是由电容器及扼流圈所构成，如图3－66所示。当电容器的外加电压增加时，电容器靠储存其内的静电场能量，以抵抗此增加的外加电压。但当外加电压降低时，电容器就将其蓄存的静电场的能量变为电压或流动的电流，作为外加电压降低时的补偿。整流器所输出的脉冲能量可蓄存于电容器的电场中，而在整流器所输出的两脉冲间，电容器缓慢的放电，因而经此电容器所输出的电压，其不稳定的涟波大为减小。这就是滤波电路要把一个电容器和整流器负载电阻并联的原因。当加于电感线圈（扼流圈）的电流增大，扼流圈靠存于其中磁场的能量以抵抗此电流的增加。但当流过扼流圈的电流减小时，扼流圈就将其磁场中所储存的能量变为电流，以继续维持电流的流动。因此将扼流圈与整流器的输出端及负载串联，可减小负载电流及电压的突然变化。与整流器输出端相串联的扼流圈，其作用也可由另一观点看：扼流圈对直流电而言，电阻（所谓的直流电阻）低，然而对交流电流（整流器输出电流带有变化的涟波电流）而言，阻抗（所谓的交流阻抗）非常高，因此直流较易于通过扼流圈，而在交流涟波通过时，涟波则被减小。

 

【滤波器】 滤波器是由电感器和电容器构成的网路，可使混合的交直流电流分开。电源整流器中，即借助此网路滤净脉动直流中的涟波，而获得比较纯净的直流输出。最基本的滤波器，是由一个电容器和一个电感器构成，称为L型滤波。所有各型的滤波器，都是集合L型单节滤波器而成。基本单节式滤波器由一个串联臂及一个并联臂所组成，串联臂为电感器，并联臂为电容器，如图3－67所示。在电源及声频电路中之滤波器，最通用者为L型及π型两种。就L型单节滤波器而言，其电感抗XL与电容抗Xc，对任一频率为一常数，其关系为

XL·Xc＝K2

故L型滤波器又称为K常数滤波器。倘若一滤波器的构成部分，较K常数型具有较尖锐的截止频率（即对频率范围选择性强），而同时对此截止频率以外的其他频率只有较小的衰减率者，称为m常数滤波器。所谓截止频率，亦即与滤波器有尖锐谐振的频率。通带与带阻滤波器都是m常数滤波器，m为截止频率与被衰减的其他频率之衰减比的函数。每一m常数滤波器的阻抗与K常数滤波器之间的关系，均由m常数决定，此常数介于0～1之间。当m接近零值时，截止频率的尖锐度增高，但对于截止频的倍频之衰减率将随着而减小。最合于实用的m值为0.6。至于那一频率需被截止，可调节共振臂以决定之。m常数滤波器对截止频率的衰减度，决定于共振臂的有效Q值之大小。若把K常数及m常数滤波器组成级联电路，可获得尖锐的滤波作用及良好的频率衰减。

 

 

【三相交流电】 一般家庭用电均为单相交流电，然而电流的大规模生产和分配以及大部分工业用电，则都是以三相交流电路的形式出现。高压输电线，通常是四根线（称为三相四线，其中有一条线为中线）。本质上还是三根导线载负着强度相等、频率相同、而相互间具有120℃相位差的交流电。所以代表这三根导线电压变化的曲线为相同频率的正弦波，位相互相错开三分之一个周期。对这三根导线分别对接地线的电压叫做“相电压”，图3－68中以实线R、S和T代表。三线中每两根线之间的电压叫做“线电压”，图3－68中虚线S－T、T－R和R－S所示。相电压和线电压对时间的变化以正弦曲线表示，峰值和有效值之间的关系完全与单相交流电之关系相同，即

图中零线以上至两条水平细线的高度表示相电压和线电压的有效值Uf和UL。它们之间的关系为

三相输电线的电压值常指线路电压的有效值。三相系统的主要优点在于三相电动机的构造简单而坚固。全世界均由这种电动机作为机械动力。

 

【三相发电机】 图3－69是三相交流发电机的结构示意图。这种发电机由定子和转子两部分组成。转子是一个电磁铁。定子里有三个结构完全相同的绕组，这三个绕组在定子上的位置彼此相隔120℃，三个绕组的始端分别用A、B、C来表示，末端分别用X、Y、Z来表示。当转子匀速转动时，在定子的三个绕组中就产生按正弦规律变化的感应电动势。因为转子产生的磁场是以一定的速度切割三个绕组，所以三个绕组中交变电动势的频率相同。由于三个绕组的结构和匝数相同，所以电动势的最大值相等。但由于三个绕组在空间相互位置相差120℃，它们的电动势的最大值不在同一时间出现，所以这三个绕组中的电动势彼此之间有120℃的位相差，其数学表示为

eA=Emsinωt

eB=Emsin(ωt-120°)

eC=Emsin(ωt-240°)

电动势变化的曲线如图3－70所示。发电机中的每个绕组称为一相。AX绕组为A相绕组，BY绕组称为B相绕组，CZ绕组称为C相绕组，在电气工程中，通常用黄、绿、红三种颜色分别标出。图3－69中的发电机定子有三个绕组，能产生三个对称的交变电动势，所以称为三相交流发电机。

 

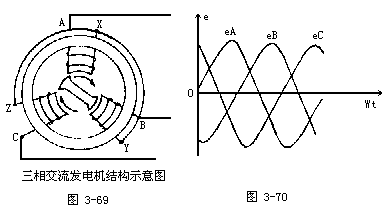
【单相交流电】 在电路中只具有单一的交流电压，在电路中产生的电流，电压都以一定的频率随时间变化。比如在单个线圈的发电机中（即只有一个线圈在磁场中转动）。在线圈中只产生一个交变电动势

e=Emsinωt

这样的交流电便是单相交流电。

【三相电源绕组的连接法】 对于三相交流发电机所发出的三相电必须采取适当的连接方法才能发挥三相交流电的功效。如果把三相发电机的每一相都用两根导线分别和负载相连，如图3－71所示，则每一相均不与另外两个相发生关系。这样使用的三相电路称为互不联系的三相电路，它总共需要六根导线来输送电能。这与单相制比较，既不节约导线，也没有任何优越之处，在实际应用中并不采取这种方法。常用的接法有：（1）星形接法；（2）三角形接法。

 

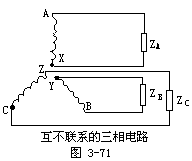
【电源绕组的星形接法】 把三相电源三个绕组的末端X、Y、Z连接在一起，成为一公共点O，从始端A、B、C引出三条端线，这种接法称为“星形接法”又称“Y形接法”。如图3－72所示。从每相绕组始端引出的导线叫做“相线”，又称“火线”。图3－72中的O称为“中性点”。从中性点引出的导线称为“中性线”，简称“中线”。这种具有中线的三相供电系统称为“三相四线制”。每相相线与中线间的电压称为“相电压”，其有效值分别用VAO、VBO、VCO）表示。每两根相线之间的电压称为“线电压，其有效值分别用VAB、VBC、VCA表示。相电压的正方向规定为自始端到中性点。线电压的正方向，例如VAB的正方向，规定为自始端A到始端B。如图3－73中的箭头所示。星形接法，相电压和线电压显然是不同的，且各相电压之间的相位不同，故在计算相电压和线电压之间的关系时应用矢量方法计算。例如，线电压VAB应该等于相电压 AO+ OB（由图3－73中可见）。但由于 OB=- BO，故 AB= AO- BO。同理有； BC= BO- CO、 CO- AO。图3－73表示相电压与线电压的矢量图，它表示了相电压和线电压之间方向和数量关系。由该图可以看出

VAB=2VAOcos30°

VBC=2VBOcos30°

VCA=2VCOcos30°

如果用VL表示线电压，用Vφ表示相电压，则线电压的大小与相电压的关系可写为

的相电压与线电压不等，因此采用三相四线制供电时，可以从三相电源获得两种电压。例如，我们所用的市电，其相电压为220伏特，线电压

图3－74表示了三相四线制的市电供电情况。

 

 

 

 

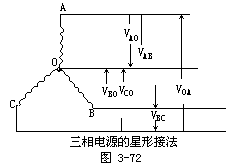
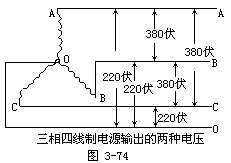
【电源绕组的三角形接法】 将一相绕组的末端与另一相绕组的始端相接，组成一封闭三角形，再由绕组间彼此连接的各点引出三根导线作为连接负载之用。这样的连接法称为“三角形接法”，也称“△接法”。如图3－75所示。由图中可见，在△接法中，端线之间的线电压也就是电源每相绕组的相电压，因此有

VAB=VAX

VBC=VBY

VCA=VCZ

即

VL=Vφ

 

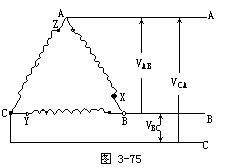
电源绕组的三角形接法和星形接法不同。在连接负载以前，三角形接法就已经构成了闭合回路。这一闭合回路的阻抗是很小的。所以三角形接法只有在作用于闭合回路的电动势之和为零时才可以。否则，在闭合回路中会有很大的电流产生，结果将使电源绕组过分发热而烧毁。三角形接法若接线正确，就能保证闭合回路中的电动势之和为零。从图3－76中可以看出，代表A相绕组和B相绕组的电动势之和的矢量 A+ B正巧与代表C相绕组的电动势矢量 C大小相等，但方向相反。所以这三个电动势之和应为零。但如果三相中有一相被接反，例如C相反了，则由图3－77可知，这时闭合回路内的总电动势不仅不等于零，而且等于C相电动势的两倍。所以三相电源作三角形接法时，绝不容许接错。星形接法比起三角形接法来具有如下的优点：星形接法时，发电机绕组的电压可以比三角形接法的低，结构上易于绝缘。例如同样输出380伏特的电压，星形接法时，绕组电压是220伏特，三角形接法的绕组电压则为380伏特。再有，采用星形接法时，可引出中性线，构成三相四线制供电系统，对用户可提供两种不同的电压，以适应不同的需要。但是三角形接法的绕组电流较小，因此绕组的导线可以细一些。这一点是星形接法所不及的。

 

【负载的星形接法】 三个负载的Za、Zb、Zc的一端连接在一起，成为负载中点O′，并接于三相电源的中线上，三个负载的另一端分别与三根端线（相线）A、B、C相接。如图3－78所示的接法就是负载的星形接法。在三相电路中，各相负载的电流称为“相电流”，如图3－78中的Ia、Ib、Ic。相电流正方向的规定与相电压的正方向一致。各端线中的电流称为“线电流”，如图中的IA、IB、IC。线电流的正方向规定为由电源到负载。负载作星形接法时，一条端线连接一个负载，从图3－78可以看出，线电流就是相电流，即

IA=Ia，IB=Ib，IC=Ic。

如果用IL表示线电流，Iφ表示相电流，即IL=Iφ，在三相四线制中，忽略输电线阻抗时，负载的线电压就是电源的线电压，并且负载中点O′的电位就是电源中点O的电位。所以每相负载的相电压就等于电源的相电压。由于电源的相电压和线电压是对称的，因此，负载的相电压和线

VL=Vφ

在负载是对称情况下Za=Zb=Zc。由于相电压是对称的，所以各相电流相等，而且是对称的，每一相的电流与对应的相电压之间的相位差都相同。可以证明，此时中性线中的电流为零。既然星形连接对称负载时，中性线上的电流为零，因此，有无中性线都对电路毫无影响，故可将中性线取去。这样就构成“三相三线制”。例如三相电动机就是三相对称负载，因此可用三相三线制星形接法。然而，在负载不对称的情况下，中性线上的电流I0将不等于零，在各相负载的差别不太大时，中性线中的电流比端线电流小得多，所以中性线可以用较细的导线。但此时中性线绝不能取消或让它断开，否则将使各相电压失去平衡，产生严重的后果。日常照明用的单相交流电源，就是三相供电系统中的一相。通常把三相电源的各相按星形连接，分配给用电量大体相等的三组用户。所以每家用户的两根导线中，一根是端线（火线），另一根是从中性线引出的。中性线通常接地，所以又称为地线。由于同一时刻各组用户的用电情况不可能完全一样，所以，一般说来三个相的负载是不对称的。如果一旦中性线断开，各相的电压就会偏离其正常值，以致有的用户的电压不足，有的用户的电压过高。由此可见，在负载不对称的情况下，星形接法的中线是不能断开的。保险丝和开关不允许装在中线上，中线需要用较坚韧的铜线做中性线，以免其自行断开而造成事故。

 

【负载的三角形接法】 图3－79所示为负载三角形接法的连接图。因为每相负载接于两根端线（相线）之间，所以负载的相电压就等于电源的线电压，即

 

VL=Vφ

通常电源的线电压是对称的，不会因负载是否对称而改变，所以三角形连接时，负载不论对称与否，其相电压总是对称的。然而，负载的相电流与线电流却不相等。各负载中相电流的正方向分别规定从A到B、从B到C、从C到A。线电流的正方向仍规定从电源到负载。如图3－79中箭头所示。各负载中相电流的计算方法与单相电路完全相同。如果负载是对称的，则各相电流大小相等，即

IAB=IBC=ICA

且各相电流与对应的相电压有相同的相位差φ，所以三个相电流也是对称的，如图3－80所示。在该图中还画出了代表线电流的矢量。对线电流 A来说，由图3－80可知，它应等于相电流 AB和 CA的差（因为 AB= A+ CA）。线电流 B和 C也如此。由图3－80可知线电流的大小与相电流大小的关系为

 

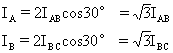
由此可见，对称负载作三角形接法时，线电流的大小等于相电流大小的

 

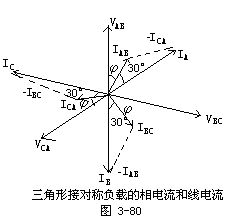
【三相电功率】 三相交流电的功率等于各相功率之和。在对称负载的情形下，各相的电压均为Uφ、相电流Iφ以及功率因数cosφ都相等。因此三相电路的平均功率可写为

P=3UφIφcosφ

种联接方式，平均功率都等于

但必须注意，计算三相电功率的公式，虽然对星形接法和三角形接法具有同一形式，却并不等于说同一负载在电源的线电压不变的情况下，由星形接法改为三角形接法时所消耗的功率也相等。

【感应电动机】 又称“异步电动机”，即转子置于旋转磁场中，在旋转磁场的作用下，获得一个转动力矩，因而转子转动。转子是可转动的导体，通常多呈鼠笼状。定子是电动机中不转动的部分，主要任务是产生一个旋转磁场。旋转磁场并不是用机械方法来实现。而是以交流电通于数对电磁铁中，使其磁极性质循环改变，故相当于一个旋转的磁场。这种电动机并不像直流电动机有电刷或集电环，依据所用交流电的种类有单相电动机和三相电动机，单相电动机用在如洗衣机，电风扇等；三相电动机则作为工厂的动力设备。

【电磁振荡】 由电路本身所具有的电场和磁场能量之间交互变化而产生的振荡，称为“电磁振荡”。电磁振荡的过程也是电路中的电流以及电容器极板上的电压，在最大值和最小值之间随时间作周期性往复变化的过程。能产生振荡电流的电路叫做“振荡电路”。最简单的振荡电路是由一个自感线圈和一个电容器串联而组成的回路，简称LC回路。如图3－81所示。即由电感L和电容C组成的振荡回路。振荡回路主要作用是使振荡器产生频率一定的正弦波。把图3－81a中的开关K倒向“1”，电池先向电容C充电，经过一段时间之后，把K从“1”移到倒向“2”，这时，回路中就发生了电磁变换现象，如图3－81b所示，其过程是先由充了电的电容C向电感L放电，在电容器向电感放电的时间内，原来充在电容器中的电能逐渐变成电感中的磁能。当电容器上的电荷放完时，C两端电压降至零，这时虽然C上不再放电了，但是我们知道通过电感线圈的电流是不能突变的，或者说，流过线圈的电流不可能一下子消失，因此电流仍按原方向继续流动。维持电流继续流动的是线圈中所贮存的磁场能量。当电流在回路中继续流动时，L就反过来向C充电，于是在电容器两端重新出现电荷，但电容器上的电压极性和原来相反，如图3－81c所示，在L向C反向充电的过程中，L中的电流逐渐减小，C上的电压逐渐增大，线圈的磁能又逐渐变成电容器的电能。当L中的电流减小到零时，线圈周围的磁场消失，磁能全部转变为电能，之后C又向L放电，如图3－81d。与前一过程比较，只是此时电容放电电流的方向相反了，其余过程与前一过程一样，回路中电流如此反复循环的现象，就是回路中产生了的电磁振荡。由此可见振荡实际上是回路中的电磁交替变换过程。通过这种过程，回路把原来的直流电能变换成交流电能，回路两端就有正弦交流电压产生，称为振荡电压，如图3-81所示。LC电路在振荡过程中，如果不再从外界获得能量，就会以一个固有的频率作振荡，该振荡频率称为振荡电路的固有频率；所对应的周期称为固有周期。电路的固有周期和固有频率，只和LC回路的电容和电感的大小有关，即

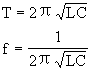
如果要改变振荡电路的周期和频率，可以通过改变电容和电感的方法来

因此前式可写成

这是一个二阶微分方程，它的解是

其中T、f、L、C的单位分别是秒、赫兹、亨利、法拉。

 

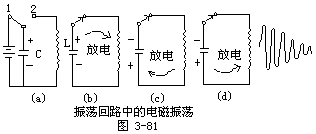
【电磁场】 任何随时间而变化的电场，都要在邻近空间激发磁场，因而变化的电场总是和磁场的存在相联系。当电荷发生加速运动时，在其周围除了磁场之外，还有随时间而变化的电场。一般说来，随时间变化的电场也是时间的函数，因而它所激发的磁场也随时间变化。故充满变化电场的空间，同时也充满变化的磁场。二者互为因果，形成电磁场。这说明，电场与磁场并不是两个可分离的实体，而是由它们形成了一个统一的物理实体。所以电与磁的交互作用不能说是分开的过程，仅能说是电磁交互作用的两种形态。在电场和磁场之间存在着最紧密的联系。不仅磁场的任何变化伴随着电场的出现，而且电场的任何变化也伴随着磁场的出现。所以在电磁场内，电场可以不因为电荷而存在，而由于磁场的变化而产生，磁场也可以不是由于电流的存在而存在，而是由于电场变化所产生。因此，交变电磁场可以存在于这样的空间范围内，该处

即没有电荷，也没有电流，而且也没有任何物体。电场与磁场之间的联系，不仅使电磁场在没有电荷和电流时能够存在，而且使这个场能够在空间传播。交变电场在相邻空间范围内激励起交变磁场，交变磁场又在毗邻的空间范围内激励起交变电场，交变的电磁场就是这样在空间传播。交变电磁场可以不通过导体而在空间传播，人们就利用这个特点进行无线电通信。由电流（即一连续运动电荷）产生磁场的事实说明，一个单独运动的电荷必定也能产生磁场。设想一

在与它相距为r的A点处的磁场为

B的大小为

 

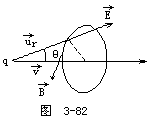
注意沿电荷运动方向磁场的大小为零，而在垂直于运动且通过电荷的平面上之磁场有一极大值。在A点由电荷q所产生的电场为

上式就是运动电荷产生的电场与磁场之间的关系式，令

式中c为光的速度或真空中电磁信号的速度。其值可以近似写成

c=3.0×108米/秒。

所以，虽然电荷在静止时只产生电场，但运动的电荷，可以同时产生电场和磁场。二者间的关系为

故电场及磁场不过是物质基本性质的两种形态。在沿载有电流的导线上，我们测得磁场B，但测不出电场E，这是因为在导体中除掉含有产生磁场的运动电荷外，尚有固定的金属正离子，这些正离子相对于观察者而言均为静止的，故它们并不建立磁场，但却产生电场，此电场与电子所建立的电场大小相等方向相反，所以净电场为零。然而，当离子沿一直线加速器的轴线运动时，我们得到一磁场及一电场。二者的关系为

【电磁波】 在高频电磁振荡的情况下，部分能量以辐射方式从空间传播出去所形成的电波与磁波的总称叫做“电磁波”。在低频的电振荡中，磁电之间的相互变化比较缓慢，其能量几乎全部反回原电路而没有能量辐射出去。然而，在高频率的电振荡中，磁电互变甚快，能量不可能全部反回原振荡电路，于是电能、磁能随着电场与磁场的周期变化以电磁波的形式向空间传播出去。电磁波为横波。电磁波的磁场、电场及其行进方向三者互相垂直。如图3－83所示。电磁波的传播有沿地面传播的地面波，还有从空中传播的空中波。波长越长的地面波，其衰减也越少。电磁波的波长越长也越容易绕过障碍物继续传播。中波或短波等空中波则是靠围绕地球的电离层与地面的反复反射而传播（电离层在离地面50～400公里之间）。振幅沿传播方向的垂直方向作周期性交变，其强度与距离的平方成反比，波本身带动能量，任何位置之能量功率与振幅的平方成正比。其速度等于光速（每秒3×1010厘米）。光波就是电磁波，无线电波也有和光波同样的特性，如当它通过不同介质时，也会发生折射、反射、绕射、散射及吸收等等。在空间传播的电磁波，距离最近的电场（磁场）强度方向相同和量值最大两点之间的距离，就是电磁波的波长。电磁波的频率γ即电振荡电流的频率，无线电广播中用

用的波长在10～3000米之间，分长波、中波、中短波、短波等几种。传真（电视）用的波长是3～6米；雷达用的波长更短，3米到几厘米。电磁波有红外线、可见光、紫外线、X射线、γ射线等。各种光线和射线，也都是波长不同的电磁波。其中以无线电的波长最长，宇宙射线的波长最短。

 

无线电波                                      3000米～0.3毫米。

红外线                                        0.3毫米～0.75微米。

可见光                                        0.7微米～0.4微米。

紫外线                                        0.4微米～10毫微米

X射线                                         10毫微米～0.1毫微米

γ射线                                        0.1毫微米～0.001毫微米

宇宙射线                                       小于0.001毫微米

麦克斯韦于1865年从理论上证明电磁波的传播速度应等于光速。因此他认为光波就是电磁波。1890年经赫兹于火花放电的实验中发现谐振现象后，证实电磁波的存在，并证实无线电波与光波，仅由之间的区别仅仅在于其频率的高低，无线电波频率较低。麦克斯韦关于光为的电磁波学说，只是从波动的角度描述了光的波动性，对于波长较长的电磁波，如微波和无线电波等，主要表现为波动性、但对于波长短的光波则在表现出其波动性的同时，也表现出粒子性。20世纪初爱因斯坦进一步提出了光的粒子性—一光子的概念，直到20世纪20年代在光的波动和粒子二重性的基础上，又发展出一门新的理论——量子力学。

【爱因斯坦】 Einstein，Albert（1879～1955年）物理学家。生于德国，1933年迁居美国。在物理学的许多部门中都有重要贡献。其中最重要的是在二十世纪初的一些新发现的推动下，建立了狭义相对论（1905年）；并在这基础上推广为广义相对论（1916年）。还提出了光的量子概念，并用量子理论解释了光电效应，他在阐明布朗运动、辐射过程、固体比热和发展量子统计等方面也有很多贡献。爱因斯坦曾访问过中国，正当他在上海时得知，由于他在理论物理和对量子理论方面的贡献而被授予1921年诺贝尔物理奖，但由于当时对相对论还有争议，而在授奖时并未提及他这一伟大贡献后期致力于相对论“统一场论”的建立，企图把电磁场和引力场统一起来，但无成效。爱因斯坦的理论，特别是相对论，揭示了空间-时间的辩证关系，加深了人们对物质和运动的认识，具有重要的历史意义。他的理论反映了自然科学唯物主义的倾向。

【赫兹】 Hertz，Heinrich Rudolph（1857～1894年）德国物理学家，生于汉堡。初习工程，后改物理学。入柏林大学随赫尔姆霍兹研习物理，后为其助手。麦克斯韦在1864年预言电磁波的存在。赫兹在1886年至1888年之间，用振荡的电火花产生高频电磁波，使这种电波在一定距离处不与它相联的导线回路中产生相同的电磁振荡，又证实光波与电磁波相同。因此发现电磁波，从而证实了麦克斯韦电磁理论，并开创了无线电、电视和雷达的发展途径。自1889年起赫兹在波昂大学任物理学教授，1894年元旦因患毒血证病逝波昂，年仅三十七岁。人们为纪念赫兹在电磁波方面的成就，用其名作为频率之单位。称之为赫兹常用英文字母Hz表示，简称为赫。

【赫兹振荡器】 赫兹振荡器如图3－84中左端所示，变压器T使金属板C与C′充电，这对金属板经由空隙P放电，空隙便成为偶极振荡器。电磁波沿PX方向传播，电场矢量将平行于Y轴，磁场矢量则平行Z轴。为了接收电磁波，赫兹利用一短导线，作成圆形，并留一小空隙；此项设计称为共振器。用在这类实验上的共振器直径必须比波长小，若放置一共振器，使其面与波的磁场垂直，变化的磁场在共振器中感应一电动势，结果在共振器空隙间产生火花。如果共振器之平面平行于磁场，则不能感应电动势，因此在空隙中无火花。欲产生电磁驻波，赫兹置一反射面（由良导体制成）于Q，在这样的情况下，当共振器位于磁场之节点上时，无论其方向如何，将表现有无感应电动势（或火花）。然而在磁场的反节点上，当共振器垂直磁场时火花最大。沿直线PQ移动共振器，赫兹发现节点与反节点之位置及磁场方向。借量度两相邻节点间距离，赫兹能计算波长λ，因已知振荡器之频率，利用方程式c=λγ，能计算出电磁波之速度。由此方法，赫兹为电磁波传播速度求得第一个实验值。

 

【赫兹实验】 赫兹在柏林大学随赫尔姆霍兹学物理时，受赫尔姆霍兹之鼓励研究麦克斯韦电磁理论，当时德国物理界深信韦伯的电力与磁力可瞬时传送的理论。因此赫兹就决定以实验来证实韦伯与麦克斯韦理论谁的正确。依照麦克斯韦理论，电扰动能辐射电磁波。赫兹根据电容器经由电火花隙会产生振荡原理，设计了一套电磁波发生器，见图3－85。赫兹将一感应线圈的两端接于产生器二铜棒上。当感应线圈的电流突然中断时，其感应高电压使电火花隙之间产生火花。瞬间后，电荷便经由电火花隙在锌板间振荡，频率高达数百万周。由麦克斯韦理论，此火花应产生电磁波，于是赫兹设计了一简单的检波器来探测此电磁波。他将一小段导线弯成圆形，线的两端点间留有小电火花隙。因电磁波应在此小线圈上产生感应电压，而使电火花隙产生火花。所以他坐在一暗室内，检波器距振荡器10米远，结果他发现检波器的电火花隙间确有小火花产生。赫兹在暗室远端的墙壁上覆有可反射电波的锌板，入射波与反射波重迭应产生驻波，他也以检波器在距振荡器不同距离处侦测加以证实。赫兹先求出振荡器的频率，又以检波器量得驻波的波长，二者乘积即电磁波的传播速度。正如麦克斯韦预测的一样，电磁波传播的速度等于光速。1888年，赫兹的实验成功了，而麦克斯韦理论也因此获得了无上的光彩。赫兹在实验时曾指出，电磁波可以被反射、折射和如同可见光、热波一样的被偏振。由他的振荡器所发出的电磁波是平面偏振波，其电场平行于振荡器的导线，而磁场垂直于电场，且两者均垂直传播方向。1889年在一次著名的演说中，赫兹明确的指出，光是一种电磁现象。第一次以电磁波传递讯息是1896年意大利的马可尼开始的。1901年，马可尼又成功的将讯号送到大西洋彼岸的美国。20世纪无线电通讯更有了异常惊人的发展。赫兹实验不仅证实麦克斯韦的电磁理论，更为无线电、电视和雷达的发展找到了途径。

 

【无线电波的传播】 由于频率不同，无线电波（电磁波）从发射天线向外发射的途径，最重要的有地波或地面波、地面反射波、直线波或视线波。地波只能传播较短的距离，而不能传送很远。如果需要接收地波，只能接收从近距离处发射来的无线电波。而发射角度较大的部分天波，都消失在较外层的天空；部分发射角度较小的电波，受带电荷的电离层的反射，返回到地面而被接收。

【无线电波】 无线电波（即赫兹波）。赫兹波除微波波段兼用厘米表示它的波长外，一般均用频率代替波长，其单位为赫（Hz）。频率范围约在30千赫（kHz）～30000兆赫（MHz）之间。其波长范围在10-3～104米之间。当赫兹发现电磁波以后，首先被用于无线电信之传递试验。最早的无线电讯，借控制火花放电时间，构成电码讯号。火花放电是一种波长很短的减幅波，它的振幅衰减极快，且干扰极大，故不能用它做长距离通信。后经改良用电弧放电以获得长波的等幅波，使通信距离稍增，但其副波干扰仍不能免，且能量较小不能作远距离通信。后来俄国人波波夫与意大利业余无线电家马可尼同时独立地发明天地线制，马可尼且于天线中加接调谐电路，试验越过大西洋电码通信获得成功，至此无线电通信开始进入实用阶段。由于弧光电波的影响，误认为波长越长，电力越大，通信距离越远；事实上在短波通信特性未发现以前，确实如此。欧洲各国甚至竟用波长10000米以上，耗费巨资建设电台，并用频率很低的交流发电机供应电磁波能直接发射。长波无线电之传递，以地波为主。其折射率在海面与平原之吸收率均较小。在传播途中的衰减大致与距离成正比，因受气候影响甚微，在有效距离内通信可靠，故迄今仍在使用中，不过波长已减至1000米左右。长波无线电特别适宜于极地通信及海上导航，因短波无线电在极地失去电离层反射作用，无法达成远距离通信。长波通信须高大之天线。自超短波及微波通信实现后，已可利用轻便之转继站构成通信网，故长波通信已在淘汰。中波波段为标准广播波段，其波长自200～545米。适用于国内及邻接地区间作广播之用。国土广大之国家均规定其最大电力及广播服务区。最大电力以天线发射之电场强度为标准。中波广播波段自540～1650千赫（kHz）。中波广播也可用于空中导航。短波通信之特点是：即使是不太强的无线电波也通跨越大洋，而完成极远距离通信。短波无线电讯，由于频率较高，其电磁波由天线发出后，因地球表面矿物质之吸收率甚高，故不论发射电力多大，不出百里以内，其沿地面进行的电磁波即被吸收以及，其衰减率以对数率随距离而加快。但在数百里以外的地区，因向空发射之天波受高空电离层的反射而再度出现。这种高空反射波的反射体是天空中大气因受紫外线辐射所形成的离子化气体层。围绕地球的这一层离子化气体称之为“电离层”。无线电波也和光波一样有四种特性：它能被物体吸收、反射、散射及折射。当电磁波前进时，遇金属物，则有一部分被吸收，有一部分即反射，且金属物与电子线波在不垂直又不平行之方向者，电磁波就发生散射。当电磁波经过不同的介质时，将发生折射的现象。

【无线电通信】 在电子学方向，无线电通信和无线电广播的地位是非常重要的。现代的无线电通信及广播系统，依照无线电报的电码，发射出周期性的断续无线电波（等幅波），此种系统称为无线电报。发出经语言或音乐的调变后的无线电波，这种系统称为无线电话。无线电系统所必须的最基本的元件有：（1）产生无线电频率段的电波（即射频电波）发射机。（2）控制射频电波的电键，使所发射出的电波随所需传递的信息变化。（3）发射天线将电波送至天空。（4）接收天线接收电波。（5）无线电接收机，用来选择及放大发射机所发来的信号，并将射频信号予以检波。（6）扬声器或耳机将已经检波的电波变为声波，如此可得到所得的信息。

【无线电发射机】 无线电发射机可产生一定频率的射频能量，然后天线以电磁波的形式发射出去。为使发射机所发射的电波能为人所用，需将信息附于此发射电波上。在无线电报方向，发射机送出等幅波，同时依照无线电码使等幅电波时断时续，如此将所欲传出的信息加在所发射出的射频电波上。无线电话发射机是借调频或调幅方式，将所欲送出的语言或音乐信号，加在发射机所发出的载波上。无线电发射机的种类很多，按信号的特性的不同，可分为无线电报发射机、无线电话发射机、无线电广播发射机、电视广播发射机等。

【无线电广播】 发出的无线电波能携带语言或音乐等声音讯号为广大听众服务，叫无线电广播。在无线电播音时。无线电广播电台，利用一种无阻滞的电波作为载波，并使播音管栅极电路中的线圈，与播音电路的线圈耦合。因此，语言音乐就被携带于载波上。利用所谓栅极转调的声波外差法，可将载波变成不等幅且随声波变化的电波。即好像在高频上驮着音频信号。收音机将此种电波接收并放大后，再加以检波。使之收到所需要的音频信号。然后输入到扩音器（或耳机）变成声音。

【电视】 电视是将分成无数因素的一系列静止图像，连续传送出。由于人类的视觉暂留功能，使连续出现的系列静止图像呈现景物移动的感觉。电视摄影机，在外观上和电影摄影机一样，可是内部却大不相同。电视摄影机里不是用电影底片而是录像带记录影像的动作。它主要是利用一种特殊的真空管（摄像管）。把被拍摄的像投影到管内的幕或像屏上。屏上覆有异常灵敏的感光层；它是由几十万个叫做“象素”的小点组成，就像眼睛中的视网膜是由无数个视神经细胞组成一样。为了把投影到感光屏上的影像变成电讯号并被传送出去，在摄像管内有一电子束从左到右、从上到下地扫过。这些象素，当电子束扫过某一点时，这点就能把它感受光的强弱，变成不同强弱的电讯号。在我国的电视系统中，最普通的电视画面是由600多行，每行又有800多个小点组成的。在播送电视时，每秒钟要播出25幅画面。可见图象所产生的电讯号的变化是极为迅速的。电讯号的强弱又对传送讯号的无线电波进行调制。调制好的无线电载波，就从电视发射天线发射出去。当你打开电视机，选送这些调好的电波时，就是利用这些电波来控制显像管里的电子束。显像管荧光屏内层的表面上，涂有一层荧光物质的膜。电子束扫过这层荧光膜时，电子束在每秒钟内多次自上而下地扫过荧光屏的每一部分。由电波携带的电视图象讯号控制着扫描电子束的强弱。强弱变化着的电子束打到荧光屏上，产生亮暗不同的光点，从而扫出各种图象。所以屏面上的画景，就和若干里外摄像机所拍摄的画景完全一致。电视的发声和收音机的原理是相同的。

【调制】 把一种波动变化特征加载到另一个波上，此种过程或所产生的结果称为调制。受调制的波称为载波，调制之波称为调制波。一般地说，就是高频振荡的某种性质随着某一低频信号的变化而变。这些变化的最简单情况，是高频振荡的幅度不为定值，而随作用于它的低频振荡而变化，这种情况叫做“调幅”，以区别于使频率发生变化的调制，即所谓“调频”或使相位发生变化的调制称之为“调相”。调制的用途，是借助于高频振荡以将某种信号发送出去。低频调制振荡相当于某种信号（如电报信号或某些声音），所以已调制的振荡便携带着这些信号传播出去。利用复原过程（检波），这些信号就可以从高频已调振荡中分离出来。调制由专门的调制装置或调制器来实现，在无线电广播中，一般是应用调幅制，但在我国的许多地区也建立了调频制的广播。电视广播则是利用调频。振荡的幅度变化越大，则调制度越大。调制度m通常用百分率

来度量，且式中的I1和I2分别表示振荡的最大幅度和最小幅度。

【调制器】 对振荡进行调制的设备。调制器的作用原理随着所用调制的型式而不同。如果是调幅，调制器应当随着调制电压的变化而改变高频振荡的幅度。为了这个目的，通常应用单独的电子管。电子管的工作，犹如一个高频振荡的放大器，不过它所给出的放大是随管子上所接调制电压的作用而变化。由于这样，经过电子管以后的振荡便是已经调幅的振荡。在三极电子管里，调制电压或是加到栅极（栅极调制），或是加到屏极（屏极调制）。在多极电子管里，调制电压常常是加在电子管的其他电极上。如果是调频，调制器应按调制电压的变化而改变高频振荡的频率。为了这个目的，通常都是应用所谓电抗管。该管是一个电抗，在调制电压的作用下，这个电抗的大小将发生变化。这个电子管接在被调振荡器的振荡回路中，当它本身的电抗发生变化时，就会使被调振荡器的振荡频率发生变化，同时也就使发射机所发射的振荡频率发生变化。有时也采用一些别的比较复杂的调制设备来进行调频。

【调幅】 调幅是借声频信号或视频信号的强度（大小）变化迫使射频载波的振幅随之变化。由单一声频电波所形成的振幅调制，如图3－86所示。假设图3－86a为1兆赫的载波，图3－86b为1千赫的单音。如果将载波及单音的声频电波同时加在一个电阻上，其合成的波形则如图3－86c所示，此时载波的振幅完全没有改变，只是其每周电波之瞬间极性有连续的改变而已，显然，这不是振幅调制，一无线电收音机无法判定这种信号的瞬时极性，所以也无法播出声音信号来。图3－86a是所要调幅的信号的载波，此种已调幅的载波是将载波与声频电波同时加在一电路上，但电路的电流与所加的电压不是正比关系，也就是此电路是非线性的，不能用欧姆定律来解释。为了达到调幅的目的必须利用非直线型电路。当电子管作用于特性电线的非直线部分时，电子管可说是一个理想的调制器。功率放大器的失真，是由非直线的电子管特性曲线所引起的。在某种意义上看，也可将振幅调制当作振幅失真来看，所以造成失真或调制，必须要一个非直线型电路。当电子管作用于特性曲线的非直线部分时，电子管可说是一个理想的调幅器。图3－86d是仅由两个额外频率的电波所形成的调幅载波，一个是1001千赫，也就是等于载波频率1000千赫与声频电波频率1千赫的和；另一个是999千赫，也就是载波频率1000千赫与声频电波频率1千赫的差，1001千赫的频率，称为高旁频率，999千赫的频率被称为低旁频率。在无线电波广播方面，调制载波的声频电波频率范围可达10 000赫（10千赫），每一声频电波频率都能产生一个高旁频率及一个低旁频率，因此各声频频率所产生的总高旁频率与总低旁频率，就形成两个频带，一为高旁频带的最高频达1010千赫（对10千赫声频电波而言，低旁频带的最低频率达990千赫。因此借1000千赫载波以传送声频频率达10千赫范围内的电波时，发射频道这频带宽度必须有20千赫（从990～1010千赫），这不只对声频电波而言，就是对视频电波的传送，也是如此，就一般频道的总频带宽度言，也都是所需传送信息电波频率宽度的二倍。由此可知发射机及接收机的调谐放大器，不只通过射频载波一个频率，必须能通过整个频带宽度方可。为了能从已调幅的载波获得信息，所有的发射机及接收机电路，必须能通过具有高旁频带及低旁频带的全部频带。调谐电路必须具有选择能力，使所需的频带通过，并排斥不需要的频带。只讨论一些对载波振幅变化的原理还是不够。调制的程度是一个非常重要的因素，因为正是调制程度决定被传送的信号的强度及特性。图3－87是各种不同程度的调幅载波。图3－87a是声频调制信号电波。图b是未被调幅的载波。调制深度很低的已调载波则示于图3－87c，已调载波的振幅大小变化，完全随声频调制信号的变化而改变。但其振幅变化的程度较小。接收机的检波器之输出，只对载波的振幅变化有相应变化，而对载波的绝对大小无关。已调制载波的调幅程度很小时，声频信号将不会太大，并且此信号可能会被较强的杂波所湮没。如果调制深度大，声频信号一定非常强而又清晰。图3－87d的射频载波，已经被调制到最大的可能程度，振幅的最大值，是原来未经调制前载波振幅值的二倍，称为百分之百的调幅。如果调幅信号（即声频信号）电波的振幅再增大的话，所接收的信号电波，将产生失真的现象。

 

 

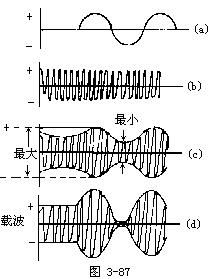
【调频】 频率调制是借改变载波的频率变化而成，载波的振幅保持恒定，因此在接收后，已调载波振幅的变化，根本不必再出现于声频电波中，所以电杂波引起的振幅变化，完全没有作用。这也表示不受杂波影响的频率调制信号杂波比值，比振幅调变小得多，因此频率调制发射机的功率虽低，也可以得到相同音质的接收。再者，因为频率调制载波的频道，包括所传送20～15 000赫的整个声频频带，所以频率调变具有高度传真性。频率调制所需频道的频带宽，比振幅射频调制大。在发展频率调制的同时，很宽的特高频率的频带从（30～300兆赫）内的信息传送，已经可得到了。频率调制广播所规定的总频带为88～108兆赫（即总频带宽为20 000千赫），每一广播电台所允许频道的频带宽为200千赫；这表示在同一地区，可以同时有100家电台存在。调频也有它的缺点，如要达到调频的作用，发射机的载波频率必须要在一较宽的频率波段内偏移。虽然优良调频广播，并不需要发射机的频率偏移达最高允许限度（指定中心频率上下各75 000赫），但高传真度性能的调频广播电台差不多都能接近这个限度。这样宽的频率范围在通用无线电广播波段是无法容纳的，故通用调频发送指定于88～108兆赫之间。在这频率波段中，调频遭遇到和电视观众所习知的同样缺陷，这便是调频的接收主要只限于离发射天线视线距离内，边远区的接收效果，在每天内的变化极大。调频的另一缺点是每一发射机需要一较宽的频率波段，在波段重叠的情形下便只能收到最强的发射机。这样便需要把全国各地发射机的工作频率，仔细地加以分配，以避免任何可能的重叠。

【谐振电路】 由于天线线圈中有各种广播电台的射频波通过，所以必须选择所希望要的频率，这种功能叫谐振，具有这种作用的电路叫谐振电路。这种电路是由线圈与电容器构成。当有高频电流经过天线时，因电磁感应而在谐振线圈中也有高频电流通过。这时，在天线与地线电路中，虽有各种频流振荡电流通过，可是，在谐振电路中，由于线圈与电容器的作用，只有某一种固定频率的振荡电流通过特别多，这种现象叫电振荡。某一特定线圈和特定电容器仅能谐振一个频率，改变调谐电路中的电感和电容值均可改变谐振频率。了解此特性，就容易明白谐振电路如何选择电台。事实上没有一个调谐系统是完美的，和谐振频率很接近的信号也将进入收音机，到达扬声器。不过收音机调谐的频率信号，其声音略比其他频率为强。在射频放大器的选择性，是由它的调谐电路决定的，调谐电路中线圈的电阻越是比它的电抗低，则选择性越高，线圈的选择性通常以Q来表示称之为品质因数，它等于线圈的电抗除以电阻。谐振回路一般作为收音机的输入回路。

【检波】 将接收电路中之高频交变电流整流，便成为单向之脉动直流，以引起膜片振动。这种把无线电波讯号变成声音信号的手段，称为检波。凡具备单向传导或一方向导电优于另一方向的工具，都可以提任检波工作。解调制或检波的程序正与调制的程序相反，检波就是将在已调制载波所含的信号分出。关于对已调频载波的检波比较复杂，通常先使已调频载波成为等幅已调频载波，以减低杂波，后将已调载波的频率变化，转变成声频信号波幅变化。通常接收电波听筒膜片具有惯性，不能随振动电流之频率而振动（即使随之振动也超出听力范围而无法觉察）；故需另置检波器于谐振电路中，以使调幅波变为单向脉动电流通入收话器中，再由此变为声波传入人耳。最常用的检波器有晶体检波器，二级管检波器和真空管检波器等等。

 

【传真】 利用电线或通过无线电发送不动图象（信件、图片、照片、报纸等）。传真的原理与电视相似，不过因为不动图像的发送可以延续足够长的时间，所以图像的分解速度及信号的发送速度都不要求很快。这种对图象的复合与分解，都可以采用机械装置；对于发送，可以采用相当窄的频带，也就是可以利用普通的通信线路，例如利用电话线路就可以传真。宇航中拍摄的照相，都是采用电视的传真照相，这些照片是利用电波传送回来的“传真照片”。传真的照片是把传送的照片改为电讯信号播放，由受信的接收站收取这些“电讯信号”，再改成照片，同时也可收取世界各地的传真广播，遇有重大新闻时，可以收取照片，再行转印成的新闻照片分发，这种照片的价值及其功用是很高的。它的传送方法如图3－88所示。发放照片传真的地方，是先把照片卷在一个圆形筒上，这个圆筒以一定的速度旋转，在旋转的画面上，依靠一个很细小的光点，以扫描的方式扫过整个画面。照片的影像可以看做是由无数个深浅不同的小点组成，所以当扫描的光点扫到照射照片上的某个小点时，小点较浅的地方反射强，而在较暗地方反射弱。其光线反射的亮度不同，便由光电管（把光线变成电信号的电子管）反射光的强弱转变为电流的变化。于是，照片的图象被转变为电讯号。电讯信号再通过发信机将电波传播到很远的地方。受信一方的设备，恰好和发信地相反，把电流的变化改做强弱的光线，就可以在感光胶片上得到画片的底片，所以，受信的一方也要有如发信地方的那样圆筒，用同样速度旋转；在圆筒上套上感光片，为防止其他光线的干扰，圆筒必须装在暗箱里。受信的接收机收到发来的电信时，把强弱不同的电信号变为扫描光点的强弱变化，光点扫到感光的不同部位，产生不同的曝光效果，从而得到从远方传送来的传真照片。

【雷达】 雷达是利用无线电技术进行侦察和测距的设备。它可以发现目标，并可决定其存在的距离及方向。雷达将无线电波送出，然后经远距离目标物的反射，而将此能量送回雷达的记发机。记发机与目标物间的距离，可由无线电波传雷达的目标物，再由目标物回到雷达所需的时间计算出。雷达的基本原理与无线电通讯系统的原理同时被人所发现，赫兹与马可尼两人都曾用超短波试验其反射情形，这也就是所谓雷达回波。赫兹用金属平面及曲面证明，电波的反射完全合乎光的反射定律。同时赫兹度量脉冲的波长及频率，并已计算其速度也发现与光相同，这也就是所谓的电磁辐射。雷达送出短暂的电波讯号的程序，称为脉冲程序。雷达的基本作用原理有些相似于声波的回声。唯一与声波测量距离的不同点，在于雷达系统具有一指示器，指示器中包含有一个与电视收像管相同的观察管。此管可将雷达所发出的脉冲及回波，同时显示于其标有距离的基线上。还有其他指示器，使雷达借天线所搜索的资料，制成一个图，从图上立即可以定出目标物的区域距离及方向。因为雷达的作用完全是借电波的反射原理而成，所以必须用频率在1000兆赫到10 000兆赫的类光微波方行。雷达所发射的电波可借抛物面形的反射器，使其成为极度聚焦的波束，这就像探照灯所射出的光束一样。此波束借旋转天线及抛物体形反射器的精密控制，有系统地对空间进行搜索。当波束从目标物反回来时，天线所指的方向，就表示目标物对天线的水平方位角。以角度为单位所表示的水平方位角，通常都显示于指示器上。为了决定目标物与雷达间的距离，雷达的发射脉冲距接收到回小的时间，必须精确测定。因为雷达电波在空中以每秒约30万公里的光速进行，因此在每微秒的时间内，电波行进约为300米。由于雷达脉冲必须从雷达行至目标物，再由目标物回到雷达，但目标物距雷达的距离，为雷达脉冲总行程的一半。约为每微秒150米。此时间可利用电子束在阴极射线管的屏幕上，以直线扫描指示出。借电子束，以已知变动率（如以每微秒0.01米）作水平偏向，因此电子束打在萤光屏上所留的痕迹，就形成一个时间标度，或直接用尺，来表示。如雷达天线送出一个1微秒长的脉冲，同时指示器的阴极射线管电子束在屏幕上，以每100微秒0.0254米的变动率开始扫描。再假设雷达脉冲在30000米的距离从一飞机反射回到线。当1微秒长的脉冲离开天线的同时，在雷达指示器的左侧也显示出一个0.025厘米长的主脉冲（发射脉冲）。由天线发射的脉冲，到飞机进行了30000米的距离，需时100微秒，然后反回天线也需100微秒。结果微弱的脉冲回波也显示于指示器上，其与主脉冲之间有5厘米的距离，或指示为200微秒。由于脉冲本身有1微秒的长度，所以量度距离时，必须量度两脉冲的前缘间距离。由于回波信号太弱，所以一个单一回波信号显示于指示器，很难被发现。因此回波信号，必须于每秒内，在指示器上重复显示数次，显示的方法是借电子束随天线扫描的速率（通常天线以每分钟15到20转转动）在指示器上扫描而得。雷达无论在平时及战时，都已被广泛的应用。在二次世界大战时使用雷达的目的，只是为了预知敌机的接近。用于预警网的预警雷达，预警雷达天线都是极大的转动抛物面形反射天线，或静止双极矩阵天线。战时雷达的应用很快就被扩展到地面拦截控制，以及高射炮和探照灯的方向控制等。这些所谓的射击控制雷达不仅能察知敌机的所在，并能自动决定高射炮的发射方向及使其发射。由于雷达可度量其与目标物间的距离，当然也可以从飞机上测量距地面的垂直高度。常用的各种脉冲式雷达就可度量一架飞机的高度，供飞行员飞行的参考。然而对很低的高度（低于1000米），因距离太近，脉冲式雷达的回波有与其发射出的主脉冲合并的趋势。因此大多数雷达测高仪都不用脉冲输出，而用等幅调频电波。雷达测高仪的发射天线，送出一垂直无线电波束，此电波的频率连续不断的变化。当信号离开发射天线的瞬间，其信号的频率为某一频率。然后当信号由地反射回到测高仪的接收天线后，因接收机内有一相位鉴别器（或简称为鉴相器），鉴相器可将接收到的回波，与正在发射出的信号频率（或相角）作一比较。因为当回波回到接收天线，已经过了一段时间，当然此时发射天线所发信号的频率，也已改变。利用已知每秒周数的频率偏差，就可决定出电波由发射天线到地，在回到接收天线的时间，因此可计算出飞机距地的高度。关于电波往来所需的时间与相应的高度，事先已经算出，并直接标示在指示器上，所以可以直接从指示器上读出飞机的高度数值。除此之外，雷达还可以用在飞机和船舶的导航，作为某一城市、机场，高山或某一特定点的辨别符号用的雷达指标，都已事先标示于航行图上。

【通讯卫星】 火箭、飞弹、太空航具，或其他人造物体被置入绕地球公转之轨道上者，均称为人造卫星。而作为通讯用的卫星则称为“通讯卫星”。通讯卫星有两种，被动的和自动的。被动的通讯卫星仅仅是一具反射器。播送站向那卫星发射讯号，这讯号被传送到地面上另一个遥远的接收站。自动的通讯卫星接收讯号后，把它加强，再把它发送出去。它们包含有接收、加强和播送的设备，以特殊的电池或太阳能电池作动力。为了把通讯微波信号，传送得更远，经常采用同步通讯卫星。所谓同步卫星，是指卫星经发射后，它与地球某点的相关位置不变，实际上这些卫星并非在那里静止不动，因为要达到同步的目的，卫星必然要以和地球自转的角速度相同的速度围绕地球转动。根据开普勒第三定律，卫星绕地球的周期因其平均轨道高度增加而增长。故在某一定高度时可期望致使卫星的周期与地球自转周期相同，如此则卫星与地球某点之相关位置可以不变，这个高度大约是35783公里。此种高度的卫星称为同步卫星。严格说来，仅是高度这一要求还不够，而必须又是在赤道面中圆形轨道上的卫星才真正能与地球某点相关位置不变。需要正圆形轨道是根据开普勒第二定律而来，此定律说明卫星在椭圆轨道上时其速度永远在改变，在最低点时为最高速，最高点时为最低速，故在椭圆轨道上的同步卫星，因为速率不定的结果，对地球上某点时而偏东时而偏西。卫星在赤道面轨道运行时称之为赤道轨道，如果轨道平面与赤道面成一个角度时，这个同步卫星称之为倾斜同步卫星，这时卫星对地球上某一点来说会时而偏北时而偏南。以这样的同步卫星作为通讯用的卫星就称之为“同步通讯卫星”由于这种卫星和地球上的某一地区处于同步，如果在赤道上空36000公里以外的高处，设置三颗同步卫星，就可以把微波信号传到全世界的任何地区。

【电子计算机】 电子计算机包括模拟计算机和数字计算机两大类，都具有度量和计算的简单观念。然而通常所指的计算机，都指数字计算机而言。实际上，每架大型的数字计算机，包括有成千个恒温器，求积计和小型模拟计算机，这些仪器都是以度量他量，来计算某量的。电子计算机的构造极为复杂，通常可分为输入、输出、记忆、计算及控制五大部分。又记忆、计算及控制三大部分称之为“中央处理机”。图3－89为其方框图。电子计算机的计算，是有一定的法则。通常它在作计算或逻辑运算时，已有一部分的法则储存于电子计算机中，其余的法则如数目字或指令，则由外界输入。因此，电子计算机在作运算时，必须将许多输入资料事先存储于记忆单位，然后再根据需要，依次自储存单位取出，进行计算。如图3－89记忆单位与计算单位是相互沟通的，记忆单位所存储的资料，送入计算单位中，经过运算后的结果，再送回记忆单位储存。此外，指令执行的先后次序，必须根据需要而且有一定的规则，因此电子计算机除了以上两单位外，必须有一控制单位，来执行所需要的指令。经由计算的结果，并不能永远储存于记忆单位，必须取出，而用数目字或字母表达于报表或卡片上。电子计算机的功能，除了可以预测变幻无常的气象、进行医疗诊断，帮助引导人们到月球去，加强各大城市之间的通讯等。电子计算机还有绘制建筑图样和商业图表的能力，并被用来绘制各种美术图案。现在电子计算机已成为现代化办公室不可缺少的手段，在发达的国家电子计算机已是入家庭和生活中。

 

【电子显微镜】 是一种电子仪器设备，可用来详细研究电子发射体表面电子的放射情形。其放大倍数和分辨率都比光学显微镜高得多。因为普通光学显微镜的放大倍数和分辨率有限，无法观测到微小物体。以电子束来代替可见光束，观察物体时，分辨率就没有波长要在可见光谱之内的限制，不过电子透镜无法作得像光学透镜那样完美。因此理论上，电子显微镜所具有的分辨率并不可靠。目前电子显微镜的分辨率可达10-7厘米（约为原子直径的两倍）。通常电子显微镜的放大率是200～200 000倍，再经照相放大可达1000 000倍。电子显微镜有两大类：（1）发射型。（2）电磁、静电扫描型。前者用于研究电子放射现象；后者用以增加普通光学显微镜的应用范围。1924年法国物理学家德布洛意指出电子和其他的粒子也都具有和光类似的波动性质。他还求出了计算它们波长的公式。

式中m是粒子的质量而v是它的速度，h是普朗克常数。此公式发明的年代较早，后来由美国科学家德维生及革末用实验证明其正确性。既然正确，也就告诉人们：虽然电子是一种可称重量，可数数目，可以被电子枪发射的粒子，但它同时又是一种波。从公式中我们可以看到，如果使电子运动的速度十分巨大的话，它就可以明显地显示出波长极短的波动性。如果在光学显微镜中被观察物的大小比光波波长还小的话，人们就不能分辨出来。在实用上通常取波长λ的三分之一作为限度，光波波长约在6×10-5厘米左右，它的三分之一就是2×10-5厘米了。然而，有很多科学家急待观察的微小东西如病毒体、胶体粒子及结晶结构的大小都在这限度以下，既然如此，如果我们把一颗运动中的电子加速，使它产生巨大的速度，从而有极短的波长，则利用此原理制成的电子显微镜就能观察到极微小的物体了。把电子加速的办法是在真空中加上若干万伏的高电压，电子就会以极快的速度射出，其波长可能会达到4×10-10厘米这样短的长度，也就是说：电子显微镜

是理论上的结果，在实际上由于仪器等等原因，不可能达到这样理想的地步。但无论如何，电子显微镜已可以放大五万倍以上；而有些精良到可将物体放大十万倍。电子显微镜中有一个电子枪，电子在枪集束射出，正像光学显微镜中利用光学透镜的成像作用得到显微的放大像一样，在电子显微镜中用磁透镜，使电子束会聚成像。我们把一片待观察的物体，例如一片很薄的晶体，放在电子显微镜中，电子束会就射向这片物体上，在一块荧光幕上就会得到一个放大的影像。如果在电子显微镜中用感光的底片代替荧幕的话就可以得到一张微观世界的珍贵图片。而一些特别好的电子显微镜，甚至可以观察到一些巨分子的结构！这些图片在科学研究上的价值十分重大。当然，在电子显微镜中不会这样简单，它要涉及电子射线通过物体产生不同的散射而造成明暗不同的影响。最近，有些电子显微镜是利用电子束的反射来观察较厚的物体例如病菌、病毒及其他极微小物体的巨分子组织。而最新的显微镜用的却不是电子显微镜，而是离子显微镜借以达到更短的波长，米勒曾经利用氦的离子显微镜成功地拍摄到金属表面的单独分子运动！这种离子显微镜可以分辨原子之间相隔百万分之二十七厘米的空隙，它是目前显微镜中最好的一种。