一、力 学
【力学】物理学的一个分支学科。它是研究物体的机械运动和平衡规律及其应用的。力学可分为静力学、运动学和动力学三部分。静力学是以讨论物体在外力作用下保持平衡状态的条件为主。运动学是撇开物体间的相互作用来研究物体机械运动的描述方法,而不涉及引起运动的原因。动力学是讨论质点系统所受的力和在力作用下发生的运动两者之间的关系。力学也可按所研究物体的性质分为质点力学、刚体力学和连续介质力学。连续介质通常分为固体和流体,固体包括弹性体和塑性体,而流体则包括液体和气体。
16世纪到17世纪间,力学开始发展为一门独立的、系统的学科。伽利略通过对抛体和落体的研究,提出惯性定律并用以解释地面上的物体和天体的运动。17世纪末牛顿提出力学运动的三条基本定律,使经典力学形成系统的理论。根据牛顿三定律和万有引力定律成功地解释了地球上的落体运动规律和行星的运动轨道。此后两个世纪中在很多科学家的研究与推广下,终于成为一门具有完善理论的经典力学。1905年,爱因斯坦提出狭义相对论,对于高速运动物体,必须用相对力学来代替经典力学,因为经典力学不过是物体速度远小于光速的近似理论。20世纪20年代量子力学得到发展,它根据实物粒子和光子具有粒子和波动的双重性解释了经典力学不能解释的微观现象,并且在微观领域给经典力学限定了适用范围。
【经典力学】经典力学的基本定律是牛顿运动定律或与牛顿定律有关且等价的其他力学原理,它是20世纪以前的力学,有两个基本假定:其一是假定时间和空间是绝对的,长度和时间间隔的测量与观测者的运动无关,物质间相互作用的传递是瞬时到达的;其二是一切可观测的物理量在原则上可以无限精确地加以测定。20世纪以来,由于物理学的发展,经典力学的局限性暴露出来。如第一个假定,实际上只适用于与光速相比低速运动的情况。在高速运动情况下,时间和长度不能再认为与观测者的运动无关。第二个假定只适用于宏观物体。在微观系统中,所有物理量在原则上不可能同时被精确测定。因此经典力学的定律一般只是宏观物体低速运动时的近似定律。
【牛顿力学】它是以牛顿运动定律为基础,在17世纪以后发展起来的。直接以牛顿运动定律为出发点来研究质点系统的运动,这就是牛顿力学。它以质点为对象,着眼于力的概念,在处理质点系统问题时,须分别考虑各个质点所受的力,然后来推断整个质点系统的运动。牛顿力学认为质量和能量各自独立存在,且各自守恒,它只适用于物体运动速度远小于光速的范围。牛顿力学较多采用直观的几何方法,在解决简单的力学问题时,比分析力学方便简单。
【分析力学】经典力学按历史发展阶段的先后与研究方法的不同而分为牛顿力学及分析力学。1788年拉格朗日发展了欧勒·达朗伯等人的工作,发表了“分析力学”。分析力学处理问题时以整个力学系统作为对象,用广义坐标来描述整个力学系统的位形,着眼于能量概念。在力学系统受到理想约束时,可在不考虑约束力的情况下来解决系统的运动问题。分析力学较多采用抽象的分析方法,在解决复杂的力学问题时显出其优越性。
【理论力学】是力学与数学的结合。理论力学是数学物理的一个组成部分,也是各种应用力学的基础。它一般应用微积分、微分方程、矢量分析等数学工具对牛顿力学作深入的阐述并对分析力学作系统的介绍。由于数学更深入地应用于力学这个领域,使力学更加理论化。
【运动学】用纯粹的解析和几何方法描述物体的运动,对物体作这种运动的物理原因可不考虑。亦即从几何方面来研究物体间的相对位置随时间的变化,而不涉及运动的原因。
【动力学】讨论质点系统所受的力和在力作用下发生的运动两者之间的关系。以牛顿定律为基础,根据不同的需要提出了各种形式的动力学基本原理,如达朗伯原理、拉格朗日方程、哈密顿原理、正则方程等。根据系统现时状态以及内部各部分间的相互作用和系统与它周围环境之间的相互作用可预言将要发生的运动。
【弹性力学】它是研究弹性体内由于受到外力的作用或温度改变等原因而发生的应力,形变和位移的一门学科,故又称弹性理论。弹性力学通常所讨论的是理想弹性体的线性问题。它的基本假定是:物体是连续、均匀和各向同性的;物体是完全弹性体;在施加负载前,体内没有初应力;物体的形变十分微小。根据上述假定,对应力和形变关系而作的数学推演常称为数学弹性力学。此外还有应用弹性力学。如物体形变不是十分微小,可用非线性弹性理论来研究。若物体内部应力超过了弹性极限,物体将进入非完全弹性状态。此时则必须用塑性理论来研究。
【连续介质力学】它是研究质量连续分布的可变形物体的运动规律,主要讨论一切连续介质普遍遵从的力学规律。例如,质量守恒、动量和角动量定理、能量守恒等。弹性体力学和流体力学有时综合讨论称为连续介质力学。
【力】物体之间的相互作用称为“力”。当物体受其他物体的作用后,能使物体获得加速度(速度或动量发生变化)或者发生形变的都称为“力”。它是物理学中重要的基本概念。在力学的范围内,所谓形变是指物体的形状和体积的变化。所谓运动状态的变化指的是物体的速度变化,包括速度大小或方向的变化,即产生加速度。力是物体(或物质)之间的相互作用。一个物体受到力的作用,一定有另一个物体对它施加这种作用,前者是受力物体,后者是施力物体。只要有力的作用,就一定有受力物体和施力物体。平常所说,物体受到了力,而没指明施力物体,但施力物体一定是存在的。不管是直接接触的物体间的力,还是间接接触的物体间的力作用;也不管是宏观物体间的力作用,还是微观物体间的力作用,都不能离开物体而单独存在。力的作用与物质的运动一样要通过时间和空间来实现。而且,物体的运动状态的变化量或物体形态的变化量,取决于力对时间和空间的累积效应。根据力的定义,对任何一个物体,力与它产生的加速度方向相同,它的大小与物体所产生的加速度成正比。且两力作用于同一物体所产生的加速度,是该两力分别作用于该物体所产生的加速度的矢量和。
力是一个矢量,力的大小、方向和作用点是表示力作用效果的重要特征,称它为力的三要素。力的合成与分解遵守平行四边形法则。在国际单位制(SI)中,规定使质量为1千克的物体,产生加速度为1米/秒2的力为1牛顿,符号是N。(1千克力=9.80665牛顿。1牛顿=105达因)
力的种类很多。根据力的效果来分的有压力、张力、支持力、浮力、表面张力、斥力、引力、阻力、动力、向心力等等。根据力的性质来分的有重力、弹力、摩擦力、分子力、电磁力、核力等等。在中学阶段,一般分为场力(包括重力、电场力、磁场力等),弹力(压力、张力、拉力等),摩擦力(静摩擦力、滑动摩擦力等)。
【力的三要】力的大小、方向和作用点合称为“力的三要素”。常用有向线段来表示力。线段的长度跟力的大小成正比,箭头表示力的方向,线段的起点表示力的作用点。用上述方式表示力叫“力的图示法”。当考虑有关力的问题时,必须考虑这三个要素。
【物性】是物理学的内容之一,是研究有关物质的气、液、固三态的力学和热学性质的科学。物性学原指研究物质三态的机械性质和热性质的学科。随着对物质性质的研究,逐渐由力学和热学扩展到电磁学、光学等方面,物性学所涉及的范围太广,现已不再作为一门单独的学科,而将其内容分别纳入有关的学科。
【物理变化】指物质的状态虽然发生了变化,但一般说来物质本身的组成成分却没有改变。例如:位置、体积、形状、温度、压强的变化,以及气态、液态、固态间相互转化等。还有物质与电磁场的相互作用,光与物质的相互作用,以及微观粒子(电子、原子核、基本粒子等)间的相互作用与转化,都是物理变化。
【物质】物质为构成宇宙间一切物体的实物和场。例如空气和水,食物和棉布,煤炭和石油,钢铁和铜、铝,以及人工合成的各种纤维、塑料等等,都是物质。世界上,我们周围所有的客观存在都是物质。人体本身也是物质。除这些实物之外,光、电磁场等也是物质,它们是以场的形式出现的物质。
物质的种类形态万千,物质的性质多种多样。气体状态的物质,液体状态的物质或固体状态的物质;单质、化合物或混合物;金属和非金属;矿物与合金;无机物和有机物;天然存在的物质和人工合成的物质;无生命的物质与生命物质以及实体物质和场物质等等。物质的种类虽多,但它们有其特性,那就是客观存在,并能够被观测,以及都具有质量和能量。
【物体】由物质构成的,占有一定空间的个体都称为物体。通过人类感觉器官可感觉到它存在的客观现实。
【张力】被拉伸的弦、绳等柔性物体对拉伸它的其他物体的作用力或被拉伸的柔性物体内部各部分之间的作用力。例如,某绳AB可以看成是AC和CB两段组成,其中C为绳AB中的任一横截面,AC段和CB段的相互作用力就是张力。在绳的截面上单位面积所受的张力称为张应力。
【力的单位】在米·千克·秒制中力的单位是“牛顿”。力的大小,习惯上用重力的单位。若在弹簧秤上挂500克的砝码时的伸长长度与用手拉弹簧秤的伸长长度相同时,手的拉力便与500克砝码的重力大小相同。因此,与500克的重量同样作用的力,就用500克的力来表示。但实际上,克、千克都是质量的单位,克重或千克重等重量单位是属于力的一种重力单位,不能代表全部,而且在计算上数值不同,故有力之绝对单位。依牛顿力学的定义:力=质量×加速度。质量为1千克的质点,在力的方向产生1米/秒2的加速度时,则称该力为1千克·米/秒2=1牛顿。因质点受地球引力作用,下落时的重力加速度为g=9.8米/秒2,故质量为1千克的质点的重力G=mg=1×9.8千克·米/秒2=9.8牛顿。
【牛顿】它是国际单位制中力的单位。使质量是1千克的物体获得1米·秒-2加速度的力叫作1“牛顿”。符号用N表示。(1牛顿=105达因)。
【重力】地球对物体的引力称为“重力”。关于重力有各种不同的解释,如,是一个物体在宇宙中受到其他物体万有引力作用的总合;重力即地球对物体的吸引力;重力是由于地球的吸引而使物体受到的力;宇宙中的每个质点与其他质点之间,都存在着一种引力性的相互作用,与两质点质量的乘积成正比,与其间距离的平方成反比,这种相互作用力称为“重力”。
上述几种讲法虽略有区别,但强调了它们的本质是引力。因为处于引力场的物体都受到重力,重力的本质是引力相互作用。地面附近的物体,由于其他天体距离它很远,地球上其他物体对它的万有引力很小,所以该物体的重力是指地球对它的万有引力,其方向指向地心。离地面愈远,重力愈小。同一物体在地球上不同地点重力也稍有不同,从赤道到两极重力是逐渐增加的,因为地球是一个扁球体,其赤道处半径大于两极处半径。地球上的物体随地球的自转而作匀速圆周运动,作匀速圆周运动的物体所需的向心力,来源于地球对物体的引力。向心力与重力同为引力的分力。由于地球上各地的地形与地质构造不同,物体在地球上不同的地点引力将有所变化,而物体的重力也随之而变化。利用这种重力的变化可以探矿(可探测煤、铁、铜矿及石油的蕴藏量等)。
【重量】按照我国法定计量单位的规定,重量仅作为质量的一种习惯性称呼。在物理学界过去有一种提法是:在地球表面附近,物体所受重力的大小,称为“重量”。地球表面上的物体,除受地球对它的重力作用外,由于地球的自转,还将受到惯性离心力的作用,这两个力的合力的大小称为该物体的重量。习惯上人们认为:物体所受到的重力就是它本身的重量。对重量的解释有许多说法,例如,重量就是重力;物体的重量就是地球对该物体的万有引力;重量即物体所受重力的大小;重量是物体静止时,拉紧竖直悬绳的力或压在水平支持物上的力。
上述几种讲法,有的强调重量即重力,是矢量,它们的本质是引力。有的强调重力不是矢量,重量是重力的大小,是标量。还有的是以测量法则作为重量的定义。这些不同的定义只是解释的不同而已,谈不到对与错。
质量为1千克的物体,在纬度45°的海平面上所受的重力即重量称为1千克力。不同的物体重量不同,同一物体在地球上的位置不同,它的重量也有差异。1千克的物体,在赤道上称得重量是0.9973千克力,而在北极称之则是1.0026千克力。同一物体所处位置不同,其质量不变,而重量则愈近两极和愈近地面则愈大。
【重心】物体各部分所受重力的合力的作用点。在物体内各部分所受重力可看作是一组同向平行力,不管该物体在重力场中如何放置,这些平行力的合力水远通过物体上的某一固定点,该点就是物体的“重心”。均匀物体的重心,只跟物体的形状有关。有规则形状的均匀物体,它的重心就在几何中心上。例如,均匀直棒的重心在棒之中央;均匀球体的重心在球心;三角板的重心在三角形三条中线的交点;正方形的重心在两对角线的交点;立方体的重心在中心。不均匀物体的重心的位置,除跟物体的形状有关外,还跟物体内部质量的分布有关。例如,载货汽车的重心随载货的多少,以及装车的位置而不同;起重机的重心是随着提升物体的重力和高度而变化。对一般物体求重心可用悬线法,用线悬挂物体,在平衡时,合力的作用点(重心)一定在悬挂线的延长线上,然后把悬挂点换到物体上的另一点,再使它平衡,则重心一定也在新的悬挂线的延长线上,前后两线的交点就是重心的位置。
【质量】物理学中基本概念之一,在牛顿定律中质量的概念是作为物体的惯性的量度而提出的。在牛顿第二定律中,关于“质量”的阐述是:若作用力不变,那么物体获得的加速度与它的质量成反比。这一质量是物体惯性大小的量度,称之为“惯性质量”。物体A和B的惯性质量mAmB之比,定义为在同一作用力下它们所获得的加速度aA和aB的反比,即
mA∶mB=aB∶aA
用一选定的标准体为惯性质量的标准,其他物体的惯性质量的大小,可根据上述关系式,用测量加速度的办法与标准体的惯性质量加以比较来求出。
物体都是引力场的源泉,都能产生引力场,也都受引力场的作用。通过万有引力定律将物体的这一属性表现出来:
![]()
![]()
其中m1和m2代表两个物体各自产生引力场和受引力场作用的本领,也叫做两物体各自的“引力质量”。r代表两物体间的距离,F是作用于两个物体间的万有引力,G是一个常数,其大小由选择F、r、m1和m2的单位而定。由万有引力定律公式知,物体A和B的引力质量m′A和m′B之比,定义为它们各自与另一物体的万有引力FA和FB之比,即
m′A∶m′B=FA∶FB
所以用测得引力的方法,可把一待测物体的引力质量与一标准体的引力质量加以比较的方法来测量引力质量。这就是用天平来测物体质量的办法。所以说,天平测的是引力质量的大小。
同种物质质量的大小和该物质的多少成正比,有时亦可将质量定义为:物体所含物质的多少。后来质量的值一般用物体所受外力和由此得到的加速度之比来表示。在同样外力作用下,惯性较大的物体得到的加速度较小,也就是它的质量较大。当物体作高速(即其速度v接近光在真空中的速度c)运动时,物体的质量m与其速度v有关,其关系为

“静止质量”。根据这一关系式,质量随速度的增大而增加,但只有v接近光速c时才显著,通常v比c小得多,m和m0相差很微小,故质量可看作是一个不变的恒量。由于惯性质量同它的引力质量在数值上相等,故在物理学中,惯性质量和引力质量统称为质量。
【质量和重力】质量和重力是完全不同的两个物理量,绝不能混淆,现比较如下:
1.定义不同。质量是物体惯性的量度,它是任何物体都固有的一种属性。重力则反映了物体所受地球的吸引力。
2.质量是标量。重力是矢量。
3.牛顿力学中的质量是一个恒量,重力则随物体所处的纬度和高度的不同而变化。质量为1千克的物体,只有在纬度45°的海平面上重量才是1千克,这个千克后面加个“力”字,与质量的千克加以区别。若将这个物体放在赤道,它的重力为0.9973千克力;放在北极,它的重量则是1.0026千克力。
物体无论是否受到重力的作用,它总是具有质量的。例如,宇宙飞船远离地球,摆脱了地球的引力,就无所谓重力了,但物体的质量仍然存在。当关掉发动机之后,宇宙飞船,仍能凭借惯性继续飞行,这说明物体的质量仍在起作用。
4.质量用天平测定。重力则用弹簧秤测之。其原因是:天平是等臂杠杆。设臂长为L,被测物体的重力是W1,砝码的重力是W2。当天平平衡时,根据杠杆平衡原理得到
W1L=W2L
W1=W2
所以,当天平平衡时,物体与砝码的重力是相等的。由于物体和砝码在地球上的同一地点,设此地的重力加速度为g,则W1=m1g,W2=m2g。
因此,m1g=m2g
m1=m2
从上式知,一个物体无论在地球上任何地方,用天平来称量,物体的质量总是等于跟它平衡的砝码的质量。由砝码的质量数,就能知道物体的质量数。在地球表面,用天平测出物体质量数,就可近似认为与重力数相等。但要知重力的精确数,就必须知道该地的重力加速度,而后根据天平所测知的物体质量m,算出物体的重力(G=mg)。
用弹簧秤来称量物体,由于弹簧的伸长与作用力成正比,所以从弹簧秤的刻度上就可读出物体的重力数值。我国历来所用的杆秤实际上是不等臂的天平,因此用它测物体时,是质量而不是重力。
5.质量和重力的单位
在国际单位制里,质量的单位是千克,重力的单位是牛顿。实用时,重力的单位常用千克力或克力。
综上所述,质量和重力的本质是两个不同的物理量,但它们又有密切的联系,是通过牛顿第二定律公式F=ma建立起来的。物体自由下落,其重力加速度由物体所受的重力产生。若物体质量为m,受到的重力为G,重力加速度为g,根据F=ma,得G=mg,这就是质量和重力的关系式。由此可看出:在地球上同一地点,g为常量,重力与质量成正比。在地球上不同地点,重力加速度稍有不同,因此重力也稍有差异。利用公式G=mg算出的重力,在国际单位制中是以牛顿为单位的。
【密度】某种物质的质量和其体积的比值,即单位体积的某种物质
![]() 位制中,质量的主单位是千克,体积的主单位是立方米,于是取1立方米物质的质量作为物质的密度。对于非均匀物质则称为“平均密度”。地球的平均密度为5.5×103千克/米3,标准状况下干燥空气的平均密度为0.001293×103千克/米3。常见的非金属固体、金属、液体、气体的密度见附表。
位制中,质量的主单位是千克,体积的主单位是立方米,于是取1立方米物质的质量作为物质的密度。对于非均匀物质则称为“平均密度”。地球的平均密度为5.5×103千克/米3,标准状况下干燥空气的平均密度为0.001293×103千克/米3。常见的非金属固体、金属、液体、气体的密度见附表。
密度在生产技术上的应用,可从以下几个方面反映出来。
1.可鉴别组成物体的材料。
2.可计算物体中所含各种物质的成分。
3.可计算某些很难称量的物体的质量。
4.可计算形状比较复杂的物体的体积。
5.可判定物体是实心还是空心。
6.可计算液体内部压强以及浮力等。
综上所述,可见密度在科学研究和生产生活中有着广泛的应用。对于鉴别未知物质,密度是一个重要的依据。“氩”就是通过计算未知气体的密度发现的。经多次实验后又经光谱分析,确认空气中含有一种以前不知道的新气体,把它命名为氩。在农业上可用来判断土壤的肥力,含腐殖质多的土壤肥沃,其密度一般为2.3×103千克/米3。根据密度即可判断土壤的肥力。在选种时可根据种子在水中的沉、浮情况进行选种:饱满健壮的种子因密度大而下沉;瘪壳和其他杂草种子由于密度小而浮在水面。在工业生产上如淀粉的生产以土豆为原料,一般来说含淀粉多的土豆密度较大,故通过测定土豆的密度可估计淀粉的产量。又如,工厂在铸造金属物之前,需估计熔化多少金属,可根据模子的容积和金属的密度算出需要的金属量。
【比重】物体的重力和它的体积的比值,即单位体积的某种物质的重力,称作该物体的“比重”。用γ表示比重,G表示重力,V表示体
![]()
除气体外,任何物质某体积的重力,和4℃时同体积的水的重力相比,即称为该物质的比重。物质的重力和其质量成正比,则其单位体积的重力,必和其密度成正比,所以任何物质的比重,又等于该物质和水在4℃的密度相比。列式如下。
![]()
![]()
气体以外各种物质的比重皆以水为共同标准,而用C·G·S单位制时,水的密度在4℃时适等于1克/厘米3,故物质的比重常和其密度的数值相等。唯密度须以1克/厘米3为单位,比重则仅为纯数字,所以意义上绝不相同。简言之,即比重是一单位容积物质和同一单位水的相对密度。根据1978年国际纯粹应用物理学协会所属符号单位和术语委员会的文件建议,我国已取消比重的概念,而以密度的概念代替。
【弹力】亦称“弹性力”。物体受外力作用发生形变后,若撤去外力,物体能回复原来形状的力,叫作“弹力”。它的方向跟使物体产生形变的外力的方向相反。因物体的形变有多种多样,所以产生的弹力也有各种不同的形式。例如,一重物放在塑料板上,被压弯的塑料要恢复原状,产生向上的弹力,这就是它对重物的支持力。将一物体挂在弹簧上,物体把弹簧拉长,被拉长的弹簧要恢复原状,产生向上的弹力,这就是它对物体的拉力。不仅塑料、弹簧等能够发生形变,任何物体都能够发生形变,不发生形变的物体是不存在的。不过有的形变比较明显,能直接见到;有的形变相当微小,必须用仪器才能觉察出来。
【形变】凡物体受到外力而发生形状变化谓之“形变”。物体由于外因或内在缺陷,物质微粒的相对位置发生改变,也可引起形态的变化。形变的种类有:
1.纵向形变:杆的两端受到压力或拉力时,长度发生改变;
2.体积形变:物体体积大小的改变;
3.切变:物体两相对的表面受到在表面内的(切向)力偶作用时,两表面发生相对位移,称为切变;
4.扭转:一圆柱状物体,两端各受方向相反的力矩作用而扭转,称扭转形变;
5.弯曲:两端固定的钢筋,因负荷而弯曲,称弯曲形变。
无论产生什么形变,都可归结为长变与切变。
【测力计】利用金属的弹性制成标有刻度用以测量力的大小的仪器,谓之“测力计”。测力计有各种不同的构造形式,但它们的主要部分都是弯曲有弹性的钢片或螺旋形弹簧。当外力使弹性钢片或弹簧发生形变时,通过杠杆等传动机构带动指针转动,指针停在刻度盘上的位置,即为外力的数值。有握力计等种类,而弹簧秤则是测力计的最简单的一种。
【弹簧秤】弹簧秤又叫弹簧测力计,是利用弹簧的形变与外力成正比的关系制成的测量作用力大小的装置。
弹簧秤分压力和拉力两种类型,压力弹簧秤的托盘承受的压力等于物体的重力,秤盘指针旋转的角度指示所受压力的数值。拉力弹簧秤的下端和一个钩子连在一起(这个钩子是与弹簧下端连在一起的),弹簧的上端固定在壳顶的环上。将被测物挂在钩上,弹簧即伸长,而固定在弹簧上的指针随着下降。由于在弹性限度内,弹簧的伸长与所受之外力成正比,因此作用力的大小或物体重力可从弹簧秤的指针指示的外壳上的标度数值直接读出。
在使用时应注意所测的重力或力不要超过弹簧秤的量度范围,还应检查,在弹簧秤未挂物体时指针是否指在零刻度,若不在零刻度可进行修正。此外还应注意勿使弹簧和指针跟外壳摩擦,以免误差过大。
【胡克定律】力学基本定律之一。适用于一切固体材料的弹性定律。它指出:在弹性限度内,物体的形变跟引起形变的外力成正比。这个规律是英国物理学家胡克于1660年发现的(1670年发表),故叫作“胡克定律”。该定律对拉伸(或压缩)形变的具体表述为:在弹性限度内,
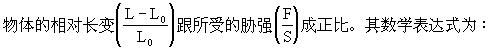
![]()
长度,F为物体所受的外力,S为物体横截面的面积,α为物体的伸长
![]()
![]()
比例常数,叫做弹簧的倔强系数。它是一个有单位的量。在国际单位制中,f的单位是牛,x的单位是米,它是形变量(弹性形变),k的单位是牛/米。倔强系数在数值上等于弹簧伸长(或缩短)单位长度时的弹力。
【弹性力】物体发生弹性形变后,内部产生企图恢复形变的力称为“弹性力”,或“弹力”。见弹力条。
【弹性】物体在外力作用下产生形变,撤去外力,形变立即消失而恢复其原来形状和大小的性质谓之“弹性”。
【弹性限度】亦称“弹性极限”。物体受到外力作用,在内部所产生的抵抗外力的相互作用力不超过某一极限值时,若外力作用停止,其形变可全部消失而恢复原状,这个极限值称为“弹性限度”。使物体发生形变的力若超过该值即使外力撤消,物体也不能完全恢复原状。例如,用力拉一弹簧,若拉力不太大时,在拉力撤消时,弹簧即能恢复原来状态;若拉力超过某一数值,弹簧就不能恢复原来状态。这个数值(最大极限)即为弹性限度。
【弹性形变】固体受外力作用而使各点间相对位置的改变,当外力撤消后,固体又恢复原状谓之“弹性形变”。若撤去外力后,不能恢复原状,则称为“范性形变”。因物体受力情况不同,在弹性限度内,弹性形变有四种基本类型:即拉伸和压缩形变;切变;弯曲形变和扭转形变。
【弯曲形变】物体发生弯曲时产生的形变叫做“弯曲形变”。物体弯曲得越厉害,产生的弹力就越大。例如,将弓拉得越满,箭就射得越远。把一个物体放在支持物上,物体越重,支持物被压弯曲得越厉害,支持力就越大。
【扭转形变】在金属丝的下面挂一个横杆,用力扭转这个横杆,金属丝就发生扭转形变,手放开,发生扭转形变的金属丝产生的弹力会把横杆扭回来。金属丝的扭转角度越大,弹力就越大。这种由于物体发生扭转而产生的形变叫做“扭转形变”。
【倔强系数】它是一个有单位的量。用k来表示,单位是牛/米。倔强系数在数值上等于弹簧伸长(或缩短)单位长度时的弹力。倔强系数跟弹簧的长度、弹簧的材料、弹簧丝的粗细等等都有关系。弹簧丝粗的硬弹簧比弹簧丝细的软弹簧倔强系数大。
【摩擦】当物体与另一物体沿接触面的切线方向运动或有相对运动的趋势时,在两物体的接触面之间有阻碍它们相对运动的作用力,这种力叫摩擦力。接触面之间的这种现象或特性叫“摩擦”。摩擦有利也有害,但在多数情况下是不利的,例如,机器运转时的摩擦,造成能量的无益损耗和机器寿命的缩短,并降低了机械效率。因此常用各种方法减少摩擦,如在机器中加润滑油等。但摩擦又是不可缺少的,例如,人的行走,汽车的行驶都必须依靠地面与脚和车轮的摩擦。在泥泞的道路上,因摩擦太小走路就很困难,且易滑倒,汽车的车轮也会出现空转,即车轮转动而车厢并不前进。所以,在某些情况下又必须设法增大摩擦,如在太滑的路上撒上一些炉灰或沙土,车轮上加挂防滑链等。
【摩擦力】相互接触的两物体在接触面上发生的阻碍该两物体相对运动的力,谓之“摩擦力”。另有两种说法是:一个物体沿着另一个物体表面有运动趋势时,或一个物体在另一个物体表面滑动时,都会在两物体的接触面上产生一种力,这种力叫做摩擦力;相互接触的两个物体,如果有相对运动或相对运动的趋势,则两物体的接触表面上就会产生阻碍相对运动趋势的力,这种力叫做摩擦力。
按上述定义,产生摩擦力的条件,可分为静摩擦力、滑动摩擦力。两个接触着的物体,有相对滑动的趋势时,物体之间就会出现一种阻碍起动的力,这种力叫静摩擦力。两个接触着的物体,有了沿接触面的相对滑动,在接触面上就会产生阻碍相对滑动的力,这种力叫做滑动摩擦力。因此不能把摩擦力只看作是一种阻力。有时可以是动力。例如,放在卡车上的货物,是随卡车一起加速运动时,货物受到的静摩擦力,是阻碍它和卡车相对滑动趋势的,但却是它获得加速度的动力。若卡车有足够大的加速度,货物与卡车之间就出现了相对滑动,这时货物受到的滑动摩擦力,就是阻碍它和卡车做相对滑动的,但摩擦力仍是货物作加速运动的动力。
滑动摩擦力总是与物体滑动的方向相反。但是,静摩擦力是阻碍两个物体发生相对滑动的力,到底与物体相对运动的方向(以地球作参照物)是相同还是相反,应看问题的性质来定。例如,货物在传送带上随皮带一起以一定速度作匀速直线运动。货物与皮带的速度相同,没有相对运动趋势,所以货物与皮带之间没有产生静摩擦力。当皮带作加速运动时,货物所受的静摩擦力的方向(以地球作参照系)与运动的方向是相同的。若皮带作减速运动,皮带对货物的静摩擦力方向与运动方向相反。
摩擦力的大小,跟相互接触物体的性质,及其表面的光滑程度有关,和物体间的正压力有关,一般地说,和接触面积无关。一般情况下,当两物体相接触挤压时,两者实际接触部分,远小于两者的表观接触面积。经研究表明:两者实际接触部分的面积越大,其摩擦力也越大。而两者的实际接触面积只跟正压力的大小、物体表面的粗糙程度和材料的性质有关,跟它们的表观接触面积无关。在物体表面粗糙程度和材料性质不变的情况下,正压力越大,实际接触面积也越大,摩擦力也越大;正压力相同时,改变物体间的表观接触面积,例如,将平面上的砖从竖放改变为平放,并不改变实际的压力,摩擦力保持不变。因此,在一般情况下,摩擦力跟物体的表观接触面积无关。
【静摩擦】置于固定平面上的物体由于受沿它们接触表面切向的外力作用有相对滑动的趋势但还没有发生相对滑动的时候,存在于接触表面的阻碍这种滑动趋势的现象,谓之“静摩擦”。这里应注意两点:一是两个紧密接触而又相对静止的物体;另一点是具有相对滑动的趋势,但又还没有发生相对的滑动。
【静摩擦力】当物体与另一物体沿接触面的切线方向运动或有相对运动的趋势时,在两物体的接触面之间有阻碍它们相对运动的作用力,这个力叫摩擦力。若两相互接触,而又相对静止的物体,在外力作用下如只具有相对滑动趋势,而又未发生相对滑动,则它们接触面之间出现的阻碍发生相对滑动的力,谓之“静摩擦力”。当切向外力逐渐增大但两物体仍保持相对静止时,静摩擦力随着切向外力的增大而增大,但静摩擦力的增大只能到达某一最大值。静摩擦力f在达到最大值以前,总跟物体所受沿着接触面切向方向的外力大小相等,方向相反。
【最大静摩擦力】在静摩擦中出现的摩擦力称为静摩擦力。当切向外力逐渐增大但两物体仍保持相对静止时,静摩擦力随着切向外力的增大而增大,但静摩擦力的增大只能到达某一最大值。当切向外力的大小大于这个最大值时,两物体将由相对静止进入相对滑动。静摩擦力的这个最大值称为“最大静摩擦力”。这个极限摩擦力,以,f最大表示。最大静摩擦力的大小与两物体接触面之间的正压力N成正比,即
f0max=μ0N
用f0max表示最大静摩擦力,N表示正压力,其中比例常数μ0叫做静摩擦系数,是一个没有单位的数值。μ0和接触面的材料、光滑粗糙程度、干湿情况等因素有关,而与接触面的大小无关。
【静摩擦系数】见”最大静摩擦力”。
【动摩擦】两个相接触的物体做相对运动时发生的阻碍它们相对运动的现象,称为“动摩擦”。
【动摩擦力】在动摩擦中出现的摩擦力称为“动摩擦力”。对物体所施之力大于最大静摩擦力时,物体就开始运动。在运动起来之后,若将所施加之力减小,物体便又停止运动。这一情况表明,物体运动之后,还有阻止物体运动的力,即还有摩擦阻力。这种物体运动时所产生的摩擦力即称动摩擦力。
【动摩擦系数】动摩擦力的大小与正压力大小之比称为“动摩擦系数”。公式中μ是比例系数,其值与相接触两物体的材料和表面粗糙程度有关。
【滑动摩擦】当一物体在另一物体表面上滑动或有滑动趋势时,在两物体接触面上产生的阻碍它们之间相对滑动的现象,谓之“滑动摩擦”。当物体间有相对滑动时的滑动摩擦称动摩擦。当物体间有滑动趋势而尚未滑动时的滑动摩擦称为静摩擦。滑动摩擦产生的原因很复杂,目前还没有定论。近代摩擦理论认为,产生滑动摩擦的主要原因有二,一是关于摩擦的凹凸啮合说,认为摩擦的产生是由于物体表面粗糙不平。当两个物体接触时,在接触面上的凹凸不平部分就互相啮合,而使物体运动受到阻碍而引起摩擦;二是分子粘合说,认为当相接触两物体的分子间距离小到分子引力的作用范围内时,在两个物体紧压着的接触面上的分子引力便引起吸附作用。关于摩擦的本质,还待进一步研究。
【滑动摩擦力】物体沿着接触面作相对滑动时,两物体的接触面上相互作用,阻碍滑动的力叫“滑动摩擦力”。它的方向总是和物体相对滑动的方向相反。滑动摩擦力的大小和彼此接触物体的相互间的正压力成正比,在相对运动速度较低时几乎与速度的变化无关,且小于最大静摩擦力。
【滑动摩擦系数】滑动摩擦力的大小和彼此接触物体的相互间的正压力成正比:即f=μN,其中μ为比例常数叫“滑动摩擦系数”,它是一个没有单位的数值。滑动摩擦系数与接触物体的材料、表面光滑程度、干湿程度、表面温度、相对运动速度等都有关系。
【滚动摩擦】一物体在另一物体表面作无滑动的滚动或有滚动的趋势时,由于两物体在接触部分受压发生形变而产生的对滚动的阻碍作用,叫“滚动摩擦”。滚动摩擦一般用阻力矩来量度,其力的大小与物体的性质、表面的形状以及滚动物体的重量有关。滚动摩擦实际上是一种阻碍滚动的力矩。当一个物体在粗糙的平面上滚动时,如果不再受动力或动力矩作用,它的运动将会逐渐地慢下来,直到静止。这个过程,滚动的物体除了受到重力、弹力外,一般在接触部分受到静摩擦力。由于物体和平面接触处产生形变,物体受重力作用而陷入支承面,同时物体本身也受压缩而变形,当物体向前滚动时,接触处前方的支承面隆起,而使支承面作用于物体的合弹力N的作用点从最低点向前移。正是这个弹力,相对于物体的质心产生一个阻碍物体滚动的力矩,这就是滚动摩擦。对于初中学生来说,他们还未掌握力矩的概念,就不要把滚动摩擦讲成是一种摩擦力,只能讲一个物体在另一个物体上滚动时所受到对滚动的阻碍作用。
【滚动摩擦力】物体滚动时,接触面一直在变化着,物体所受的摩擦力,称为“滚动摩擦力”。它实质上是静摩擦力。接触面愈软,形状变化愈大,则滚动摩擦力就愈大。一般情况下,物体之间的滚动摩擦力远小于滑动摩擦力。在交通运输以及机械制造工业上广泛应用滚动轴承,就是为了减少摩擦力。例如,火车的主动轮的摩擦力是推动火车前进的动力。而被动轮所受之静摩擦则是阻碍火车前进的滚动摩擦力。
【滚动摩擦系数】物体在另一物体上滚动(或有滚动趋势)时受到的阻碍作用是由物体和支承面接触处的形变而产生的。一般用滚动摩擦力矩来量度。滚动摩擦力矩的大小和支承力N成正比。即M=KN。K为比例系数,称为“滚动摩擦系数”。如火车轮与铁轨间的K值约为0.09~0.03厘米。圆轮和支持面愈坚硬,则滚动摩擦愈小。若两者为绝对刚体,则滚动摩擦就为零。此时,轮与支持面间只接触一条线,支承力N通过圆轮的轴心。滚动摩擦系数具有长度的量纲,且有力臂的意义,常以厘米计算。其大小主要取决于相互接触物体的材料性质和表面状况(粗糙程度,湿度等)有关。
【牛顿第一定律】任何物体,在不受外力作用时,总保持静止状态或匀速直线运动状态,直到其他物体对它施加作用力迫使它改变这种状态为止,这就是“牛顿第一定律”。该定律说明力并不是维持物体运动的条件,而是改变物体运动状态的原因。牛顿第一定律亦称“惯性定律”。它科学地阐明了力和惯性这两个物理概念,正确地解释了力和运动状态的关系,并提出了一切物体都具有保持其运动状态不变的性质——惯性,它是物理学中一条基本定律。上述定律主要是从天文观察中,间接推导而来,是抽象概括的结论,不能单纯按字面定义而用实验直接验证。和实际情况较接近的说法是:任何物体在所受外力的合力为零时,都保持原有的运动状态不变。即原来静止的继续静止,原来运动的继续作匀速直线运动。物体的惯性实质是物体相对于平动运动的惯性,其大小即为惯性质量。物体相对于转动也有惯性,但它跟第一定律所说的惯性不是一回事,它的大小为转动惯量。惯性质量和转动惯量都用来表示惯性,但它们是不同的物理量,中学物理不出现转动惯量的名词,可不必提两者的区别。物体在没有受到外力作用或所受合外力为零的情况下,究竟是静止还是作匀速直线运动,这除了和参考系有关外,还要看初始时的运动状态。
【牛顿第二定律】牛顿第二定律的一般表述为:物体运动的加速度a的大小与其所受合力的大小成正比,与其质量m成反比,加速度a的方向与所受合力F的方向相同。其表示式为
F=kma
式中k是比例系数,其数值决定于力、质量和加速度的单位。在国际单位制中即米·千克·秒制中的k为1。上式成为
F=ma
即作用于该物体上各力的合力F等于物体的质量m与在该力作用下所产生的加速度a的乘积。这里所指的物体是质点。
合外力的方向决定了物体加速度的方向,加速度的方向反映了物体所受的合外力的方向。加速度和合外力是即时相对应的。物体在每一时刻的即时加速度,是跟那一时刻所受的合外力成正比的。恒力产生恒定的加速度,变力产生变加速度,当力的作用消失,则加速度也即消失。物体在合外力作用下如何运动,则视合外力是恒力还是变力,以及初始运动状态而定。
牛顿第二定律只适用于解决物体的低速运动问题,不能用以处理高速运动问题;只适用于宏观物体,一般不适用于微观粒子。应用牛顿第二定律时,一般选用地球或太阳作参照系,且认为地球或太阳本身在作匀速直线运动。
【牛顿第三定律】它是力学中重要的基本定律之一,亦称“作用与反作用定律”。任何物体间的作用力和反作用力同时存在,同时消失,它们的大小相等,方向相反,作用在同一条直线上,但分别作用在两个不同物体上。
作用力与反作用力没有本质的区别,不能认为一个力是起因,而另一个力是结果。两个力中的任何一个力都可以被认为是作用力,而另一个力相对于它就成为反作用力。正确理解作用力和反作用力跟平衡力是有区别的。在低速运动范围,不论是运动物体间还是静止物体间的相互作用;不论是加速运动物体间还是匀速运动物体间的相互作用;不论是短暂的还是持续的相互作用,都遵循牛顿第三定律。
【惯性】物体保持静止或匀速直线运动状态的性质,称为惯性。惯性是物体的一种固有属性,表现为物体对其运动状态变化的一种阻抗程度,质量是对物体惯性大小的量度。当作用在物体上的外力为零时,惯性表现为物体保持其运动状态不变,即保持静止或匀速直线运动;当作用在物体上的外力不为零时,惯性表现为外力改变物体运动状态的难易程度。在同样的外力作用下,加速度较小的物体惯性较大,加速度较大的物体惯性较小。所以物体的惯性,在任何时候(受外力作用或不受外力作用),任何情况下(静止或运动),都不会改变,更不会消失。
【惯性定律】即“牛顿第一运动定律”。
【惯性力】牛顿运动定律只适用于惯性系。在非惯性系中,为使牛顿运动定律仍然有效,常引入一个假想的力,用以解释物体在非惯性系中的运动。这个由于物体的惯性而引入的假想力称为“惯性力”。它是物体的惯性在非惯性系中的一种表现,并不反映物体间的相互作用。它也不服从牛顿第三定律,于是惯性力没有施力物,也没有反作用力。例如,前进的汽车突然刹车时,车内乘客就感觉到自己受到一个向前的力,使自己向前倾倒,这个力就是惯性力。又如,汽车在转弯时,乘客也会感到有一个使他离开弯道中心的力,这个力即称“惯性离心力”。
【惯性系】即惯性参照系的简称。凡牛顿惯性定律能成立的参照系,称“惯性参照系”。对惯性系相对静止或作匀速直线运动的一切参照系都是惯性系。太阳是一个惯性系,若以太阳作参照系时牛顿运动定律总是精确成立的。但太阳系里的所有行星,由于它们的自转与公转,都在作变速运动,所以都不是惯性系。地球是行星之一,当然也不例外,若以地球为参照系,将与牛顿定律不符。由于地球相对太阳运动的加速度很小,故在一些物理问题的讨论中,可近似地把地球看作是一个相当好的惯性系。
【合力】如果几个力同时作用于一个物体,它们对物体运动产生的效果与另一个力单独对物体运动产生的效果相同,则这个力就是它们的“合力”。
【分力】如果一个力作用于某一物体,对物体运动产生的效果相当于另外的几个力同时作用于该物体时产生的效果,则这几个力就是原先那个作用力的分力。例如,拉一置于水平面上的小车前进时,向斜上方所用的拉力可分解为两个分力:一个水平向前使小车前进,另一个垂直向上减少重物对水平面的压力。
【惯性质量】量度物体惯性的物理量。实验发现,在惯性系中,若在两不同物体上施加相同的力,则两物体加速度之比a1/a2是一个常数,与力的大小无关。此结果表明,a1/a2之值仅由该两物体本身的惯性所决定,与其他因素无关。物理学中规定各物体的惯性质量与它们在相同的力作用下获得的加速度数值成反比。若用m1及m2分别表示两物体的惯性质量,则m2/m1=a1/a2。选定其中一物体的惯性质量作为惯性质量的单位后,另一物体的惯性质量可通过实验由上式确定。在国际单位制中,把保存在国际计量局中的国际千克原器的惯性质量作为单位,称为“千克”(其他常用的单位有“吨”、“克”等)。
【引力质量】任何物体都具有吸引其他物体的性质,引力质量是物体这种性质的量度。选定两质点A和B,先后测量它们各自与质点C的引力FAC和FBC。实验发现,只要距离AC和BC相等,则不论这距离的大小如何,也不论质点C是什么物体,力FAC和FBC的比值FAC/FBC是一个常数。该结果表明,FAC/FBC之值仅由质点A和B本身的性质决定。物理学中规定A、B两质点引力质量之比等于力FAC与FBC之比。若用mA及
![]()
的引力质量作为引力质量的单位后,另一质点的引力质量可通过实验由上式确定。通常取保存在国际计量局中的国际千克原器的引力质量为单位,称为“千克”。
【质量守恒】自然界的基本定律之一。在任何与周围隔绝的物质系统(孤立系统)中,不论发生何种变化或过程,其总质量保持不变。18世纪时法国化学家拉瓦锡从实验上推翻了燃素说之后,这一定律始得公认。20世纪初以来,发现高速运动物体的质量随其运动速度而变化,又发现实物和场可以互相转化,因而应按质能关系考虑场的质量。质量概念的发展使质量守恒原理也有了新的发展,质量守恒和能量守恒两条定律通过质能关系合并为一条守恒定律,即质量和能量守恒定律。
质量守恒定律在19世纪末作了最后一次检验,那时候的精密测量技术已经高度发达。结果表明,在任何化学反应中质量都不会发生变化(哪怕是最微小的)。例如,把糖溶解在水里,则溶液的质量将严格地等于糖的质量和水的质量之和。实验证明,物体的质量具有不变性。不论如何分割或溶解,质量始终不变。
在任何化学反应中质量也保持不变。燃烧前炭的质量与燃烧时空气中消耗的氧的质量之和准确地等于燃烧后所生成物质的质量。
【质量守恒定律】即“质量守恒”。见质量守恒条。
【力的合成】一个力,如果它的作用效果跟几个力共同作用时的效果相同,这个力叫做那几个力的合力。求几个力的合力,叫力的合成。在高中物理中,将重点讲共点力的合成共点力。实验证明。两共点力的合成跟速度、加速度的合成一样,服从平行四边形法则。
【共点力】几个力都作用在物体的同一点,或它们的作用线相交于同一点,这几个力便叫做“共点力”。
【平行四边形法则】求两个互成角度的共点力的合力,可以用表示这两个力的线段为邻边作平行四边形,这两个邻边之间的对角线就表示合力的大小和方向,这种方法就叫做“力的平行四边形法则”。
我们知道加、减、乘、除的算术运算,是用来计算两个以上的标量的,如质量、面积、时间等。例如,求密度就要用体积去除质量。标量之间的运算不需要特别的手续,只有一个要求,那就是单位要一致。
但是,矢量相加就要用特别的方法,因为被加的量既有一定数值,又有一定的方向,相加时两者要同时考虑。在力学中经常遇到的矢量有位移、力、速度、加速度、动量、冲量、力矩、角速度和角动量等。
矢量的加法有两种:其一即所谓三角形法则;另一方法即平行四边形法则,它们本质是一样的。若用三角形法则求总位移似乎直观些,而用平行四边形法则求力的合成好像更便于理解。
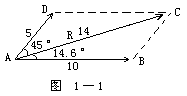
若用3毫米代表1千米。如图1-1所示的那样,以纸面上某点A作为出发点,作矢量 ![]() ,长3厘米,代表向东10公里;然后在A点再作
,长3厘米,代表向东10公里;然后在A点再作 ![]() 同
同 ![]() 成45°角,长1.5厘米,代表向东北5千米。然后,过B作BC平行AD,过D作DC平行AB,由此便得到平行四边形ABCD。从A向C作射线
成45°角,长1.5厘米,代表向东北5千米。然后,过B作BC平行AD,过D作DC平行AB,由此便得到平行四边形ABCD。从A向C作射线
![]() ,这就是总位移矢量。
,这就是总位移矢量。
应注意物体A点不是受 ![]() 、
、 ![]() 、
、 ![]() 三个力的作用。因为
三个力的作用。因为 ![]() 是
是 ![]() 和
和 ![]() 的合力,表示
的合力,表示 ![]() 的作用效果与
的作用效果与
![]() 、
、
![]() 的共同作用效果是一样的。因此可以用
的共同作用效果是一样的。因此可以用 ![]() 代替
代替 ![]() 和
和 ![]() 的共同作用,但绝不能把
的共同作用,但绝不能把 ![]() 当成作用在物体上的第三个力。在分析物体受力情况时,不能同时考虑合力与分力对物体的作用。例如,当物体沿光滑斜面下滑时,不能说物体除受到重力和斜面的弹力作用外,还受到一个下滑力的作用。因为下滑力是重力沿斜面平行方向的分力,所以,只能说“在光滑斜面上下滑的物体,受到重力和斜面弹力的作用”。有的人认为:“合力总比分力大”。我们可利用求合力的平行四边形法则,通过作图可看到,合力的大小是随两分力夹角而变化的,绝不能说“合力一定要比分力大”。
当成作用在物体上的第三个力。在分析物体受力情况时,不能同时考虑合力与分力对物体的作用。例如,当物体沿光滑斜面下滑时,不能说物体除受到重力和斜面的弹力作用外,还受到一个下滑力的作用。因为下滑力是重力沿斜面平行方向的分力,所以,只能说“在光滑斜面上下滑的物体,受到重力和斜面弹力的作用”。有的人认为:“合力总比分力大”。我们可利用求合力的平行四边形法则,通过作图可看到,合力的大小是随两分力夹角而变化的,绝不能说“合力一定要比分力大”。

一个矢量,只要遵守平行四边形法则,可以分解为两个,或无穷个。但是矢量的合成不同,两个矢量只能合成为一个矢量。
【三角形法则】矢量相加的法则,如图1-2。矢量 ![]() 和
和 ![]() 的和是将
的和是将 ![]() 、
、 ![]() 头尾相接,例如,将矢量
头尾相接,例如,将矢量 ![]() 的起点与矢量
的起点与矢量
![]() 的终点相接,此时以
的终点相接,此时以 ![]() 的起点为起点,以
的起点为起点,以 ![]() 的终点为终点的矢量
的终点为终点的矢量 ![]() 就是矢量
就是矢量 ![]() 和
和 ![]() 的矢量和。根据矢量相加的三角形法则求得的矢量和与相加的两矢量的求和次序无关。
的矢量和。根据矢量相加的三角形法则求得的矢量和与相加的两矢量的求和次序无关。
例如,有一艘船,如图1-3所示。由湖中A点先向正北方向航行6千米到了B点,然后航向转了90度,向东再航行了4千米到达C点。航行的总距离是6+4千米,但是出发点到终点的距离(位移的大小)显然小于10千米。
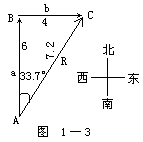
如果要问船在什么地方,离出发点有多远,方位如何,也就是说,我们要求船的总位移,而不是关心船走了多长距离,那么就不能用简单的标量加法去计算了。矢量加法就要用几何作图法,其详细步骤如下:
在纸上先画一条纵向直线AB,长度为6厘米,在B端加一箭头,代表向北走了6千米,即向北的位移为6千米。接着,再由B向右画一横线BC垂直于AB,长度为4厘米,在C端加箭头以表示向东的位移为4千米。最后,把始点A和终点C连起来,加箭头于C端,这就是总的位移矢量
![]() 。用尺量出它的长度,是7.2厘米,按我们上述的比例,它相当于7.2千米。
。用尺量出它的长度,是7.2厘米,按我们上述的比例,它相当于7.2千米。
我们说,向北的位移 ![]() 加上向东的位移
加上向东的位移 ![]() 等于总位移
等于总位移 ![]() ,用矢量形式写出为
,用矢量形式写出为
![]() +
+ ![]() =
= ![]() ,
,
或用黑体字母记为,
a+b=R。
再用一个量角器量出 ![]() 和
和 ![]() 的夹角为33.7°,于是知道合成矢量R偏东与正北成33.7°角。
的夹角为33.7°,于是知道合成矢量R偏东与正北成33.7°角。
在矢量加法中,所有的矢量都用一些带箭头的线段表示,具有一定的长度和方向。不论用多么长的线段来代表单位矢量,都不影响最后结果。
我们也可用几何学和三角学的定理来计算上例船的总位移的大小和方向。
【力的分解】几个力,如果它们产生的效果跟原来一个力产生的效果相同,这几个力就叫做原来那个力的分力。求一个力的分力叫做“力的分解”。分力与合力是矛盾的两个方面,如图1-1所示,相对于AB、AD来说,AC是合力;但是相对于AC来说,AB,AD又是分力。所以,力的分解跟力的合成互为逆运算,在求分力的时候也必须应用平行四边形法则。
下面几个是经常碰到的力的分解问题:
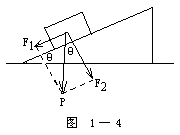
1.斜面上物体重力的分解:如图1-4所示,物体放在倾角为θ的斜面上,将重力P分解为相互垂直的两个分力:一个跟斜面平行的力F1;一个跟斜面垂直的力F2。其中F1=Psinθ,F2=Pcosθ。因斜面上的物体可能静止在斜面上,可能下滑,也可能在外力作用下沿斜面向上运动。无论哪种情况,物体沿斜面运动总跟物体的重力P沿斜面平行的分力F1有关。另外,斜面受到的物体对斜面的正压力又跟物体的重力P沿斜面垂直方向的分力F2有关。故把物体所受的重力分解为跟斜面平行和跟斜面垂直的两个分力。
2.支架受力的分析:如图1-5所示,物体通过绳子挂在O点。物体所受重力产生两个效果,一个是拉斜梁的力F1,一个是压横梁的力F2。已知合力P的大小和方向,以及两分力F1,F2的方向,按平行四边形作图,即可解得F1和F2。

3.帆船逆风行驶的问题:帆船可逆风行驶,船头时而偏左,时而偏右,沿“S”形路线前进。如图1-6(a)所示,MN表示帆面,当逆风吹向MN时,风对帆产生作用力R。因帆对风来说是光滑的,所以作用力R的方向与帆面垂直。把R分解为两个力:一个为与船身垂直的F1,一个为沿船前进方向的F2。显然,分力F1的作用是使船横向移动,但由于船身的侧面积比较大,水的阻力很大,因而船横向移动并不显著。分力F2与船前进方向是一致的,靠着它,船逆着风斜行。当船到达B点后,船头改为偏右,风帆也要相应反转至新的位置。如图1-6(b)所示,船在逆风下将获得一个前进的推力F2。如此反复下去,船将沿“S”形路线逆风前进。

【隔离体法】即“隔离法”。在解力学问题时,若有几个物体一起运动,或一个物体上同时有几个力作用着,为了便于分析物体受力情况,求它们之间的相互作用力,往往把需要的那部分物体从整体中抽出来,单独分析周围物体对它的作用,用力的图示法把作用在物体上的几个力,形象地表示出来。先将所研究的物体与其相联系的物体中“隔离”出来,再把作用在此物体上的力依次画出,并标明力的大小和方向。这种分析物体受力的方法,叫“隔离体法”。应用隔离体法时,应根据题目的内容确定隔离体。着重考虑周围物体对隔离体的作用力,将研究对象的物体隔离出来。要正确运用牛顿第三运动定律,仔细考虑物体之间的相互作用,分析隔离体的受力情况,作出该物体的受力图。应注意不要把力的概念搞乱,例如,正压力、下滑力、张力、支承力、离心力、向心力、浮力、拉力、制动力、牵引力等等,这些力都是重力、弹力、摩擦力这三种基本形式力的不同表现形式。对各被隔离物体,根据牛顿第二运动定律确立力和加速度的关系,分别列出各物体的运动方程。根据题意解联立方程,求出未知量。
【矢量】亦称“向量”。有些物理量,是由数值大小和方向才能完全确定的物理量,这些量之间的运算并不遵循一般的代数法则,在相加减时它们遵从几何运算法则。这样的量叫“物理矢量”。如速度、加速度、位移、力、冲量、动量、电场强度、磁场强度……等都是矢量。可用黑体字(例如F)或带箭头的字母(例如 ![]() )来表示矢量。
)来表示矢量。
【矢量的合成】即矢量相加。矢量之间的运算要遵循特殊法则。矢量加法一般用平行四边形法则。可推广至三角形法则、多边形法则或正交分解法等。合成的矢量称为矢量和或合矢量。例如,共点力的合成、速度的合成、加速度的合成、位移的合成等等。两个以上矢量相加,可先求出其中两个矢量的合矢量,然后将该合矢量与第三个矢量相加,若求多个矢量的合矢量,可按上述方式类推。另一种简便方法,是将这些矢量的箭尾与箭头依次相连接,然后将第一个矢量的箭尾连到最末一个矢量的箭头的矢量,就是所要求的合矢量。这种矢量合成法叫多边形法。其大小和方向与相加次序无关。矢量减法是矢量加法的逆运算,一个矢量减去另一个矢量,等于加上那个矢量的负矢量。
![]()
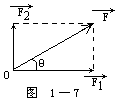
【矢量的分解】它是矢量合成的逆运算,也遵从几何运算法则。若无其它限制,同一个矢量可分解为无数对大小、方向不同的分矢量。因此,把一个矢量分解为两个分矢量时,应根据具体情况,考虑分矢量产生的效果来分解。一般情况下,常将一个矢量 ![]() 分解为互相垂直的两个分矢量
分解为互相垂直的两个分矢量 ![]() 和
和 ![]() 。如图1-7所示,则
。如图1-7所示,则 ![]() =Fcosθ;
=Fcosθ; ![]() =Fsinθ。物理学中常用的有:力的分解、速度的分解、位移的分解、加速度的分解等等。
=Fsinθ。物理学中常用的有:力的分解、速度的分解、位移的分解、加速度的分解等等。
【标量】亦称“无向量”。有些物理量,只具有数值大小,而没有方向。这些量之间的运算遵循一般的代数法则。这样的量叫做“标量”。如质量、密度、温度、功、能量、路程、速率、体积、时间、热量、电阻等物理量。无论选取什么坐标系,标量的数值恒保持不变。矢量和标量的乘积仍为矢量。矢量和矢量的乘积,可构成新的标量,也可构成新的矢量,构成标量的乘积叫标积;构成矢量的乘积叫矢积。如功、功率等的计算是采用两个矢量的标积。A=F·S,P=F·v。力矩、洛仑兹力等的计算是采用两个矢量的矢积。M=r×F,F=qv+B。
【平衡】指物体或系统的一种状态。处于平衡状态的物体或系统,除非受到外界的影响,它本身不能有任何自发的变化。在不同的科学领域,它有不同的涵义。
在力学系统里,平衡是指惯性参照系内,物体受到几个力的作用,仍保持静止状态,或匀速直线运动状态,或绕轴匀速转动的状态,叫做物体处于平衡状态,简称物体的“平衡”。因稳度的不同,物体的平衡分为:稳定平衡、随遇平衡、不稳定平衡三种情况。
【物体的平衡条件】要使物体保持平衡状态,作用在物体上的力或力矩必须满足一定的条件,这叫做“物体平衡条件”。使物体保持平衡的条件是:(1)使物体处于平动平衡的条件是,作用在物体上的合外力为零,即Σ ![]() =0;(2)使物体处于转动平衡的条件是,作用在物体上的所有力的合力矩为零,即Σ
=0;(2)使物体处于转动平衡的条件是,作用在物体上的所有力的合力矩为零,即Σ ![]() =0。当上述两个条件同时满足时,物体处于完全的平衡。中学阶段只讨论平面力系的平衡条件。处于平衡状态的物体,可以是静态平衡,即物体既无平动又无转动,保持静止状态;也可以是动态平衡,即物体作匀速直线运动或匀角速转动。无论物体处于静态平衡还是动态平衡,物体受力状况并无区别,区别在于物体的初始运动状态,即物体开始处于力平衡的即时,它是静止的还是作平动或转动。处于平衡状态的物体,由于某种外界微小的作用而偏离了平衡状态时,可能有四种情形。见平衡状态条。
=0。当上述两个条件同时满足时,物体处于完全的平衡。中学阶段只讨论平面力系的平衡条件。处于平衡状态的物体,可以是静态平衡,即物体既无平动又无转动,保持静止状态;也可以是动态平衡,即物体作匀速直线运动或匀角速转动。无论物体处于静态平衡还是动态平衡,物体受力状况并无区别,区别在于物体的初始运动状态,即物体开始处于力平衡的即时,它是静止的还是作平动或转动。处于平衡状态的物体,由于某种外界微小的作用而偏离了平衡状态时,可能有四种情形。见平衡状态条。
【平衡状态】处于平衡状态的物体,由于外界某种微小的作用而偏离了平衡状态时,因稳度的不同,物体的平衡状态可分为四种情形:稳定平衡;不稳定平衡;亚稳平衡;随遇平衡。这些平衡状态的区分,应视我们放置该物体的平衡位置而定。
1.稳定平衡:凡能在被移动离开它的平衡位置后,仍试图回复其原来位置(此时其重心比较低)从而恢复到原来的平衡状态的物体,它原来的平衡状态叫“稳定平衡”。例如,圆球体在一个凹进的圆盘中时;一圆锥体以其底面竖立时,都属于稳定平衡状态。
2.不稳定平衡:处于平衡状态的物体,由于受到某种外界微小的作用,如果物体稍有偏离就不能恢复到原来的平衡状态,这种情况叫“不稳定平衡”。例如,当一个圆球体放在一个凸起的圆盘上,或是一个圆锥体,以其尖端竖立在一个平面上,这些物体都处于不稳定平衡状态。翻倒后,一直要等到它们的重心相对地取得最低位置时,这些物体才会静止不动。即任何微小的运动都能使其重心降低的物体,一定处于不稳定平衡状态之下。
3.亚稳平衡:如果物体在外力作用下,稍有偏离尚可恢复,而偏离稍大就失掉平衡的状态,称为“亚稳平衡”。
4.随遇平衡:如果物体在外界作用下,它的平衡状态不随时间和坐标的变化而改变,这种状态叫“随遇平衡”。例如,当一个圆球体停在一个水平平面上的时候,或是一个圆锥体以其外壳的一条边线与平面相接触,即横向放在一个水平平面上时,都会出现随遇平衡状态。这些物体如被移置到一个新的位置时,虽然它们不能自动地恢复其原来的位置,但它们在新的位置上,却仍能停住不动,其重心之高度,亦保持不变。一般说来,任何微小之运动,既不能将其重心提高,亦不能使其重心降低之物体,一定处于随遇平衡状态之下。
上述几种平衡状态,是处于重力场以及其他有势场的物体在场作用下的平衡情况。处于有势场的物体和场一起具有势能,而物体都有向势能较小位置运动的趋势。稳定平衡是指物体处于势能最小位置,当稍有微小扰动,令其离开平衡位置,外界必须对它作功,势能增加,在扰动后物体将自动回到原来势能最小的位置。所谓不稳定平衡是指物体处于势能最大时的平衡。任何微小的扰动即能引起重力对它作功,势能继续减小,不能再自动恢复原状。而随遇平衡的物体,受到扰动,势能将保持不变,在任意位置可继续保持平衡。在日常生活中对具体问题应具体分析,例如,放在桌上的鸡蛋,对旋转运动来说,是处于随遇平衡状态下;对倾倒运动而言,开始是不稳定平衡,接着则为稳定平衡。
【二力的平衡】对一个物体施加两个力,而这两个力同时作用在一条直线上,其力的大小相等方向相反,此物体运动状态不发生任何变化。这时二力的作用互相抵消,这就是二力的平衡。
【力学平衡】物体相对于惯性系处于静止或匀速直线运动的状态。
【平衡力】平衡力系中的任一力称为该力系中其余力的平衡力。
【平衡力系】作用于刚体并使它保持力学平衡状态的力系,谓之平衡力系。一个力系为平衡力系的必要且充分条件其一是:力系中各力的矢量和为零,即该力系的主矢为零。其二是:力系中各力对任一点力矩的矢量和为零,即该力系对任一点的主矩为零。
【受力分析】解力学题,重要的一环就是对物体进行正确的受力分析。由于各物体间的作用是交互的,任何一个力学问题都不可能只涉及一个物体,力是不能离开物体而独立存在的。所以在解题时,应根据题目的要求,画一简图,运用“隔离法”,进行受力分析。由于物质分为实体与场,所以,力的作用方式也分为两类,一类是实物对研究对象的作用,其特点是施力物与研究对象直接接触(如摩擦力、空气阻力、弹性力等);另一类是物体通过它所激发的场对研究对象的作用,其特点是激发场的物体与研究对象不直接接触(如重力、静电力等)。在力学中,以场方式作用于研究对象的力经常是重力。由此,得出进行受力分析的规则:在研究物体受哪些力时,除重力外,就只看该物体与之相触的物体,凡与研究对象接触的物体对研究对象都可能有力作用。
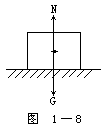
1.水平面上的物体一木块静置于桌面上,木块受两个力作用。一是受地球的吸引而受到重力G,方向竖直向下;另一个是木块压在桌面使桌面发生极微小的形变,桌面对木块产生支持力N,方向竖直向上。如图1-8所示,因木块是静止的,所以G和N是作用在木块上的相互平衡的力,它们大小相等方向相反。
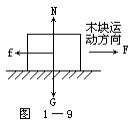
在水平面上运动的木块,除受重力G和支持力N的作用外,还受到滑动摩擦力f的作用。滑动摩擦力f的方向与木块运动方向相反。木块受力图如图1-9所示。木块受空气阻力的方向跟木块运动方向相反。空气阻力的大小踉物体的运动速度,以及物体的横截面大小有关。如果用水平的绳拉木块前进,木块除受重力G,支持力N和滑动摩擦力f的作用外,还受到绳的拉力F,木块共受四个力,如图1-10所示。

2.在斜面上运动的物体:如图1-11所示,一木块沿斜面下滑,木块受到竖直向下的重力G。木块压斜面,斜面发生形变而对木块产生支持力N,方向垂直于斜面并指向被支持的木块。木块还受到与其运动方向相反,沿斜面向上的滑动摩擦力f。重力沿斜面的分力使物体沿斜面加速下滑而不存在一个独立于重力之外的所谓“下滑力”。

3.一轻绳通过定滑轮,用一水平力F拉物体A使之向右运动,B落于A上,其间的摩擦系数为μ1,A与桌面间摩擦系数为μ2,不计空气阻力,分析A、B所受的力。如图1-12所示。
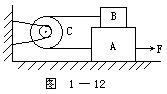
先研究物体A。如图1-13所示。A受地球吸引力 ![]() (向下),与A接触的有人、物体B、绳、桌面、空气。分析得:人对A的拉力
(向下),与A接触的有人、物体B、绳、桌面、空气。分析得:人对A的拉力 ![]() (向右),B对A的正压力
(向右),B对A的正压力 ![]() (向下),B给A的摩擦力
(向下),B给A的摩擦力 ![]() (向左),绳的拉力
(向左),绳的拉力 ![]() (向左),桌面对A的正压力
(向左),桌面对A的正压力 ![]() (向上,也叫支持力),桌面施于A的摩擦力
(向上,也叫支持力),桌面施于A的摩擦力 ![]() (向左)。其次,以物体B为研究对象。如图1-14所示。B受地球的引力
(向左)。其次,以物体B为研究对象。如图1-14所示。B受地球的引力 ![]() (向下),与B接触的有物体A、绳和空气。A对B的正压力
(向下),与B接触的有物体A、绳和空气。A对B的正压力 ![]() (向上),A对B的摩擦力
(向上),A对B的摩擦力 ![]() (向右),绳子的拉力
(向右),绳子的拉力 ![]() (向左)。
(向左)。

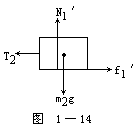
注意: ![]() 与
与 ![]() 是一对作用力和反作用力。
是一对作用力和反作用力。 ![]() 与
与 ![]() 是一对作用力和反作用力。而f1=μ1N1,f2=μ2N2。
是一对作用力和反作用力。而f1=μ1N1,f2=μ2N2。
在教学中应该注意,尽管物体静止在水平地面上时,重物对地面的压力与物体的重力在数值上相等,但在某些场合下,压力并不等于重力。产生重力作用不一定要两物接触,而压力则必须要两物接触才能产生。还应讲明的是,物体对斜面的压力就不等于物体的重力。当斜面上的物体下滑时,重力G分解为沿斜面平行的分力F1和沿斜面垂直的分力F2。F1可称为下滑力,F2称为正压力。
【三力平衡条件】任意两个力的合力与第三个力大小相等方向相反,且在一条直线上。故三个力平衡时,必在同一平面内,且作用线必交于一点,此即刚体受三个力作用而平衡的条件。
【质点】不考虑物体本身的形状和大小,并把质量看作集中在一点时,就将这种物体看成“质点”。研究问题时用质点代替物体,可不考虑物体上各点之间运动状态的差别。它是力学中经过科学抽象得到的概念,是一个理想模型。可看成质点的物体往往并不很小,因此不能把它和微观粒子如电子等混同起来。若研究的问题不涉及转动或物体的大小跟问题中所涉及到的距离相比较很微小时,即可将这个实际的物体抽象为质点。例如,在研究地球公转时,地球半径比日、地间的距离小得多,就可把地球看作质点,但研究地球自转时就不能把它当成质点。又如物体在平动时,内部各处的运动情况都相同,就可把它看成质点。所以物体是否被视为质点,完全决定于所研究问题的性质。
【刚体】在任何力的作用下,体积和形状都不发生改变的物体叫做“刚体”。它是力学中的一个科学抽象概念,即理想模型。事实上任何物体受到外力,不可能不改变形状。实际物体都不是真正的刚体。若物体本身的变化不影响整个运动过程,为使被研究的问题简化,可将该物体当作刚体来处理而忽略物体的体积和形状,这样所得结果仍与实际情况相当符合。例如,物理天平的横梁处于平衡状态,横梁在力的作用下产生的形变很小,各力矩的大小都几乎不变。对于形变,实际是存在的,但可不予考虑。为此在研究天平横梁平衡的问题时,可将横梁当作刚体。
【机械运动】物体之间或同一物体各部分之间相对位置随时间的变化叫做机械运动。它是物质的各种运动形态中最简单,最普遍的一种。例如,地球的转动、弹簧的伸长和压缩等都是机械运动。而其他较复杂的运动形式,例如,热运动、化学运动、电磁运动、生命现象中都含有位置的变化,但不能把它们简单地归结为机械运动。
【参照系】又称“参考系”,“参照物”。为了确定物体的位置和描述物体的运动而被选作参考的物体或物体系。如果物体相对于参照系的位置在变化,则表明物体相对于该参照系在运动;如果物体相对于参照系的位置不变,则表明物体相对于该参照系是静止的。同一物体相对于不同的参照系,运动状态可以不同。在运动学中,参照系的选择可以是任意的。研究和描述物体运动,只有在选定参照系后才能进行。如何选择参照系,必须从具体情况来考虑。例如,一个星际火箭在刚发射时,主要研究它相对于地面的运动,所以把地球选作参照物。但是,当火箭进入绕太阳运行的轨道时,为研究方便,便将太阳选作参照系。为研究物体在地面上的运动,选地球作参照系最方便,例如,观察坐在飞机里的乘客,若以飞机为参照系来看,乘客是静止的;如以地面为参照系来看,乘客是在运动。因此,选择参照系是研究问题的关键之一。
【坐标系】为了说明质点的位置,运动的快慢、方向等,必须选取坐标系。在参照系中,为确定空间一点的位置,按规定方法选取的有次序的一组数,叫做“坐标”。在某一问题中规定坐标的方法,就是该问题所用的坐标系。坐标系的种类很多,常用的坐标系有:笛卡儿直角坐标系、平面极坐标系、柱面坐标系和球面坐标系等。中学物理学中常用的坐标系,为直角坐标系,或称为正交坐标系。
【平动】也称平移,平行移动。是机械运动的一种特殊形式,是刚体的一种最基本的运动。运动物体上任意两点所连成的直线,在整个运动过程中,始终保持平行,这种运动叫做“平动”。在同一时刻,运动物体上各点的速度和加速度都相同。因此在研究物体的平动时,可不考虑物体的大小和形状,而把它作为质点来处理。
【转动】机械运动的一种最基本的形式。运动物体上,除转动轴上各点外,其他各点都绕同一转动轴线作大小不同的圆周运动,这种运动叫做“转动”。物体上各点的运动轨迹是以转轴为中心的同心圆。在同一时刻,转动物体上各点的线速度和线加速度不尽相同。距转轴较近的点,其线速度和线加速度都较小,但角速度和角加速度都相同。当刚体绕一固定轴线转动时,称为“定轴转动”,如门、窗、机器上飞轮的运动等。当刚体绕一固定点转动时,称为“定点转动”,如回转仪的转子的运动等。有时,当一点以另一固定点为中心作圆周运动时,也称为“该点绕中心点的转动”,如行星绕恒星的运动。电子绕原子核的运动等。
【位置】指物体某一时刻在空间的所在处。物体沿一条直线运动时,可取这一直线作为坐标轴,在轴上任意取一原点O,物体所处的位置由它的位置坐标(即一个带有正负号的数值)确定。
【位移】质点从空间的一个位置运动到另一个位置,它的位置变化叫做质点在这一运动过程中的位移。它是一个有大小和方向的物理量。位移是矢量。物体在某一段时间内,如果由初位置移到末位置,则由初位置到末位置的有向线段叫做位移。它的大小是运动物体初位置到末位置的直线距离;方向是从初位置指向末位置。位移只与物体运动的始末位置有关,而与运动的轨迹无关。如果质点在运动过程中经过一段时间后回到原处,那么,路程不为零而位移则为零。在国际单位制中,位移的单位为:米。此外还有:厘米、千米等。
【路程】质点从空间的一个位置运动到另一个位置,运动轨迹的长度叫做质点在这一运动过程所通过的路程。路程是标量,即没有方向的量。位移与路程是两个不同的物理量。在直线运动中,路程是直线轨迹的长度;在曲线运动中,路程是曲线轨迹的长度。当物体在运动过程中经过一段时间后回到原处,路程不为零,位移则等于零。
【运动】在力学中所讲的运动指的是机械运动。物质的质点或质点组与参照系之间的位置随时间而改变的过程叫机械运动。同一物体的运动以不同参照系看来并不相同。乘车的旅客,以车厢作参照系是静止的,而以地面作参照系则是运动的。因此在具体描述物体的运动时必须先选定一个参照系,通常都以地球作为参照系。有时在一个力学问题中同时采用几个参照系时,把相对于非基本参照系的运动称为相对运动。
【时间】量度两个时刻之间的间隔长短的物理量叫做“时间”。它表征物质运动过程的持续性和顺序性。任何一种周期运动的周期都可作为时间标准,如中国古代的水漏,十二地支(子,丑,寅,卯……)都是利用周期性的计时方法。时间是物理学中的一个基本物理量。一段时间在时间坐标轴上用一线段表示。为了用具体数字说明时间,必须选择某一时刻作为计时起点,这是人为的。计时起点不一定是物体开始运动的时刻。在物理学中,将太阳每连续两次经过观察者所在的子午线的时间称为一个太阳日,即一昼夜。因太阳日略有差异,取一年中所有太阳日的平均值作为时间的标准,称为一个平均太阳日,简称1日。1日分为24小时,1小时分为60分,1分又分为60秒,于是规定1日的86400分之一为1秒作为时间标准。但是这样规定的秒是不精确的。1967年在第13届国际计量大会上,规定以基态铯133原子的两超精细结构能级之间的辐射周期的9192631770倍为1标准秒。时间常跟位移或平均速度相对应,例如:“五秒钟内所发生的位移”或“头两秒内的平均速度”。
【时刻】把短暂到几乎接近于零的时间叫即时,即时表示时刻。时刻与时间不同。例如,事件发生在什么时刻?事件持续了多长时间?这是两个不同的概念,应区别前几秒末后几秒初、第几秒末、第几秒初等等时刻的概念,和前几秒后几秒、几秒内、第几秒等等时间的慨念。用一根无限长的只表示先后次序不表示方向的带箭头的线来描述时间和时刻,这条带箭头的线叫做时间轴。时间轴上的每一个点表示一个时刻。时刻是衡量一切物质运动先后顺序,它没有长短,只有先后,它是一个序数。时间轴上相应两个时刻之间的间隔长短,表示一段时间,时间是一个只有长短,而没有方向的物理量。时间具有连续性、单向性、序列性,并且总是不断向前流逝。
【速度】描述物体运动的方向和位置变化快慢的物理量。它是矢量。速度的量值表示位置变化的快慢,它的方向是位移的方向。在国际单位制中,速度的单位是:米/秒。此外还有厘米/秒、千米/时。
【匀速度】即匀速直线运动的速度。物体作匀速直线运动时的速度叫做“匀速度”。所以匀速度的量值是以运动物体所通过的路程(S)和通过这段路程所需的时间(t)的比值来量度,设v表示匀速度,则其数学表达式为
![]()
【匀变速直线运动的速度】当物体做匀速运动时,在相等的时间里发生的位移都相等。若已知位移和时间的比值,即知道了速度,就可以确定位移和时间的关系;如已知初位置,就可以知道任一时刻的位置。在匀变速运动中,在相等的时间里速度的变化都相等,若知道速度的变化和时间的比值,即知道了加速度,就可以确定速度的变化和时间的关系;如果还知道初速度,就可以知道任一时刻的速度。将匀变速运动的
![]()
Ut=v0+at
这一公式表示出匀变速运动的即时速度是如何随着时间而变化的。根据这个公式,如果已经知道做匀变速运动的物体的初速度和加速度,就可以求出物体在任一时刻的即时速度。如果匀变速运动的初速度为零,即v0=0,上式就可简化成下式:vt=at。当物体受到一个与V0同方向或反方向的恒力的作用时,或者物体受到几个力的作用,这些力的合力的方向与V0的方向相同或相反,合力的大小保持不变时,物体就做匀变速直线运动。
【平均速度】平均速度是描述作变速运动物体之位置改变的平均快慢程度的物理量,是以作变速运动的物体所通过的路程(S)跟通过这段路程所需的时间(t)的比值来量度,即
![]()
![]()
在不同段路程上的平均速度 ![]() 是不同的,在应用
是不同的,在应用 ![]() 时应明确是哪一段路程上的
时应明确是哪一段路程上的 ![]() 。因此,在某段路程的
。因此,在某段路程的 ![]() 只能用于该段路程的计算上。同样,在不同时间间隔的平均速度也各不相同,必须指明在哪一段时间间隔内,
只能用于该段路程的计算上。同样,在不同时间间隔的平均速度也各不相同,必须指明在哪一段时间间隔内, ![]() 就只能应用在所指定的时间间隔的有关问题上。由于物体在作变速直线运动时,它在选取的一段时间间隔内,运动的快慢程度也是在不断变化着的,所以平均速度不是运动物体的真实速度,它只能粗略地描述变
就只能应用在所指定的时间间隔的有关问题上。由于物体在作变速直线运动时,它在选取的一段时间间隔内,运动的快慢程度也是在不断变化着的,所以平均速度不是运动物体的真实速度,它只能粗略地描述变
![]()
【即时速度】即时速度是指运动物体在某一时刻或通过路程上某一位置时的速度,也叫“瞬时速度”。即时速度是力学中的一个重要概念,学生难于理解,而教师讲授也感困难,因此对此概念必须有清晰的认识。“即时”是时间不断流逝中的一刹,它不能脱离一段时间。因此即时速度与一段时间的平均速度有联系。要研究t时刻的即时速度,首先研究一下t附近,在t→t+△t时间间隔内的平均速度 ![]() 。若△t越短,物体的运动快慢在这段时间△t内的变化也就越小,计算所得的平均速度就越能精细地描写物体在该时刻t附近的运动快慢。因此,运动物体在某一时刻的即时速度就等于在这一时刻前后某一趋近于零的时间间隔内的平均速度的极限。即时速度能准确地表示变速运动中各个时刻的运动情况。汽车上的速度计就是测量汽车即时速度的仪器,由于本身结构和机件的惯性,读数也只是近似的。初速度、某秒末的速度、线速度等都是指即时速度。变速运动每一时刻的即时速度都不同。因此谈到即时速度必须指出是哪一时刻或哪一位置的即时速度。而在匀速运动中,每一时刻的即时速度不变。
。若△t越短,物体的运动快慢在这段时间△t内的变化也就越小,计算所得的平均速度就越能精细地描写物体在该时刻t附近的运动快慢。因此,运动物体在某一时刻的即时速度就等于在这一时刻前后某一趋近于零的时间间隔内的平均速度的极限。即时速度能准确地表示变速运动中各个时刻的运动情况。汽车上的速度计就是测量汽车即时速度的仪器,由于本身结构和机件的惯性,读数也只是近似的。初速度、某秒末的速度、线速度等都是指即时速度。变速运动每一时刻的即时速度都不同。因此谈到即时速度必须指出是哪一时刻或哪一位置的即时速度。而在匀速运动中,每一时刻的即时速度不变。
必须注意:“即时速度就是很短时间内的平均速度”这句话是错误的。因为很短时间,总是指一段有限的确定时间,它与“趋近于零”的概念是不同的,与即时速度定义中的要求不符。变速运动的即时速度,描述物体在某时刻运动的快慢和运动的方向。一般说,物体在不同时刻具有不同的即时速度,它随时间而变。变速直线运动(指沿一个方向的),速度的方向不变,而速度大小随时间变化;曲线运动,速度的大小和速度的方向皆可变化。所以,严格来讲速度与速度的大小是有区别的,前者是矢量,包含大小和方向两方面的涵义;后者仅指数值而无方向,往往称之为速率。不能理解即时速度的大小为“单位时间内通过的路程”。
【速率】描述物体运动快慢,而不表示运动的方向,是一个标量。速率有时表示物体单位时间所走的路程。在国际单位制中它的单位是米/秒,此外还有:厘米/秒、千米/时。
【平均速率】质点运动的路程△S与相应的时间△t的比,称为运动质点在时间△t内的平均速率,常用符号 ![]() 表示。即
表示。即
![]()
【瞬时速率】当时间△t趋于零时,质点运动的平均速率的极限值称为质点在时刻t的瞬时速率,又称质点在时刻t的即时速率,简称质点在时刻t的速率,常用符号v表示。即
![]()
【加速度】描述运动物体的速度变化快慢程度的物理量。它是矢量,用 ![]() 表示。它的合成与分解遵从平行四边形法则。加速度是以速度的变化量跟发生这种变化所经过的时间的比值为量度。物体在作直线运动时,如果在某一时刻t0的速度是V0(初速度),到时刻t的速度变为vt(末速度),那么vt-v0就称为在t-t0这段时间内的速度变化量,用a代表加速度,其表达式为
表示。它的合成与分解遵从平行四边形法则。加速度是以速度的变化量跟发生这种变化所经过的时间的比值为量度。物体在作直线运动时,如果在某一时刻t0的速度是V0(初速度),到时刻t的速度变为vt(末速度),那么vt-v0就称为在t-t0这段时间内的速度变化量,用a代表加速度,其表达式为
![]()
如果t0=0,则上式可写成
![]()
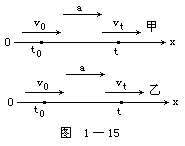
其国际单位制单位为米/秒2,常用的还有厘米/秒2等。加速度的产生是由于物体受外力的作用,它的方向和运动物体所受合外力的方向一致。但它和运动的方向不一定相同。在直线运动中,加速度的方向总是沿一直线,因此可用正、负号来表示它的方向。由加速度公式知:当a为正值时,vt>v0,表示速度在不断增加,物体作加速运动,如图1-15甲所示,加速度a的方向是沿着坐标OX的正方向;当a为负值时,vt<v0,表示速度在不断减少,物体作减速运动,如图1-15乙所示,加速度a的方向是沿着XO方向(即OX的反方向)。在变速运动中速度小时加速度不一定小;速度大时加速度不一定大。例如,当火车从车站驶出时,虽然速度不大,但速度变化较大;当火车高速行驶时,在平直轨道上保持匀速前进,行车速度很大,但是速度却无变化,加速度为零。因此说,在加速运动中,加速度取正值,叫正加速度;在减速运动中,加速度取负值,叫负加速度。
【匀加速度】在匀变速运动中,速度的变化量跟发生这种变化所经过的时间的比是一个恒量,用a代表这段时间内运动物体的加速度,则
![]()
具有这种性质的加速度叫做匀加速度,或称匀变速直线运动的加速度。在匀速运动中Vt-v0=0,所以a=0,即没有加速度。在匀变速运动中,a是一个恒量。应注意的是,在各种不同的匀变速直线运动中,相等时间内速度的变化量不同,因此加速度也不同,上式的恒量也不会是相同的。
【平均加速度】质点速度改变的平均快慢程度,称为“平均加速度”。它是描述作变速直线运动物体之速度的方向和速度大小改变的快慢程度的物理量。其数学表达式为:
![]()
物体作一般变速运动时,平均加速度也因所取时间的不同而有差别,所以在讲平均加速度时,一定要指出是哪一段时间内的平均加速度。平均加速度只能表明某一段路程中(或某一段时间内)速度改变快慢程度的近似情况,在这段路程中,各个分段中的加速度,跟全段路程中的平均加速度可能有所不同。所以,平均加速度不是物体运动的真实加速度。
【即时加速度】亦称“瞬时加速度”。是指运动物体在某一时刻或通过路程上某一位置时的加速度,谓之“即时加速度”。平均加速度是以速度的变化量和发生这种变化所经过的时间的比值来量度的,如果我们选取的时间间隔极短,即t至t+△t时间内, ![]()
![]()
动的物体在某瞬间的即时速度可能为零,但经过时间间隔△t,其速度
![]()
不一定等于零。例如,竖直上抛的物体在到达最高点的瞬间,即时速度是等于零的,但其加速度仍为竖直向下的重力加速度,其值为9.8米/秒2。
【重力加速度】在地球表面上方不太高的范围内,质点因受地球引力作用而产生的加速度,称为“重力加速度”。也可以说:物体由于重力作用而获得的加速度叫做“重力加速度”。地面附近的物体,由于其他天体距离它很远,地球上其他物体对它的万有引力很小,所以该物体的重力皆指地球对它的万有引力,其方向指向地心。在地面附近,任何物体的重力加速度在同一地点都相同,但在不同地点,物体的重力加速度稍有不同。这种加速度用字母g表示。经测定,在赤道附近,g=9.78米/秒2;在地球北极g=9.83米/秒2;在北京g=9.80米/秒2;在上海g=9.79米/秒2。在一般要求不须太精确的计算中,可近似地取g=9.8米/秒2。竖直上抛物体的运动是一种匀减速直线运动,在运动过程中只受到重力作用(空气阻力忽略不计),这时它的加速度也就是重力加速度。但是加速度的方向和物体开始竖直上抛时的初速度方向相反。如果取运动物体竖直向上的方向为正,则加速度的方向应取负值,即a=-g=-9.8米/秒2。以上各地的重力加速度,都是就平均海平面处而言。在离地面极高处,重力加速度就显著减小。又因地球是椭圆球,其极半径比赤道半径约小0.3%,所以同一物体在不同的地域所受重力略有不同。地面附近的物体随地球一起转动,万有引力还必须提供其向心力,所以同一物体在不同的地域所受的重力不仅数值略有不同,而且方向也并不指向地心。因此在不同地域的重力加速度也略有不同,方向也并不指向地心。世界主要地区的重力加速度数值见附表。
【图象表示法】亦称“坐标图解法”。利用平面坐标来表明两个物理量的函数关系,它能形象地描述机械运动的基本规律以及其他很多的规律。例如,机器的性能、晶体管的特性曲线、物质的物理性质及物质的热运动等。通过坐标图上的函数图线,可以直接读出待求量的大小,或用一些简单的计算,将要求的量找出来。图象中的纵、横两坐标轴上的标度,代表互为函数关系的两个不同的物理量。常用的有:V-t图象、P-V图象、S-t图象、P-T图象、V-T图象、振动图象、波动图象、温度—时间(T)—(t)图象、伏安图象等。
【位移—时间图象】简称“位移图象”,它是用图象表示物体位移和时间的关系。匀速直线运动的位移S是时间t的正比函数S=Vt。在物体的直线运动中以横轴表示运动物体运动的时间t,纵轴表示物体运动的位移S。S-t图象的用途有:已知S求相应的时间t;已知t求相应的位移S;还可从直线的斜率的数值得出速度的大小,在同一坐标平面上,斜率越大,则直线越陡,表示速度越大,故可由图线求速度。
【速度—时间图象】简称“速度图象”。它是用图象表示匀速直线运动的速度和时间的关系。当物体作直线运动时,在平面直角坐标系中,用横轴表示时间,纵轴表示物体运动的速度。借助速度—时间图线可以找到运动物体在任何时刻的即时速度。它的用途较多,例如,已知时刻t可求相应的速度vt;已知即时速度vt,可求相应的时刻t;图象斜率的大小表示加速度的大小,斜率的正负表示加速度的方向,故可由图线求加速度;用速度图象求质点在任何时间内的位移,位移的数值相当于速度图象曲线下的“面积”的数值。这个“面积”的单位是(米/秒)×秒=米,而不是米2;可在同一坐标上比较几个物体的运动状况;并可判断某一运动过程的几个阶段的运动性质与状况。
【直线运动】质点在一条确定直线上的运动,称为“直线运动”。质点的位置,以离原点的距离,用坐标X表示。它是研究复杂运动的基础,按其受力的不同可分:匀速直线运动;匀变速直线运动(包括匀加速或匀减速直线运动,以及自由落体,竖直上、下抛运动);变速直线运动。
【匀速直线运动】物体沿一直线运动且在任何相等的时间里位移都相等。或者说速度的大小和方向都不改变的运动,谓之“匀速直线运动”。它的特征是:它的速度是一个恒量,即任一时刻速度(v)都相同。它
![]()
过的时间。产生匀速直线运动的条件是:当运动物体所受外力的合力等于零时,物体做匀速直线运动。所以,真正的匀速直线运动实际上是很难出现的。为简化问题,不妨碍结果的准确性,而把近似的匀速直线运动当作真正的匀速直线运动来处理。
【变速运动】亦称“非匀速运动”。物体的速度随时间而变化,可能是快慢程度,也可能是运动方向发生变化,还可能是快慢和方向同时都发生改变。它是最常见的一种机械运动。按其运动的轨迹来分有直线运动和曲线运动。例如,火车、汽车和轮船从车站或码头开出的运动。又如转弯的车辆和钟的摆锤的摆动等。在中学阶段,一般是讨论匀变速直线运动、抛体运动和匀速圆周运动。
【速直线运动】在相等的时间里,位移并不都是相等的直线运动。它是物体运动最常见的形式之一。由于物体运动的快慢经常改变,所以常用平均速度和即时速度这两个物理量来描述物体运动的快慢程度。
【匀变速直线运动】加速度的大小和方向保持不变的直线运动。匀变速直线运动的基本特点是:在任何相等的时间内其速度的增量相等。质点在作匀变速直线运动时,其速度图线v—t图是一条倾斜的直线,而直线的斜率就等于其加速度的大小。即
![]()
式中v0、vt依次为作匀变速直线运动的初速度和末速度。它的运动规律可通过几个公式反映出来:速度(vt)与时间(t)的关系是vt=v0
![]()
![]()
叫匀加速直线运动;当加速度是一个负恒量时,物体的运动叫匀减速直线运动。当物体受到一个与V0。同方向或反方向的恒力的作用时,或者物体受到几个力的作用,这些力的合力的方向与v0的方向相同或相反,合力的大小保持不变时,物体就做匀变速直线运动。
【匀变速直线运动的基本公式】匀变速直线运动的规律可以通过下列公式反映出来,即
速度公式vt=v0+at
![]()
速度路程公式vt2=v02+2aS
公式中共有v0、vt、S、a、t五个物理量,除t之外,其余四个都是矢量,但必须注意它们的方向。由于物体是作直线运动,故只须用正、负号即可表示它们的方向。通常规定初速度v0的方向为正方向。当加速度a与v0反向时,a为负,物体作减速运动。速度路程公式是由速度公式和路程公式联立消去t以后得到的。可见,上述三个公式中只有两个独立,在v0、vt、a、S、t这五个量中必须给出三个,才能通过公式找出另外两个来。
【自由落体】不受任何阻力,只在重力作用下而降落的物体,叫“自由落体”。如在地球引力作用下由静止状态开始下落的物体。地球表面附近的上空可看作是恒定的重力场。如不考虑大气阻力,在该区域内的自由落体运动是匀加速直线运动。其加速度恒等于重力加速度g。虽然地球的引力和物体到地球中心距离的平方成反比,但地球的半径远大于自由落体所经过的路程,所以引力在地面附近可看作是不变的,自由落体的加速度即是一个不变的常量。它是初速为零的匀加速直线运动。
自由落体运动的特点,体现在“自由”二字上,其含意为:物体开始下落时是静止的即v0=0。如果给物体一个初速度竖直下落,不能算自由落体。物体在下落过程中,除受重力作用外,不再受其他任何作用力(包括空气阻力)。以v0=0,a=g代入匀变速直线运动的三个公式,可以得到关于自由落体运动的三个公式:
![]()
通常在空气中,随着自由落体运动速度的增加,空气对落体的阻力也逐渐增加。当物体受到的重力等于它所受到的阻力时,落体将匀速降落,此时它所达到的最高速度称为终端速度。例如伞兵从飞机上跳下时,若不张伞其终端速度约为50米/秒,张伞时的终端速度约为6米/秒。
【自由落体运动】见“自由落体”。
【抛体】凡同时参与匀速运动和自由落体运动的物体都叫“抛体”。在重力作用下,具有初速度v0的物体所做的运动,谓之“抛体运动”。抛体在运动过程中,恒力跟速度的夹角是变化的。当匀速运动的初速度v0和自由落体的加速度g方向相同时,物体作下抛运动;方向相反时作上抛运动。物体作下抛或上抛运动的位移公式是
![]()
当抛体的初速度与重力加速度的方向有一夹角时,物体作斜抛运动;方向垂直时物体作平抛运动,平抛和斜抛运动可根据运动的叠加原理,将其分解为竖直方向的加速运动与水平方向的匀速运动而分别予以讨论。当空气阻力可略去不计时,任何一种轨迹是曲线的抛体运动,都可以看成是由水平方向上的匀速直线运动和竖直方向上的匀变速直线运动所组成的合运动。因此匀速直线运动和匀变速直线运动的规律,以及运动的合成与分解,都是解决抛体运动问题的基础。
【抛体运动】见“抛体”。
【竖直上抛运动】仅受重力作用的质点,以初速v0垂直向上抛出的运动称为垂直上抛运动。上抛运动是初速不为零的匀减速直线运动。它是匀变速运动的一种。可看成竖直向上的初速度为v0的匀速直线运动和竖直向下的自由落体运动的合运动。如果规定v0方向为正方向,则加速度a=-g。任一时刻的合速度vt=v0-gt,经过一段时间t,合
![]()
几点:①物体上升到最高位置时的速度为零,所以它上升到最大高度的
![]()
![]() ④物体经过同一点时速度的量值相等,方向相反。⑤竖直上抛运动公式,不但在物体到达最高位置前一段时间任何时刻适用,而且当到达最高位移又返回原来位置,乃至返回原位置后又继续向下运动时的任何时刻也都适用。当抛体在原处上方,则h为正号,表示h为抛体上升的高度;如果抛体已返回原处继续下落一段距离,则h为负号,表示h为抛体落至原处以下的距离。
④物体经过同一点时速度的量值相等,方向相反。⑤竖直上抛运动公式,不但在物体到达最高位置前一段时间任何时刻适用,而且当到达最高位移又返回原来位置,乃至返回原位置后又继续向下运动时的任何时刻也都适用。当抛体在原处上方,则h为正号,表示h为抛体上升的高度;如果抛体已返回原处继续下落一段距离,则h为负号,表示h为抛体落至原处以下的距离。
在教学中,为取得较好的教学效果,应该强调:①了解物体被抛出后运动的过程。物体以初速度v0,加速度a=-g,竖直向上作匀减速运动,速度逐渐减少,最后为零,这时物体到达最高点。在达到最高点瞬间,物体的即时速度虽然为零,但加速度仍为竖直向下的重力加速度g。物体从最高点自由下落,速度逐渐增加,回到原处,其速度与上抛速度相等,但方向正好相反。物体如果继续下落,则位移成为负值。②搞清用正负号表示矢量的意义。在处理竖直上抛运动中,我们把竖直向上的初速度v0的方向定为正方向,所以加速度a=-g,其负号表示加速度a的方向竖直向下。物体在抛出点以上,位移为正;物体运动到抛出点以下,位移为负。末速度vt为正,表示物体仍然继续在竖直向上运动;vt为负表示速度的方向竖直向下,物体已从最高点竖直下落。按照这样的规定,竖直上抛运动的公式为
![]()
的g=9.8米/秒2,不要再认为g=-9.8米/秒2。③竖直上抛运动与自由落体运动间的二个关系:其一,竖直上抛运动到最高点需要的时间,
![]()
其二,竖直上抛运动对物体的初速度在数值上等于从最高点自由落体回原地的末速度,但是它的方向相反。
【竖直下抛运动】以某一初速,将物体铅直下抛之运动。空气阻力不计时,设抛出时之初速度为 ![]() ,重力加速度为
,重力加速度为 ![]() ,经时间t后,其末速度
,经时间t后,其末速度 ![]() 与所经之位移
与所经之位移 ![]() 分别为
分别为
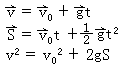
【平抛运动】质点以初速v0沿水平方向抛出后,不计空气阻力,仅受重力作用作曲线运动,这种运动叫“平抛运动”。平抛运动是水平方向的匀速直线运动和铅直方向的自由落体运动的合运动。这两个运动是互相独立的。因此,物体在任何时刻的位置由下列两式确定:
![]()
![]()
确定物体在作平抛运动过程中,它的位移和时间的关系,以及速度跟时间的关系,如图1-16所示。当物体由o点沿水平方向抛出,初速度为v0,y为物体在时间t内竖直下落的距离,x为物体在该时间内水平方向通过的路程。根据运动独立性原理:“物体在一个方向的运动不会因为物体在其他方向的运动而有所改变”。则平抛运动可以分解为以速度为v0的水平方向匀速直线运动和自由落体运动,这两个运动是互相独立的。因此,物体在任何时刻的位置由上述两公式确定。
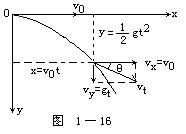
设平抛物体在运动过程中沿水平方向的速度为vx,竖直向下的速度为vy,在任何时刻t的速度为vt,即平抛物体在时刻t的瞬时速度,则从图1-16所示可得:

设vt与水平方向之间的夹角为θ,则
![]()
![]()
![]()
![]()
![]()
【斜抛运动】将物体斜向射出,在重力作用下,物体作曲线运动,它的运动轨迹是抛物线,这种运动叫做“斜抛运动”。根据运动独立性原理,可以把斜抛运动看成是作水平方向的匀速直线运动和竖直上抛运动的合运动来处理。取水平方向和铅直向上的方向为x轴和y轴,则这两个方向的初速度分别是
v0x=v0cosθ,v0y=v0sinθ
t时刻质点分速度是
vx=v0cosθ,vy=v0sinθ-gt
速度是
![]()
t时刻质点的坐标(x,y)是
![]()
从上两式消去t,便得质点运动的轨迹方程
![]()
抛射体所能到达的最大高度为
![]()
其到达最高点所需的时间
![]()
抛射体的最大射程为
![]()
由于空气阻力的影响,物体在空中实际上是沿弹道曲线飞行的,它与抛物线不同,它的升弧和降弧不对称。
【运动迭加原理】亦称“运动的独立性原理”,是物体运动的一个重要特性,是物理学中普遍原理之一。一个物体同时参与几种运动,各分运动都可看作是独立进行的,它们互不影响。而物体的合运动是由物体同时参与的几个互相独立的分运动迭加的结果。例如,初速不为零的匀变速直线运动是由物体同时参与的速度为v0的匀速直线运动,和初速为零的匀变速直线运动迭加的结果。又如,平抛物体运动,由竖直方向的自由落体运动和水平方向的匀速直线运动迭加而成,而这两个运动是彼此独立的。
【曲线运动】物体运动轨迹是曲线的运动,称为“曲线运动”。当物体所受的力和它运动的方向不在同一直线上,物体的运动就是曲线运动。在曲线运动中:当力矢量与速度矢量间的夹角等于90°时,作用力仅改变物体速度的方向,不改变速度的量值;当夹角小于90°时,作用力不仅改变物体运动速度的方向,并且增大速度的量值;当夹角大于90°时,同样改变物体运动速度的方向,但是却减小速度的量值。曲线运动中速度的方向时刻在变,因为是个矢量,既有大小,又有方向。不论速度的大小是否改变,只要速度的方向发生改变,就表示速度矢量发生变化,也就具有了加速度,所以曲线运动是变速运动。常见的曲线运动有:平抛物体运动,斜抛物体运动,匀速圆周运动三种。
【运动的合成】已知物体的几个分运动求其合运动谓之“运动的合成”。由于一个物体常常在同时作几种运动,其中任何一个运动,不影响其它运动。为研究起来方便,将这个物体的整体运动看作是由几个分运动所组成的合运动。运动的合成是指位移的合成,速度的合成或加速度的合成,运动的合成遵从矢量的合成。当物体同时做两个匀速直线运动时,则其合运动也是匀速直线运动。当物体同时一个做匀速直线运动,一个做初速度为零的匀加速直线运动时,若两者在一直线上,则其合运动也是直线运动;若两者不在一直线上,则其合运动是曲线运动。
【运动的分解】已知合运动求各个分运动谓之“运动的分解”。它是研究复杂运动的重要方法。在研究比较复杂的运动时,常常把这个运动看作是两个或几个比较简单的运动组成的,使问题容易得到解决。例如对抛体运动通常利用正交分解法将它看成水平方向的匀速直线运动和竖直方向的匀变速直线运动的合运动。
【射高】在斜抛运动中,轨迹最高点的高度叫做“射高”。它是由竖直方向的分运动决定的,求出初速度为vy的竖直上抛运动的最大高度,即可得到斜抛运动的射高。
【射程】在斜抛运动中,物体从被抛出的地点到落地点的水平距离叫做“射程”。它跟初速度v0和抛射角θ有关。利用射程的表达式,即
![]()
在抛射角θ不变的情况下,射程x与v20成正比,所以射程随初速度增大。在初速度v0不变的情况下,随抛射角θ的增大,sin2θ增大,射程也增大。当θ=45°时,sin2θ=1,射程达到最大值,以后抛射角再增大时,sin2θ减小,射程也减小。
【弹道曲线】弹头飞行时其重心所经过的路线谓之“弹道曲线”。由于重力作用和空气阻力的影响,使弹道形成不均等的弧形。升弧较长而直伸,降弧则较短而弯曲。膛外弹道学专门研究弹头在空中运动的规律,例如弹头的重心运动、稳定性等也都会影响到弹道曲线。斜抛射出的炮弹的射程和射高都没有按抛体计算得到的值那么大,当然路线也不会是理想曲线。物体在空气中运动受到的阻力,与物体运动速度的大小有密切关系:物体的速度低于200米/秒时,可认为阻力与物体速度大小的平方成正比;速度达到400~600米/秒时,空气阻力和速度大小的三次方成正比;在速度很大的情况下,阻力与速度大小的高次方成正比。总之,物体运动的速度越小,空气阻力的影响就越小,抛体的运动越接近理想情况。例如,不计空气阻力,某低速迫击炮的理想射程是360米,实际上能达到350米,空气阻力的作用处于次要地位;加农炮弹的速度很大,在不计阻力时计算的理想射程能达46公里,而实际只能达到13公里,空气的阻力是不能忽视的。
【圆周运动】质点在以原点为圆心半径为r的圆周上运动时,即其轨迹是圆周的运动叫“圆周运动”。它是一种最常见的曲线运动。例如电动机转子、车轮、皮带轮等都作圆周运动。在圆周运动中,最常见和最简单的是匀速圆周运动。
【匀速圆周运动】质点沿圆周运动,如果在相等的时间里通过的圆弧长度都相等,这种运动就叫做“匀速圆周运动”,亦称“匀速率圆周运动”。物体作圆周运动的条件:①具有初速度;②受到一个大小不变、方向与速度垂直因而是指向圆心的力(向心力)。物体作匀速圆周运动时,速度的大小虽然不变,但速度的方向时刻改变,所以匀速圆周运动是变速运动。又由于作匀速圆周运动时,它的向心加速度的大小不变,但方向时刻改变,故匀速圆周运动是变加速运动。“匀速圆周运动”一词中的“匀速”仅是速率不变的意思。
【线速度】刚体上任一点对定轴作圆周运动时的速度称为“线速度”。它的一般定义是质点(或物体上各点)作曲线运动(包括圆周运动)时所具有的即时速度。它的方向沿运动轨道的切线方向,故又称切向速度。它是描述作曲线运动的质点运动快慢和方向的物理量。物体上各点作曲线运动时所具有的即时速度,其方向沿运动轨道的切线方向。在匀速圆周运动中,线速度的大小等于运动质点通过的弧长(S)和通
![]()
线速度的大小虽不改变,但它的方向时刻在改变。它和角速度的关系是v=ωR。线速度的单位是米/秒。
【角速度】连接运动质点和圆心的半径在单位时间内转过的弧度叫做“角速度”。角速度的单位是弧度/秒,读作弧度每秒。它是描述物体转动或一质点绕另一质点转动的快慢和转动方向的物理量。物体运动角位移的时间变化率叫瞬时角速度(亦称即时角速度),单位是弧度·秒-1,方向用右手螺旋定则决定。对于匀速圆周运动,角速度ω是一个恒量,可用运动物体与圆心联线所转过的角位移Δθ和所对应的时间Δt之比表示
![]()
【向心力】物体在作圆周运动时,必然有一个方向跟速度方向垂直指向圆心的力作用于作圆周运动的物体上,这种力叫做“向心力”。此力的数值等于质点质量m和其运动速率v平方的乘积除以曲率半径r,
![]()
所受的合力;若质点沿曲线运动的速率不是常数,则质点所受合力不再指向曲率中心,向心力为质点所受合力沿曲线主法线方向的分量(另一分量沿切线方向)。当质点作圆周运动时,向心力指向圆心,曲率半径即为圆的半径。向心力不是什么“特殊的力”,更不是质点“作圆周运动时产生的力”。它是弹力、摩擦力、重力、电场力、磁场力或这些力的合力沿法线方向的力,是由于它的作用产生加速度的方向始终指向曲率中心而得名。作匀速圆周运动的物体向心力就是物体所受的合力,作非匀速圆周运动物体向心力是物体所受的合力在径向的分力。在解答有关圆周运动向心力的问题时,应注意下列几点:
1.向心力的作用只是使物体不断改变运动方向,而不改变力的大小;
2.在一般情况下,作用于作圆周运动的物体的力不止一个,当有n个力同时作用时,向心力就是n个力的合力;
3.向心力和离心力是一对作用力和反作用力,作用于两个不同的物体上,因而不能平衡;
4.在不同情况下,各种力都可以作为向心力来使物体作圆周运动,也就是说,向心力可以是重力,也可以是弹力、摩擦力、电磁力等。
![]()
当v相同时,Fn跟r成反比;Fn=mω2r说明,当ω相同时,Fn跟r成正比,这两个公式并不矛盾。
计算向心力的大小,可用上述两个公式。向心力F跟圆半径r的关系是:在线速度v一定的条件下,F与r成反比;当角速度ω一定时,F与r成正比,两者并不矛盾,不能脱离线速度或角速度来讨论向心力F跟圆半径r的关系。
【离心力】它是向心力的反作用力。向心力是外界作用于作圆周运动物体上的力,它的反作用力是作圆周运动的物体施于外部物体上的力,其方向背向圆心,所以叫“离心力”。向心力和离心力是作用力与反作用力,它们大小相等、方向相反,作用于两个不同的物体上。它和向心力同时产生、同时消失。离心力与惯性离心力有区别。(见惯性离心力)
【惯性离心力】在相对于地面作匀速转动的圆盘(非惯性系)上,用弹簧将一个质量为m的小球与圆盘的中心相连,如图1-17所示。当圆盘以角速度ω转动时,盘上的观察者将发现小球m受一个力的作用向外运动从而把弹簧拉长,即小球受到一个方向背离旋转中心的作用力,此力是小球的惯性引起的,故称“惯性离心力”。它的大小为
f惯=mω2r
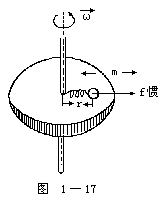
惯性离心力是转动参照系(圆盘)中的观察者,在不知道系统作圆周运动的情况下,为解释他所观察到的现象而引入的一个假想力,而不是惯性系中的观察者看到的作圆周运动的小球施于弹簧上的离心力。人们对向心力、离心力、惯性离心力很容易混淆。如图1-17所示。绳子给予小球的拉力F=mω2r,给小球提供了作匀速圆周运动所必需的向心力。根据牛顿第三定律,小球也以F'=mω2r的力拉绳子,这个力与向心力的方向相反,背离圆心,称为离心力。这个向心力和离心力是从惯性参照系来看圆周运动时所引入的两种不同概念的力。上图所示的装置,一旦绳子断掉,维持小球作圆周运动的向心力消失(离心力也同时消失),小球由于惯性,将保持原有的运动速度,沿圆周的切线方向飞去。可见,惯性离心力是从非惯性系来看力学现象而引入的一个概念,它和上述离心力的概念是完全不同的。
【圆锥摆】圆锥摆是用于研究向心力的装置。细绳长为L,在细绳的下端拴一个质量为m的小物体,手握绳子的上端,使小物体在水平面内做圆周运动,细绳沿圆锥而旋转,这就是一个圆锥摆。当物体绕圆周运动时,细绳即在沿圆锥面旋转。增大小物体绕圆心O匀速旋转的角速度为ω,可看到绳跟竖直方向的夹角θ随着增大。做匀速圆周运动的小物体m受到地球对它的重力G和绳对它的拉力T的作用,G和T的合力F就是使m产生向心加速度的向心力。圆锥摆细绳跟竖直方向的夹角θ与
![]()
![]()
【超重】当物体向上作加速度运动时,它对支持物的压力(或拉力)大于物体所受重力的现象,谓之“超重”。人造地球卫星在发射时,有一个向上的加速度,使舱内一切物体对支持物的压力增大(超过物体所受的重力),又如电梯加速上升,或减速下降都有这种现象。公式表示为T=G+ma。
【失重】当物体存在向下的加速度时,它对支持物的压力(或拉力)小于物体所受重力的现象,谓之“失重”。当人造地球卫星进入轨道后,绕地球做圆周运动,在地球引力作用下产生一个指向地球中心的向心加速度,大小等于重力加速度g,此时卫星上的一切物体对支持物的压力为零,并处于完全失重状态。应该明确,无论物体处于何种状态(超重或失重),地球对物体的重力作用始终存在,且大小亦无变化,只是物体对支持物的压力或拉力发生了变化。
【离心运动】做匀速圆周运动的物体,在合外力突然消失或者合外力不足以提供所需的向心力时,将做逐渐远离圆心的运动,此种运动叫“离心运动”。在半径不变时物体作圆周运动所需的向心力,是与角速度的平方(或线速度的平方)成正比的。若物体的角速度增加了,而向心力没有相应地增大,物体到圆心的距离就不能维持不变,而要逐渐增大使物体沿螺线远离圆心。若物体所受的向心力突然消失,即将沿着切线方向远离圆心而去。人们利用离心运动的原理制成的机械,称为离心机械。例如离心分液器、离心节速器、离心式水泵、离心球磨机等都是利用离心运动的原理。当然离心运动也是有害的,应设法防止。例如砂轮的转速若超过规定的最大转速,砂轮的各部分将因离心运动而破碎。又如火车转弯时,若速度太大会因倾斜的路面和铁轨提供给它的向心力不足以维持它作圆周运动,就会因离心运动而造成出轨事故。
【弧度】平面角单位。它是国际单位制的两种辅助单位之一,是测量角度所用的单位,是圆内两条半径间的平面角,这两条半径在圆周上截取的弧长与半径相等。符号为rad。
【开普勒三定律】
第一定律(轨道定律):所有行星都沿各自的椭圆轨道运动,太阳在该椭圆的一个焦点上。
第二定律(面积定律):太阳和运动着的行星之间的联线,在相等的时间内扫过的面积总相等。
第三定律(周期定律):各个行星绕太阳公转周期的平方和它们的椭圆轨道的半长轴的立方成正比。
开普勒总结了丹麦天文学家第谷·布拉赫对天体精确观测的记录,经过辛勤的整理和计算,归纳出行星绕太阳运行的三条基本规律。开普勒定律只涉及运动学、几何学方面的内容。开普勒定律为万有引力定律的提出奠定了基础,此三定律也是星球之间万有引力作用的必然结果。
【万有引力】自然界存在的四种基本力之一。它是物质的一种基本属性。宇宙间任何两个质点之间存在的相互吸引力,称为“万有引力”。牛顿在开普勒行星运动三定律的基础上,首先肯定了这种引力的存在,地球对地面上附近的物体有吸引力(即重力)。将地球近似地看作各层质量均匀分布的球体,则地面上物体所受地球的引力可用公式
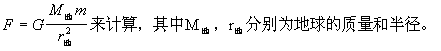
【万有引力定律】任何两物体间都存在相互作用的引力,引力的大小(F)与两物体质量m1、m2的乘积成正比,与两物体间的距离(r)的平方成反比;引力的方向是沿两个物体的联线方向。数学表达式为:
![]()
式中G是对所有质点都有相同数值的普适常数,称为万有引力常数或万有引力恒量,简称引力常数或引力恒量。在国际单位制中,G的公认值是G=6.67×10-11牛·米2/千克2。牛顿运用开普勒定律提供的实验数据,以及自已在力学L的成就,进行了长期的观察、分析、研究,于1687年正式发表了这一著名的万有引力定律。这一定律中的物体指的是质点。如物体不能被看作是质点时,可看作是质点组,构成两物体的所有质点间引力的合力,才是两物体相互吸引的力。只有在这种情况下,定律中的两物体的“连线方向”、“两者之间的距离”等才有确定的意义。如果两物体是质量均匀分布或者各层的质量是均匀分布的球体时,可将此物体的质量看成集中于球心。
20世纪以来发现在微观世界或高速运动的物体之间牛顿万有引力定律将出现微小的差异,因此,爱因斯坦提出广义相对论,对牛顿万有引力理论进行了修正。
【万有引力恒量】又叫重力恒量。用G表示这一常数。它是在牛顿发现万有引力定律一百多年以后,由英国物理学家卡文迪许于1798年用扭秤测定的万有引力常数,从而算出地球的质量和密度。卡文迪许扭秤的主要部分是一个倒挂在石英丝下端的T形架,T形架水平杆的两端各装一个质量为m的小球,T形架的竖直杆上装一块小平面镜,用它将射来的光线反射到一根刻度尺上。再将两个大球分别放在小球附近,并且跟小球的距离相等。由于小球受大球的吸引,石英丝被扭转。扭转的角度,可从小镜反射光在刻度尺上移动的距离求出,即可对两球的引力进行计算。为防止气流的影响而将扭秤置于密闭室内,用望远镜在室外进行观测。
多次实验证明牛顿的万有引力定律不但正确,而且测出了万有引力恒量是6.754×10-11牛·米2/千克2,它同现在国际上公认的G值等于6.67×10-11牛·米2/千克2很接近。这一数值等于两个质量各为1千克的物体,相距1米时的相互吸引力。
【地球上物体重力的变化】物体的重力是受地球引力的作用所致,但重力并不等于地球对物体的万有引力。其原因是因为地球在不断地自转,如以太阳作参照系来观察(太阳是惯性参照系),
![]()
地面上的一切物体随地球转动而作匀速圆周运动的角速度亦为ω。这些物体作匀速圆周运动的圆周平面垂直于地轴而和纬线相吻合。作匀速圆周运动的物体所需之向心力,是地球对物体的万有引力的一个分力,它使物体作匀速圆周运动。如图1-18所示,设物体m所在处地球的纬度为φ。F是地球对物体的万有引力,方向指向地心O,地球以角速度ω绕地轴自西向东自转。现将F分解为Fn和P两个分力。Fn的方向指向物体m作圆周运动的圆心O',它的大小等于物体m作圆周运动所需要的向心力,即Fn=mω2r=mω2Rcosφ。可见,物体所需要
![]()
量,M是地球的质量)。F的方向指向地心O。利用平行四边形法则,可求另一分力P,即使物体在自由落体运动中产生重力加速度的力,由于P的存在使物体对支持物产生压力,对悬绳产生拉力。P就是物体所受的重力,它并不指向地心,也不等于地球对物体的万有引力F。物体所受的重力随地域纬度的增大而增大。又因为地球是椭圆体,它的极半径(6357千米)比平均半径(6370千米)小,而赤道半径(6378千米)比平均半径大。根据万有引力与距离平方成反比的关系,物体在赤道处所受的万有引力F就要比两极处受到的万有引力小。上述是以太阳作参照系,立足于惯性系。若以地球作参照系,则从地球这个非惯性系的角度来考虑,一定会受到如图1-19所示的惯性离心力f。f的方向与向心加速度的方向相反,背离轴心。f的大小等于mω2r=mω2Rcosφ。此
![]()
地球对物体的万有引力F和惯性离心力f的合力P,即为物体所受的重力。两种分析方法所得物体重力是相同的。所以同一物体在赤道上的重力最小,用弹簧秤称出的重量最轻,在两极处恰恰相反。同一物体在赤道和两极重量的比较,变化并不太大,增加部分约为原重的5/1000。

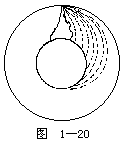
【人造地球卫星】凡火箭、太空航具,或其他人造物体经设计并置于绕地球运转之轨道上者,均称为“人造地球卫星”。人造卫星是牛顿在他《Principin》一书中所拟出来的理想实验,图1-20是从他的书上复印出来的。从一山顶射出来的子弹,当它们的初速度愈快,离山脚的距离就愈远。当速率足够高时,它将绕地球作圆周运动。
人造地球卫星绕地球运行的轨道为圆形或椭圆形两种。若使卫星沿圆形轨道运行,必须注意发射方向一定要水平,发射速度必须等于圆形轨道速度,如有稍许偏差,必不能成圆形轨道。椭圆形轨道对发射角度与速度无上述限制,但其近地点应在300千米以上,远地点应在2000千米以上。若近地点在300千米以内会受稀薄大气阻力,而使卫星失速而坠落。据测试卫星的近地点如在500千米以上,运行时间可维持在一年以上。如近地点恰在300千米的高度,则只能维持半月之久。若其近地点只达160千米,恐运行不满一周,即因大气阻力而使之坠落。据资料判定,假定近地点在500千米高度,大约可维持5~10年,这需要用事实来判断。
【宇宙速度】物体脱离地球,不同程度地进入太空所需要的最小速度称为宇宙速度。在地球表面发射人造卫星,运用牛顿运动定律和万有引力定律,设卫星质量为m,离地心高度为r,地球的质量是M。卫星的速度是v,卫星做匀速圆周运动所需的向心力是地球对它的引力,即
![]()
式中r越大,卫星离地面越高,它环绕地球运动的速度v越小。靠近地面运转的卫星,可认为r差不多等于地球的半径R地,地球对卫量的引
![]()
![]()
在地球引力作用下,在半径等于地球半径的圆形轨道上飞行的人造卫星的速度v1是
![]()
式中g是地球的重力加速度(g≈9.8米/秒2),R是地球的平均半径(R≈6400千米),则这一速度值为:v1≈7.9×103米/秒,叫做第一宇宙速度,亦称“环绕速度”。
当抛体的初速度继续增加时,它的运行轨道不再成闭合曲线,而成为抛
物线或双曲线,这时抛体将脱离地球的引力范围,成为围绕太阳运行的人造行星。若不计空气阻力,抛体脱离地球运行的最低速度,叫做第二宇宙速度,亦称“脱离速度”。第二宇宙速度
![]()
![]()
它的数值约等于11.2×103米/秒。当物体在地球表面附近以大于第一宇宙速度和小于第二宇宙速度被抛出,它将环绕地球作椭圆轨道运动。地球中心是这椭圆轨道的一个焦点,且抛射点是椭圆轨道上距离地球中心最近的一点,称为近地点。
物体能够挣脱太阳系引力的束缚,进入宇宙空间去,它所需的最小速度,叫第三宇宙速度,亦称“逃逸速度”。若不计空气阻力,则它的数值约为16.7×103米/秒。
【静止】在力学中,一个物体相对于另一个物体的相互位置不发生变化,则称这两个物体处于相对静止状态。通常所说的物体静止,是以地球为参照物,相对于地球而言的。例如,地面上的树木、房屋、停驶的汽车与地面没有发生位移的变化,均属于静止的物体。静止是物体的加速度为零,速度也等于零的运动的特殊形式。
【相对静止】没有任何方法可以证实一个物体是在绝对静止之中。绝对静止的物体是不存在的。静止只是一个物体对于它周围的另一个参照物保持位置不变,所以也只能是相对静止和相对运动。判断一个物体是在静止中还是在运动中,必须选择合适的参照物。选择的参照物不同,物体的运动状态就不同。例如,坐在火车里的人若以火车作参照物,则他看到火车上的货物对火车的位置不变,故货物对火车相对静止。若选地面上的树木或建筑物为参照物,人看到货物对建筑物的位置是不断变化的,故货物对树木做相对运动。
【相对运动】一物体相对另一物体的位置随时间而改变,则此物体对另一物体发生了运动,此物体处于相对运动的状态。如果相互之间的位置并不随时间而改变,则此物体即在相对静止状态之中。因此,静止与运动两者都是相对的概念,与物体相对于选定的参照物有关。一栋楼房或一棵树对地球来说,它们是静止的;但对太阳来说,它们却都在运动着。当一列火车经过车站时,我们就说这列火车相对车站而运动。但是对在火车上的旅客,可以认为车站是在与火车运行相反的方向相对火车而运动。所以,在描述物体是否运动时,观察者必须选择一个参照物,然后根据所选定的参照物来确定物体是否运动。
【拉力】在弹性限度以内,物体受外力的作用而产生的形变与所受的外力成正比。形变随力作用的方向不同而异,使物体延伸的力称“拉力”或“张力”。
【推力】由火箭或喷气引擎加于宇宙飞船上的反作用力,其大小决定于燃料燃烧情况以及燃气喷出之速度。在地球上发射宇宙飞船时,火箭的推力必须比飞船及火箭本身的重量大,才能使其升空,所以如果送质量较大的宇宙飞船由地球进入轨道时则需用较大推力的火箭。又如举重运动员将杠铃向上推举所用之力称为“推力”。
【阻力】妨碍物体运动的作用力,称“阻力”。在一段平直的铁路上行驶的火车,受到机车的牵引力,同时受到空气和铁轨对它的阻力。牵引力和阻力的方向相反,牵引力使火车速度增大,而阻力使火车的速度减小。如果牵引力和阻力彼此平衡,它们对火车的作用就互相抵消,火车就保持匀速直线运动。物体在液体中运动时,运动物体受到流体的作用力,使其速度减小,这种作用力亦是阻力。例如划船时船桨与水之间,水阻碍桨向后运动之力就是阻力。又如,物体在空气中运动,因与空气摩擦而受到阻力。
【压力】垂直作用在物体表面上的力叫作“压力”。力可以使物体产生形变。例如,用木棒从各个角度挤压面团,可看到,当木棒离开后,面团上留下一个个的凹坑,这种使面团发生凹陷形变的力为压力。压力是垂直作用在物体表面上,使物体表面凹陷的力。其中“作用在物体表面上”一语,意味着表面上各点都是压力的作用点,“垂直物体表面”是压力的方向,“使物体表面凹陷”是压力产生的作用效果。例如按图钉,其方向可以与墙面垂直,可与天花板垂直,也可与水平桌面垂直,无论这个面如何放置,压力的方向总是要与接触面相垂直的。这是与其他力的一个根本区别。
【压强】垂直作用于物体的单位面积上的压力。若用P表示压强,
![]()
单位为帕斯卡(1帕斯卡=1牛顿/米2)。
对于压强的定义,应当着重领会四个要点:
1.受力面积一定时,压强随着压力的增大而成正比例地增大。
2.同一压力作用在支承物的表面上,若受力面积不同,所产生的压强大小也有所不同。受力面积小时,压强大;受力面积大时,压强小。
3.压力和压强是截然不同的两个概念:压力是支承面上所受到的并垂直于支承面的作用力,跟支承面面积大小无关。
4.压力、压强的单位是有区别的。压力的单位是牛顿,踉一般力的单位是相同的。压强的单位是一个复合单位,它是由力的单位和面积的单位组成的。在国际单位制中是牛顿/米2,称“帕斯卡”,简称“帕”。
【压力和重力】压力和重力是两个不同的概念。它们的施力物体,以及力的大小、方向、作用点都有区别。重力的施力者是地球,方向(永远)竖直向下,作用点在物体的重心上。压力的施力者是与受力物体接触的其他物体,本质是弹力,方向(永远)垂直于受力物体表面,作用点在受力物体的表面上。可见,压力和重力是两种完全不同的力。只有在某些情况下,压力和重力在数值上是相等的。如物体压在水平地面上时,其重力与压力相等。
【帕斯卡】简称“帕”代号Pa。为纪念帕斯卡而作为单位名称,他发现大气压强随高度而变化。帕斯卡是国际单位制中压强P的单位。1帕斯卡的压强等于1米2的面积上均匀作用1牛顿的力所产生的压强,即1帕=1牛顿/米2。它跟气体压强中其他单位的关系为:1标准大气压=76厘米汞柱高=1.013×105帕斯卡。
【帕斯卡定律】由于液体的流动性,加在密闭液体上的压强,能够按照原来的大小由液体向各个方向传递。这个定律在生产技术中有很重要的应用,例如液压机,液压传递都是根据这一定律制成和工作的。这一定律是法国物理学家帕斯卡首先提出的。
【液体内部压强】液体内部压强的特点是:液体具有重量;液体具有流动性。由于液体有重量,因此在液体的内部就存在由液体本身的重量而引起的压强,从实验结果及理论推证都表明,这个压强等于液体单位体积的质量和液体所在处的深度的乘积,即P=ρgh(式中g=9.8牛顿/千克)。由公式知,液体内部的压强与深度有关,深度增加,压强亦随着增加。
因为液体具有流动性,所以液体内部的压强又表现出另外一些特点:液体对容器的底部和侧壁都有压强的作用,而且压强一定与底面或侧壁垂直;液体内部的压强是向各个方向的,而且在同一深度的地方向各个方向的压强都相等。在解题时应注意下列几点:
1.液体内部某处的深度h,应当取该处至液面的垂直距离,它与容器的形状无关。
2.深度与高度是有区别的,深度是从液面向下至某一点的垂直距离,而高度是从容器或液体的底部起向上数到液面的竖直高度。
3.液体内部某处至液面之间有几层密度不同的液体,则该处的压强等于几层液体各自产生的压强之和。在考虑大气压的情况下,还应当加上液面上受到的大气压。
4.连通器中的液体在平衡时左管中液体的压强一定与右管中液体的压强相等。
【液体对容器的压强】液体内部存在压强,压强的大小与液体的深度和液体的密度有关,即P=ρgh。由于液体具有流动性,当液体装入容器中时,容器的底和壁就要受到液体的压强。
1.液体对容器底部的压强:在各种不同形状的容器中,如只装同种液体,只要液柱的竖直高度相等,液体对容器底部的压强就相等。它与容器的形状、容积以及底面积的大小无关,更不管所盛液体重量的大小。
液体对容器底部的压强与容器底对支承面的压强不同。例如,三个质量相同。底面积相同的不同容积的容器,装入同种而且高度亦相同的液体,静止放在水平的桌面上,根据公式ρgh,三个容器底部所受的液体压强是相等的。桌面受到的压强,是盛着液体的容器压在桌面上而产
![]()
所盛液体重量不等,桌面上所受的压力就不相等。尽管桌面的受力面积相同,桌面所受的压强是不会相等的。
如果一个容器中装有几种不相溶混的液体,该容器底部所承受的压强,应是几种液体压强相加。因为下面的液体被上面的液体所封闭,根据帕斯卡定律,密闭的液体会将上面液体的压强传至容器的底面,因此容器底所受之压强是P1+P2+…=P总。
2.液体对容器侧壁的压强:容器侧壁处于不同的深度,各点所受之
![]()
![]()
【流体】是液体和气体的总称。流体是由大量的、不断地作热运动而且无固定平衡位置的分子构成的,它的基本特征是没有一定的形状和具有流动性。流体都有一定的可压缩性,液体可压缩性很小,而气体的可压缩性较大,在流体的形状改变时,流体各层之间也存在一定的运动阻力(即粘滞性)。当流体的粘滞性和可压缩性很小时,可近似看作是理想流体,它是人们为研究流体的运动和状态而引入的一个理想模型。
【流体力学】研究流体的运动规律以及流体与流体中物体之间的相互作用。在流体力学中一般不考虑流体的分子、原子结构而把它看作连续介质。它处理流体的压强、速度及加速度等问题,包括流体的形变、压缩及膨胀。因此流体力学也是以牛顿运动三定律为基础的,并遵循质量守恒,能量守恒和功能原理等力学规律。流体力学又分为流体静力学和流体动力学,在中学教材中,只涉及到流体静力学的内容。
【流体静力学】流体处于不流动的静止状态,称为流体处于平衡状态。研究流体静止条件及关于物体在流动中受力情况的力学称为“流体静力学”。其研究的主要内容有:密度、压强、液体内部压强、大气压强、帕斯卡定律、浮力及阿基米德定律等。
【流体动力学】研究运动流体的宏观状态和规律的学科。主要研究对象包括流体的速度、压强、密度等的变化规律,粘滞流体的运动规律及粘滞流体中运动物体所受的阻力,以及其他热力学性质。
【液体之表面】静止的液体,其表面永远趋于水平状态,否则其表面必将高低不平。设某一大容器内B处液面比A处液面高h米,而液体之密度为ρ,则在与A处于同一水平面上而又在B下之C点,所受之压强较A处之压强大ρgh,于是C点之液体必向A处流动。此时的液体不是静止而是处于流动状态,直至液面处于水平状态。这就是静止的液体表面永远趋于水平的道理。
【水压】指水的压力。用容器盛水时,由于水有重量,就有相当于那么多重量的压力,向容器的壁及底面作用。盛在容器中的水,对侧面及底面都有压力作用,对任何方向的面,压力总是垂直于接触面的。而且深度相同时,压强也相同;液体越深,则压强也越大。例如,在一个两端开口的玻璃管的一端加一薄塑料片,开口一端向上,直放入水中时,薄片不会下落。这是因为有水向上托之力(即向上的压力)。然后将水慢慢地一点点灌入玻璃管中,管内的水面未接近管外的水面时,塑料薄片不会掉下。这证明水有向上的压力,给薄片一个支持的力。继续加水至管内外水面相平时,管内水柱向下的压力与管外薄片受到的向上压力相等,由于塑料薄片本身的重量而落下。此时,筒底薄片所受之向下的压力是筒中水柱的重量,所受之向上的压力,为筒所排除水的重量,二者相等而方向相反,遂相消而等于零,薄片是受重力作用而落下。如将玻璃管倾斜放置,其结果也是一样。即水的压力向上,各侧面都有压力作用。
【液体的压力】液体受到重力作用,而向下流动,因受容器壁及底的阻止,故器壁及底受到液体压力的作用。如图1-21所示,为一竖直之容器,器底阻止液体向下流动,故等于液体重量的力向下压器底,器底面cd部分所受的压力等于abcd液柱之重。
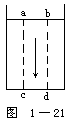
液体因为重力的作用和它的流动特性,当液体静止时液体内以及接触面上各点所受的压力,都遵守下列各条规律:
1.静止液体的压力必定与接触面垂直。
2.静止液体内同一水平面上各点,所受压强完全相等。
3.静止液体内某一点的压强,对任何方向都相等。
4.静止液体内上下两点的压强差,等于以两点间的垂直距离为高度,单位面积为底的液柱重量。
前面曾提到静止液体的压力与液体重量的关系。但那是有条件的,因为容器筒壁是竖直的。如果有三个形状不同的容器A、B、C,底面积相同都为S,而且装有相同高度h的同种液体。在这种条件下静止液体的压力,是否一定等于液体的重量?对图1-22所示情况进行分析,根据上述条件,则:
PA=PB=PC=ρgh
FA=FB=FC=ρghS

但是三个容积大小不等,B的容积大于A,C的容积小于A。由于三个容积大小不同,尽管高度相同,但所盛液体的重量并不相等,所以有GB>GA>GC。尽管液重不同,但它们底部所受的压力却相等。因液体是流体,会流动,对容器的四壁都要产生压强。A容器的液体重量竖直方向落在SA上,只有容器A静止液体的压力与液体重量相等。其他两容器则不然,B容器里液体的重量虽然很大,但真正作用在容器底面上的压力,只有图中虚线部分所包围的液柱的重量,和容器A底面上所受的压力一样,FB=FA,虚线外的那部分液体的重量,作用在斜壁上面。容器C由于h'液柱压强的作用,而使容器“肩部”的内壁对液体产生压力F'。如果用S'表示一个“肩部”的横截面积,那么F'=ρgh'S'。这个压力F',正好就是“肩部”和容器A相比所缺少的那部分(图中虚线部分)液体的重量。“肩部”的压力F',都要被液体传递到容器的底部。所以,容器C的底部所受到的压力要比容器里的液体重量大,它等于以容器底为底的液柱的重量,即FC=FA。
从以上情况可见,不管容器的形状是怎样的,只要容器中装的是同一种液体,深度相同,而且底面积也相同,即使它们的重量不等,但是容器底部所受到的压力必定相等。所以,静止液体的压力,并不一定就等于液体的重量。在求静止液体产生的压力时,就应该用压强乘受力面积,即F=ρghS。
【液压机】利用帕斯卡定律制成的利用液体压强传动的机械,种类很多。当然,用途也根据需要是多种多样的。如按传递压强的液体种类来分,有油压机和水压机两大类。水压机产生的总压力较大,常用于锻造和冲压。锻造水压机又分为模锻水压机和自由锻水压机两种。模锻水压机要用模具,而自由锻水压机不用模具。我国制造的第一台万吨水压机就是自由锻造水压机。
【液压机原理】它是由两个大小不同的液缸组成的,在液缸里充满水或油。充水的叫“水压机”;充油的称“油压机”。两个液缸里各有一个可以滑动的活塞,如果在小活塞上加一定值的压力,根据帕斯卡定律,小活塞将这一压力通过液体的压强传递给大活塞,将大活塞顶上去。设小活塞的横截面积是S1,加在小活塞上的向下的压力是F1。于是,
![]()
体上的压强,能够大小不变地被液体向各个方向传递”。大活塞所受到的压强必然也等于P。若大活塞的横截面积是S2,压强P在大活塞上所
![]()
![]()
![]()
在小活塞上加一较小的力,则在大活塞上会得到很大的力,为此用液压机来压制胶合板、榨油、提取重物、锻压钢材等。
【万吨水压机】它是我国自己设计制造的第一台大型自由锻造水压机,于1961年由上海江南造船厂制成投入生产。这在当时的生产条件,以及生产设备来看,确是惊人的创举。这种大型水压机可以产生上亿牛顿的压力,它能把九百吨,以至上千吨加热后的钢材像揉面似的压制成各种不同形状的钢件。这种经过锻压过的铁块,其内部变得密实、均匀,而且有韧性,制成车轴、车轮等不易断裂。是造船厂以及重型机械制造厂在生产上不可缺少的设备。这台水压机有两个特点:其一是既重又大,它的主机重2200多吨,高23.6米,基础深入地下40米,共有4万多个零件,其中有13个大件,6个主缸,4根大立柱,3个大横梁。水压机的4根大立柱每根大约有18米高,1米粗,80吨重。每根立柱都有几个大螺帽,一个大螺帽就有5~6吨重。三个大横梁(上横梁,下横梁,动横梁)每个都有几百吨重。其二是精密,3500牛顿/厘米2的高压水要用12台高压水泵,16个高压容器和100多个高低压阀门进行联动控制,有关机件都必须有高度的精密性、密封性、准确性和灵活性。万吨水压机一般用于锻造、冲压、挤压、拉伸、起重、打包等需要较大压力的工作。如,锻造大型发电机转子轴、大型轧钢机机架、万吨轮发动机主轴、炮管、导弹外壳等特大型的机件。
【油压千斤顶】它是生产中常用的一种起重工具。它的构造简单、操作方便,修理汽车、拖拉机等常用它将车身顶起,便于修理。油压千斤顶是根据帕斯卡定律的原理工作的。它由油箱,大小不同的两个压力油缸、摇杆和关闭针阀等几个部分组成。工作时,提起小活塞将油吸入小压力油缸,当压下小活塞时将油压进大压力油缸。通过两个阀门的控制,小活塞对油的压强传递给大活塞,将重物顶起来。小活塞不断地往复动作,就可以把重物顶到一定的高度。工作完毕,打开关闭针阀,使大压力油缸和油箱连通。这时,只要在大活塞上稍加压力,大活塞即可下落,油回到油箱中去。
【连通器】几个底部互相连通的容器,注入同一种液体,在液体不流动时连通器内各容器的液面总是保持在同一水平面上。连通器的原理可用液体压强来解释。若在U形玻璃管中装有同一种液体,在连通器的底部正中设想有一个小液片AB。假如液体是静止不流动的。左管中之液体对液片AB向右侧的压强,一定等于右管中之液体对液片AB向左侧的压强。因为连通器内装的是同一种液体,左右两个液柱的密度相同,根据液体压强的公式P=ρgh可知,只有当两边液柱的高度相等时,两边液柱对液片AB的压强才能相等。所以,在液体不流动的情况下,连通器各容器中的液面应保持相平。
连通器的特点是只有容器内装有同一种液体时各个容器中的液面才是相平的。如果容器倾斜,则各容器中的液体即将开始流动,由液柱高的一端向液柱低的一端流动,直到各容器中的液面相平时,即停止流动而静止。如用橡皮管将两根玻璃管连通起来,容器内装同一种液体,将其中一根管固定,使另一根管升高、降低或倾斜,可看到两根管里的液面在静止时总保持相平。其原理在生产实践中有着广泛的应用,例如,水渠的过路涵洞、牲畜的自动饮水器、水位计,以及日常生活中所用的茶壶、洒水壶等都是连通器。
【水位计】水位计也叫“液位计”或“液面计”。因锅炉里的水在高温时汽化供暖,水和汽的损耗较大,要不断地补充水,使锅炉里的水位保持一定的高度,水位过低,锅炉就有爆炸的危险。为了随时了解锅炉内的水位,在锅炉上都装有水位计,水位计和锅炉构成一个连通器。常用的有玻璃液位计、压强液位计、浮标液位计、电容液位计及电阻液位计等。在高温和高压下,也可采用同位素液位计。
【水渠】农田灌溉常利用江河之水,通过地面上所开之“沟”,引入农田。水渠是人工开凿的水道,有干渠、支渠之分。干渠与支渠一般用石砌或水泥筑成。
【涵洞】在水渠通过公路的地方,为了不妨碍交通,修筑于路面下的过路涵洞,让水从公路的下面流过再翻到地面上来,形状有管形、箱形及拱形等。它是根据连通器的原理,常用砖、石、混凝土和钢筋混凝土等材料筑成。
【船闸】在水位集中跌落的情况下(例如,建造闸、坝处),用以保证通航的水利工程建筑物。利用河水灌溉农田,或者利用水力推动水力发电机进行工作时需要在河流上修建拦河坝,用以提高水位。这样,河水被大坝隔断,上下游的水位差较大,航船无法通过。于是人们就利用连通器的原理,在运输频繁的江河上,在大坝的旁边修建了船闸。主要由闸室及上下游闸首所组成,闸室的两端设置闸门,用以与上下游隔开。当船下行时,先将闸室充水,待室内水位与上游相平时,将上游闸门开启,让船只进入闸室。随即关闭上游的闸门,闸室放水,待其降至与下游水位相平时,将下游闸门开启,船只即可出闸。上行时与上述过程相反。船闸须设有专门充水、放水系统及操纵闸门的设备。根据地形以及水位差的大小,船闸可做成单级或多级的。
【大气】围绕任何行星或其他天体的气体,包括围绕地球的空气。地球的大气由地面向上扩展至高空。大气垂直方向,有各种分层方法,通常根据大气中温度随高度垂直分布的特征划分为对流层、平流层、中间层、热成层和外大气层等,主要天气现象多发生在对流层内。
大气的组成,在120千米以下的高空中,大气的主要组成为:氮分子(N2)占78.00%和氧分子(O2)占20.25%的均匀混合体,其次为0.93%的氩(Ar)与0.03%的二氧化碳(C02)。再其次的组成元素(按含量的递减而排列)为氖、氦、氪、氙、氢、氯、氧化亚氮、臭氧、二氧化硫、二氧化氮、氨、一氧化氮及碘。二氧化碳及臭氧在大气中的含量虽然很少,但它们确是大气中之重要成分,因为二氧化碳可保持环境温度,臭氧则可防止太阳的某种有害人类之短波辐射至地面。大气中的水蒸气及微尘之含量,则是随高度之增加而降低,它们对于大气之变化,都有重要的作用。它们可使天气有雨、云、雾等的变化。大气组成元素的分布,在120千米以上的高空,随原子量的不同而异。在120千米以下的高空,大气组成为氮分子及氧分子的混合气体;由120千米至1000千米,氧原子占主要位置;1000至2500千米为氮层,2500千米以上的太空中为氢气,而且氢气由此一直延伸至星际太空中。
在高度距地面约120千米以下的高空中,大气是一个均匀且稳定的混合气体层,其中氮分子与氧分子为4∶1。在120千米以上,扩散作用的因素胜过混合作用,所以大气组成中的不同元素,则以原子形式分别集中在不同的高度层上。原子量最重的氧位于较低的高度,原子量较氧稍轻的原子,位于氧之上,如此类推,最轻的氢气位于最上层。在120千米以上的大气,由于太阳的辐射而引起的分解和电离作用,更增加了复杂性。大气的密度,按照其发光强度,电离层之反射能力,以及作用于人造卫星上的大气阻力等各项来看,自100千米以上密度的降低速度,远较100千米以下缓慢。大气密度在较高空所以缓慢下降的理由,可分两点:其一是由于大气温度随大气层厚度的增加而增加,即包围地球之大气层的温度愈高,则该大气层愈膨胀,其压力随厚度之降低亦愈加缓慢;其二是当高度至100千米以上时,大气的组成改变,愈向高空,其组成元素之重量愈轻,则大气的密度平均值亦因之降低。气体密度愈小,则其密度与压力依高度之下降亦愈加缓慢。在200千米以下的高空,对于密度的测量,可用火箭升高直接测量。但超过此高度后,直接测量就很困难。可通过作用在人造卫星上的大气阻力来分析,间接推算出密度。
【大气压】见“大气压强”。
【标准大气压】在纬度是45°的海平面上,温度是0℃时,相当于76厘米汞柱高的大气压,称为标准大气压。因为托里拆利实验中水银柱产生的压强可用p=ρgh来计算。式中h表示水银柱的高度,ρ表示水银的密度,g表示重力加速度。水银的密度跟温度有关,重力加速度与测量地点的高度和纬度有关,所以只给出水银柱的高度76厘米并不能确切地规定标准大气压的数值,还必须给出测量地点的高度、温度和纬度。
【大气压强】地面上空气的范围极广,常称“大气”。离地面200公里以上,仍有空气存在。虽其密度很小,但如此高的大气柱作用于地面上的压强仍然极大。人体在大气内毫不感觉受到气压的压迫,这是因为人体的内外部同时受到气压的作用且恰好都相等的缘故。
从地球表面延伸至高空的空气重量,使地球表面附近的物体单位面积上所受的力称为“大气压强”。大气压强的测量通常以水银气压计的水银柱的高来表示。地面上标准大气压约等于76厘米高水银柱产生的压强。由于测量地区等条件的影响,所测数值不同。根据液体压强的公式P=ρgh,水银的密度是13.6×103千克/米3,因此76厘米高水银柱产生的压强是P=13.6×103千克/米3×9.8牛顿/千克×0.76米=1.013×105牛顿/米2=1.013×105帕斯卡。
【托里拆利实验】是在17世纪,意大利数学家及物理学家托里拆利所做的一个著名实验。1643年发明了水银气压计原理,首次造成真空状态,轰动了当时。托里拆利通过实验首先测出大气压的值。在一根长约1米一端封闭的玻璃管(称“托里拆利管”)内,灌满水银,用食指堵住开口的一端,把管子倒立在水银槽里。然后放开手指,管内的水银面下降到比水银槽中水银面大约高于760毫米处就不再下降了,与当时当地的大气压强的作用平衡。若将玻璃管倾斜,进到管里的水银就多些,尽管此时水银柱的长度增加了,但是管内外水银面的高度差仍保持原来的数值不变。如将管从水银槽里提起20毫米或将管向槽里按入20毫米,管内水银柱的高度,仍保持原来数值不变。在实验时可换用管径不同的玻璃管,其结果仍然不变。
【托里拆利真空】托里拆利实验中充满水银的玻璃管,倒置于水银槽中,水银下降至一定高度即停止降落,这是因为管内的水银重量被作用于水银槽而上的大气压所支持。此时,在管内水银上面除了水银蒸气外,并无任何物质,因为水银蒸气的气压极低(在20℃时只有0.0012毫米水银柱),所以几乎可看作是真空,这就叫作“托里拆利真空”。现在管里水银面的上方没有空气,因此也就没有空气压强对管内液面的作用,管外水银面上所受到的大气压与管内水银柱对底面的液体压强是等值的。若玻璃管的顶端,突然破裂一个小洞,管里水银面上就受到跟管外水银面上相同的大气压,根据连通器的原理,管内外的水银面就会趋于水平状态。
【马德堡半球】亦称“马德堡圆盘”,是用来演示大气压强的仪器。1654年德国马德堡市的市长、学者奥托·格里克表演了一个最惊人的试验。他把两个铜质直径三十多厘米的空心半球紧贴在一起,两半球的对口处经过研磨。在贴在一起之前,应用抹布将对口处擦净,并涂上凡士林,两半球接触后,要用力压一下并稍稍左右转动一下。然后打开阀门,并用胶皮管把气嘴跟抽气机相连接,将球内气体抽出后,球外的大气压使两半球合在一起。在半球的两侧各装有一个巨铜环,环上各用八匹马向两侧拉动,结果用了相当大的力却未拉开。球内的空气被抽出,没有空气压强,而外面的大气压就将两个半球紧紧地压在一起。通过上述实验不仅证明大气压的存在而且证明大气压是很大的。这个实验是在马德堡市进行的,因此将这两个半球叫“马德堡半球”,而将这个试验叫“马德堡半球实验”。后来各学校物理实验室所用的是铸铁制成直径10厘米左右的两半球体,目前教学仪器改进而用硬橡胶制成扁圆形的半球体,省去了用抽气机抽气的装置。实验时只要将两半球紧压,将球体内空气挤出即可,也能说明球内外具有压强差。市场商店出售的塑胶制品的挂衣钩,也是根据上述实验及其原理而制成的。
在解释实验原理时应注意:拉开马德堡半球的力并不是大气压乘以球的“表面积”。作用在马德堡半球的表面上的大气压,其中有一部分作用是互相抵消的,所产生的压紧半球的力,不等于大气压强乘球的表面积,而是等于大气压强乘球的横截面积。
【气压计】根据托里拆利的实验原理而制成,用以测量大气压强的仪器。气压计的种类有水银气压计及无液气压计。其用途是:可预测天气的变化,气压高时天气晴朗;气压降低时,将有风雨天气出现。可测高度。每升高12米,水银柱即降低大约1毫米,因此可测山的高度及飞机在空中飞行时的高度。
【水银气压计】利用托里拆利管来测定大气压的一种装置。玻璃管底部的水银槽是用一个皮囊所代替,并附有可以调准的象牙针使其指示水银面,叫做“福廷式水银气压计”,在玻璃管外面加上一个金属护套,套管上刻有量度水银柱高度的刻度尺。在水银槽顶上另装一只象牙针,针尖正好位于管外刻度尺的零点,另用皮袋作为水银槽底。使用时,轻转皮袋下的螺旋,使槽内水银面恰好跟象牙针尖接触(即与刻度尺的零点在一水平线上),然后由管上刻度尺读出水银柱的高度。此高度示数即为当时当地大气压的大小。另外还有不需调准象牙针的观测站用气压计,可测低气压山岳用的气压计,以及对船的摇动不敏感的航海用气压计。
【无液气压计】是气压计的一种。它的主要部分是一种波纹状表面的真空金属盒。为了不使金属盒被大气压所压扁,用弹性钢片向外拉着它。大气压增加,盒盖凹进去一些;大气压减小,弹性钢片就把盒盖拉起来一些。盒盖的变化通过传动机构传给指针,使指针偏转。从指针下面刻度盘上的读数,可知道当时大气压的值。它使用方便,便于携带,但测量结果不够准确。如果在无液气压计的刻度盘上标的不是大气压的值,而是高度,于是就成了航空及登山用的高度计。
【真空】是指没有任何实物粒子存在的空间,地球以及星球中间的广大太空就是真空。物理学上的真空,是指稀薄的气体状态,又可分为高真空、中真空和低真空。一般是用特制的抽气机得到真空的。它的气体稀薄程度用真空计测定,现在已能用分子抽气机和扩散抽气机得到1/1011大气压的高真空。真空在科学技术,电真空仪器,电子管和其他电子仪器方面,都有很大用途。
【低气压】我们研究气压高低问题是相对而言的,某地区气压的高低是与周围比较而说的,其中气压最低的地方,叫作“低气压中心”。四周压力较高地方的空气都会流到中心来,这正好像四周高山上的水都汇集到盆地中心去一样。北半球的低气压中心附近,风是向中心吹进,为左旋的旋涡,且吹进来的空气即向上升,而形成上升的气流,通常是天气不好。
【高气压】指比周围的气压高的地点而言,其中气压最高的地点,叫作“高气压中心”。北半球的高气压中心附近,风是以右旋的涡旋而向外吹去,所以该部分的空气较为稀薄。为补充它,空气自上空降落,形成下降气流,所以通常都是好天气。
【抽水机】抽水机又名“水泵”。离心式水泵是利用大气压的作用,将水从低处提升至高处的水力机械。它由水泵、动力机械与传动装置组成。它广泛应用于农田灌溉、排水以及工矿企业与城镇的给水、排水。为适应不同需要,而有多种类型。
【活塞式抽水机】又叫“吸取式抽水机”。机体下部的进水管插入水中,抽水机是一个圆筒,筒内装一个可以上下滑动而且跟筒壁紧密配合的活塞,筒底和活塞上各有一个只能向上开的活门v1和v2。使用时,若活塞向上移动,活门v2受到大气压的作用而关闭,因此活塞下面空气稀薄,气压小于外界的大气压。于是,低处的水受到大气压的作用推开活门v1进入筒内。当压下活塞时,筒底活门v1被水的压迫而关闭,水被阻不能向下流动,于是冲开活门v2向上,水进入筒的上部。再提起活塞时,活塞上面的水将活门v2关闭,水即从侧管流出,与此同时,井里的水又在大气压的作用下推开活门v1而进入圆管中。这样,活塞不停地上下移动,水就从管口连续不断的流出。这种抽水机的结构简单,操作方便,但出水量小,提水的高度只能达到八米左右,效率也较低。
【离心式水泵】简称“离心泵”。它是一种利用水的离心运动的抽水机械。由泵壳、叶轮、泵轴、泵架等组成。起动前应先往泵里灌满水,起动后旋转的叶轮带动泵里的水高速旋转,水作离心运动,向外甩出并被压入出水管。水被甩出后,叶轮附近的压强减小,在转轴附近就形成一个低压区。这里的压强比大气压低得多,外面的水就在大气压的作用下,冲开底阀从进水管进入泵内。冲进来的水在随叶轮高速旋转中又被甩出,并压入出水管。叶轮在动力机带动下不断高速旋转,水就源源不断地从低处被抽到高处。
【压水机】压水机采用杠杆来推动。活塞本身并没有活门,但在吸管的顶部,却有一个向上开的活门v2,第二个活门v1则装在压力管接连唧筒的开口处。提高活塞时,唧筒内便形成空气稀薄的空间,大气压将水从低处压入这个空间。在这个过程中,活门v1关闭,v2打开。当活塞向下压时,v2关闭,唧筒里面的水经由打开的活门v1,被压入压力管中,并从这个管中强烈地喷射出去。它与抽水机一样,水被正常气压压入吸水管时,最多只能抽到10.33米的高度。但是压水管做成任何长度都可以,因为压力管里的水并非是由于外界气压的作用,而是经由加在活塞上的压力所压出的。因此,压水机常被用在需要把水压高到超过10米的各种场合。此外,水在继续运动时,如需克服巨大的压力,例如供应锅炉之给水,也非应用压水机不可,所以压水机必须造得更加坚固。
【抽气机】为空气抽气机之一种,是用来抽出密闭容器内气体的机器。一般有手摇和电动两种,主要构造与吸取式抽水机相似。其动作原理与抽水机相似,只不过被抽出的物质为空气。
【压缩气体】凡需要大量气体的场所,处处都会用到压缩气体,因为在压缩情况下,就不需占用宠大的空间。例如,气体焊接金属,是用高热的火焰将两块金属板熔接起来。这种火焰乃由氢气在氧气里或是乙炔气在氧气里燃烧而得来的。灭火器中应用的是压缩碳酸气。在灭火的一瞬间,经过化学作用而产生碳酸气,以使窒息火焰的灭火液及碳酸气在强大的压力下喷射出来。利用压缩空气来推动机器的其他例子甚多,例如,混凝土击碎器以及隧道之钻机,只要能向工作地点继续送进新鲜空气的地方都可以利用。此外,压缩空气的推动力,还可用于气枪和鱼雷的发射器,若干大城市的电信局用来传送邮件(即:管邮)等方面。
【虹吸现象】由于大气压的作用,液体从液面较高的容器通过曲管越过高处而流入液面较低容器的现象。它发生的条件是曲管(虹吸管)里先要灌满液体,同时高于较高液面的液柱的压强不超过大气压。例如,汽车司机常用虹吸管从油桶中吸出汽油或柴油;河南、山东一带应用虹吸管把黄河里的水引到堤内灌溉农田;在日常生活中,如给鱼缸换水等都是。
【浮力】漂浮于流体表面或浸没于流体之中的物体,受到各方向流体静压力的向上合力。其大小等于被物体排开流体的重力。例如石块的重力大于其同体积水的重量,则下沉到水底。木料或船体的重力等于其浸入水中部分所排开的水重,所以浮于水面。气球的重量比它同体积空气的重力小,即浮力大于重力,所以会上升。这种浸在水中或空气中,受到水或空气将物体向上托的力叫“浮力”。例如,从井里提一桶水,在未离开水面之前比离开水面之后要轻些,这是因为桶受到水的浮力。不仅是水,例如酒精、煤油或水银等所有的液体,对浸在它里面的物体都有浮力。
产生浮力的原因,可用浸没在液体内的正立方体的物体来分析。该物体系全浸之物体,受到四面八方液体的压力,而且是随深度的增加而增大的。所以这个正立方体的前后、左右、上下六个面都受到液体的压力。因为作用在左右两个侧面上的力由于两侧面相对应,而且面积大小相等,又处于液体中相同的深度,所以两侧面上受到的压力大小相等,方向相反,两力彼此平衡。同理,作用在前后两个侧面上的压力也彼此平衡。但是上下两个面因为在液体中的深度不相同,所以受到的压强也不相等。上面的压强小,下面受到的压强大,下面受到向上的压力大于上面受到的向下的压力。液体对物体这个压力差,就是液体对物体的浮力。这个力等于被物体所排开的液体的重量。当一个浮体的顶部界面接触不到液体时,则只有作用在底部界面向上的压力才会产生浮力。至于一个位于容器底面上的物体,并和容器底面密切接触,那它就只能受到向下作用于物体表面的液体压力下,所以这个物体不受浮力作用,这种现象并不多,因为只要其间有一层很薄的液膜,就能传递压强,底面就有向上的压力,物体上下表面有了压力差,物体就会受到浮力。
【阿基米德定律】浸在液体(或气体)里的物体受到向上的浮力,浮力的大小等于物体排开的液体(或气体)的重力。这就是著名的“阿基米德定律”。该定律是公元前200年以前阿基米德所发现的,又称阿基米德原理。浮力的大小可用下式计算:F浮=ρ液(气)gV排。
【物体浮沉条件】物体上浮或下沉时都显示出浮力的存在。关于物体浮沉的问题,不仅是浮力问题,实际上是个运动和力关系的问题。因为浸在液体或在气体中的物体要受到两个力的作用:一个是重力;另一个是浮力。重力的方向总是竖直向下的,而浮力的方向总是竖直向上的,物体的浮沉就决定于这两个力的大小。掌握物体浮沉条件的关键就在于正确地分析浸在液体(或气体)里的物体共受到几个力的作用,而且还要明确这些力大小关系和方向关系。
1.当浮力F浮大于重力G时,物体就上浮,直到F浮=G时为止;
2.当浮力F浮小于重力G时,物体就下沉,一直沉到容器底为止;
3.当浮力F浮等于重力G时,物体处于平衡状态,静止不动。如果此时物体已全部浸没在液体里(或气体)物体就可以停留在液体(或气体)内任何深度的地方。
物体的浮沉还可以从物体和液体(或气体)的密度方面来分析:
1.当ρ物<ρ液(气)时,物体就上浮;
2.当ρ物>ρ液(气)时,物体就下沉;
3.当ρ物=ρ液(气)时,物体可以在液体(或气体)内任何位置悬浮。
因此,在分析浸在液体(或气体)中的物体上浮还是下沉时,不要只看物体本身的质量或密度如何,而要根据物体的浮沉条件来具体分析才能确定。
【漂浮】是指物体有一部分体积在液体里,另一部分体积露出液面。例如,一般树木、冰块等都属于漂浮的物体,这种物体也叫作“浮体”。浮体可以静止在液面上,也可以在液面上水平运动,例如轮船,船从河里驶入大海,船是沉下些还是浮上些?有人认为海水的密度比河水的密度大,所以船在海水中受到的浮力将比河水中受到的浮力大。此种观点是错误的。根据阿基米德定律,浮力的大小,不仅决定于液体的密度,而且还决定于物体所排开的液体的体积。因此,只有在排开相同体积的液体时,液体的密度越大,对物体产生的浮力才越大。船所排开的液体的体积是变化的,所以液体的密度大,对物体所产生的浮力不一定大。船无论是在河里,还是在海里,都是浮在液面上。根据浮体的平衡条件,河水或海水对船的浮力都应等于船的重力,又因船的重力不变,所以,河水对船的浮力等于海水对船的浮力,即:ρ河gV排河=ρ海gV排海。因为g是一个常量,而ρ海>ρ河,所以V排海<V排河,船排开海水的体积变小,船应浮起一些。可见,同一浮体不论放在什么液体中,其所受浮力都等于它自身重力,即F浮=G物。
根据F浮=ρ液gV排和G物=ρ物gV物,结果漂浮条件F浮=G物,可推出V排/V物=ρ物/ρ液。此式表明,只有ρ物<ρ液时,V排才小于V物,物体才能漂浮在液面上。由F浮=ρ液gV排及漂浮条件F浮=G物,可以得到V排=G物/ρ液g。此式表明,浮体没入液体里的体积与浮体重力成正比,与液体密度成反比。故同一物体(G物不变)在密度不同的液体里漂浮,排开液体的体积不同,没入深度也不同。这就是比重计的原理,也是轮船在淡水里和海水里航行时吃水深度(没入的深度)不同的原因。
【悬浮】悬浮是指物体在液体中既不沉底,又不露出液面,即悬浮物体的体积全部在液体里。悬浮或静止的漂浮是一种平衡状态。悬浮条件与漂浮条件,形式上虽然相同,即F浮=G物,但内容含意不同。悬浮的物体完全没入液体里,这时物体所受的浮力是最大的浮力。漂浮情况,由于V排<V物,物体所受浮力,肯定不是最大的浮力。
悬浮的物体,可在液体中的任何位置停留,例如鱼及潜水艇就可悬浮于水中。又如,浮沉子的重力等于浮力时,即可悬浮于水中。悬浮在液体中的物体或漂浮在液面上的物体,它们受到的浮力一定等于物体的重力。这就是它们的平衡条件,即F浮=G物或ρ液gV排液=ρ物gV物。
【排开】指阿基米德定律“浸在液体里的物体受到向上的浮力,浮力的大小等于物体排开的液体的重力”这段话中的“排开”。从实验知道弹簧秤下端所挂之重物,放入一个已经将水装到溢水管口的水槽中,水立即被排挤出来,流出来水的体积与物体的体积相等。即水的位置被物体所取代,而将水排挤出去。这里所提到的排开,就是被物体所取代的部分水,所以V排液=V物。如果是部分浸入,则V排液等于浸在液体中那部分物体的体积。
【上浮】指的是一种竖直向上的运动,如物体在液体里向上浮起来。上浮的物体是因为本身的重力小于所排开液体的重力,在液体里受到了不平衡力的作用,而使物体改变了原来的运动状态。
【下沉】指的是一种竖直向下的运动,如物体在液体里向下沉降。凡是在液体里下沉的物体,其本身的密度必然大于液体的密度,即ρ物>ρ液。当浮力F浮小于重力G时,物体就下沉,一直沉到容器底为止。
【浮力公式】运用阿基米德定律在解决一些实际问题时,应深入理解所运用的浮力公式F浮=ρ液gV排液和求重力公式G=ρgV。两式从字母看很相似,又有一定的联系,但两个式于是有区别的,应当注意几点:
1.求浮力实际上就是求物体所排开液体的重力。此处ρ液表示液体密度,决不是浸在液体中物体的密度;V排表示物体所排开的液体(或气体)的体积,它不一定等于物体的体积V。因为物体有漂浮、悬浮和浸没几种情况,只有当物体全部浸没在液体(或气体)中时,物体所排开的液体(或气体)的体积才等于物体本身的体积,即V排=V物。假如物体是漂浮的,那么V排就小于物体的体积V,V排<V物,这时V排+V露=V物。所以,在写浮力公式时应在F、ρ、V等字母的右下角一定用汉字注明,例如,区别开ρ液与ρ物; V物、V露与V排;G物、G液与G排的意义。
2.从公式F浮=ρ液gV排可以看出浮力的大小只跟液体的密度,物体排开这种液体的体积这两个因素有关。跟这个物体的密度、体积、形状、重力,以及这个物体在液体中是否运动等因素无关。若这个物体完全没入液体中时,它所受浮力的大小不受深度变化的影响。
3.在应用F浮=ρ液gV排液公式时,各物理量一般采用国际单位。密度ρ的单位是千克/米3,g=9.8牛顿/千克,体积V的单位是“米3”。浮力的单位是“牛顿”。
4.计算浮力的大小时,无论物体的外形是有规则的,还是不规则的;无论物体是实心的还是空心的;也无论物体在液体中的状态怎样,它所受浮力的大小都可以通过计算排开液体的重力得到。
5.阿基米德定律及其计算式,也适用于气体。因为在大气里的物体,它所排开大气的体积就等于它本身的体积,即V排=V物。因为大气的密度是不均匀的,随着高度的增加,则空气逐渐稀薄,密度减小,在计算时应考虑ρ气的变化。
【浮力测定】根据已掌握的如质量、密度、重力、体积、压力、压强、拉力等,可归纳出计算浮力的四种方式:
1.实验法之一。根据力的平衡原则,从物体在空气中的重力减去物体在液体中的重力,即得出浮力F浮=G物-G视。
2.实验法之二。根据阿基米德定律F浮=ρ液gV排液计算。
3.对于漂浮在液面或悬浮在液体中的物体,浮力等于物体的重力,即F浮=G物。
4.根据浮力产生的原因,液体对物体向上和向下的压力差就是液体对物体的浮力,即F浮=F上-F下。浮体受到的浮力等于物体的下表面受到液体向上的压力,即F浮=P·S=ρ液ghS(h为物体下表面在液面下的深度)。
【排水量】船的大小是用排水量来表示的。是指船装满货物后排开水的重力,也就是船满载后受到水的浮力。根据物体漂浮的条件,即可得出下列公式:
排水量(浮力)=船自身的重量+满载时货物的重力。
【吃水线】表示轮船没入水中的深度,在船旁用油漆画上很多水平横线,用以表示不同载重时的吃水深度。最高吃水线表示最大的安全载重量。
【浮沉子】用以演示液体浮力、气体具有可压缩性以及液体对压强的传递的仪器。它是法国科学家笛卡儿(1596—1650)所创造。它是玻璃制的小瓶体,其下端开有小孔,水可通过小孔进出瓶体。把它放入高贮水筒中,并使之浮在水面上。用薄橡皮膜把筒口蒙住并扎紧,用手按橡皮膜,简内的水和空气是在密闭的容器内。根据帕斯卡定律,当空气被压缩时,将压强传递给水,水被压入瓶体中,将瓶体中的空气压缩,这时浮沉子里进入一些水,它的重力增加,大于它受到的浮力,就向下沉。手离开橡皮膜,筒内水面上的空气体积增大,压强减小,浮沉子里面被压缩的空气把水压出来,此时浮沉子的重力小于它所受的浮力,因此它就向上浮。当手对橡皮膜施加的压力适当时,浮沉子便悬浮在水中的任意深度上。浮沉子的浮沉是在外加压强作用下,靠改变它的重力来实现的(体积不变)。潜水艇与浮沉子升降道理相同。
【潜水艇】潜水艇在水中可以自由浮沉,因此它是军事上的一种重要舰艇。它可以潜入水下航行,进行作战或侦察,是根据阿基米德原理制造的。当它潜水和上浮时是靠改变它自身的重力来实现的。潜水艇的侧面有水舱,当需要它下潜时,使水舱充水,于是艇身重力增大,潜艇就逐渐下沉。当水舱中充入适量的水时,潜艇就能在水中任何位置上停留,此时潜艇的重力等于浮力。当潜艇需要上浮时,可用压缩空气将水排出,当艇身的重力减小到小于浮力时即浮出水面。
【浮船坞】是一种可以移动并能浮沉的凹字形船舱。它不仅可用于修、造船舶,还可用于打捞沉船,运送深水船舶通过浅水的航道等。我国于1974年建成了第一艘25000吨的“黄山号”浮船坞。此船坞全长190米,高15.8米,38.5米宽,沉入水下最大深度是13.2米,具有13000吨的举力。它能抬起25000~30000吨载重量的海轮进行坞修。浮船坞的自动化和电气化程度较高,船坞的浮沉是由中央指挥台操纵,坞上设有电站(发电量可供十万人口的城镇照明用),以及机工、电工、木工等车间。
【比重计】比重计是根据阿基米德定律和物体浮在液面上平衡的条件制成的,是测定液体密度的一种仪器。它用一根密闭的玻璃管,一端粗细均匀,内壁贴有刻度纸,另一头稍膨大呈泡状,泡里装有小铅粒或水银,使玻璃管能在被检测的液体中竖直的浸入到足够的深度,并能稳定地浮在液体中,也就是当它受到任何摇动时,能自动地恢复成垂直的静止位置。当比重计浮在液体中时,其本身的重力跟它排开的液体的重力相等。于是在不同的液体中浸入不同的深度,所受到的压力不同,比重计就是利用这一关系刻度的。
液体比重计的长管子上,常标有下列数字标度……0.7、0.8、0.9、1.0、1.1、1.2、1.3……。当液体比重计在液体中沉至0.9的标度时,便能立刻知道所量度的液体密度为0.9。使用这种仪器,物体只会沉到被其所排除之液体的重量恰好等于它自身重量的那种深度为止。因此,液体比重计在比重较轻的液体里,比在较重的液体里要下沉得更深。例如,它在酒精里,就会比在掺水的酒精里下沉得更深;在纯牛奶里比在掺水的牛奶里较浅。将比重计依次插入比重渐减的各种液体里,如硫酸(1.8),水(1.0),醚(0.717)等,则其下沉的深度逐渐加深。因此较大的比重必位于标度的下部,较小的比重则位于其上部。标度本身当然先要经过校准,并且还要依照各种液体的比重来校准,或者直接依照所测定液体的特殊性质,如酒类的酒精成分,牛奶里的脂肪成分,硫酸里的纯酸成分等等来校准。
常用的比重计有两种。一种用来测量密度大于1的液体的密度,称“重表”。它的下端装的铅丸或水银多一些。这种比重计的最小刻度线是“1”,它在标度线的最高处,由上而下,顺次是、1.1、1.2、1.3……把这种比重计放在水里,它的大于1的标度线,全部在水面下。另一种用来测量密度小于1的液体的密度,称“轻表”。它的下部装的铅丸或水银少一些,这种比重计的最大标度线是“1”,这个标度线是在最低处,由下而上顺次是、0.9、0.8、0.7……把这种比重计放在水里时,它小于1的标度线全部在水面上。使用时,应注意根据液体的密度大于1还是小于1来选用此重计。目前中学课本不再讲比重单位而是讲密度单位,但在测密度时仍使用比重计,所测数值无大差异。
【气体的浮力】气体的浮力与液体同理,物体在空气中时,亦失去与物体相同体积的空气重力。故物体在空气中的重力,并非其真正的重,但因其所差甚小可忽略不计。不仅在空气中如此,物体在任何气体中,均受到气体的浮力。
【气球】若物体自身的重量小于同体积空气的重力,则在空气里就可以浮起来。气球的原理就是利用空气的浮力,将氢或氦装在大气囊内而成。在气囊的下面系一个篮子,人可坐在篮中随之而上升。气球在军事上极为重要,可用以侦察敌情或防御敌机。在气象观测上也可以将各种自记仪器系在球下,使之随球上升,可测高空的压力,密度和温度等方面的情况。
【飞艇】亦称“飞船”。飞艇是气球中的一种,贮氢气或煤气于长椭圆形或梭形的气囊中。因这些气体较空气轻,故能借空气之浮力以上升。囊下有艇,内装发动机,舵及推进器,用发动机旋转推进器,则艇前进。用舵改变方向。欲下降可将囊中气放出一些。惟气囊每遇落雷、太阳辐射热及发动机的热,容易爆破而损坏,故需装特异的避雷针,涂善于反射光的物质。艇内有铝支架者称为“硬式飞艇”,不用架者称“软式飞艇”。无论是气球还是飞艇,都是利用它们本身的重力加上所载的物体和人的重力小于气囊所排开空气重力,也就是小于它们受到空气的浮力,才能上升。由于高空的空气稀薄,空气的密度小,因此气球在上升的过程中,越升高则受到的浮力也在减小。当升到一定的高度时,即浮力等于气球的重力时,气球就不再上升了。当需要下降时,只要将囊中的气体放出一些,使气囊的体积减小,其所受的浮力减小,即可下降。
【简单机械】凡能够改变力的大小和方向的装置,统称“机械”。利用机械既可减轻体力劳动,又能提高工作效率。机械的种类繁多,而且比较复杂。根据伽利略的提示,人们曾尝试将一切机械都分解为几种简单机械,实际上这是很困难的,通常是把以下几种机械作为基础来研究。例如,杠杆、滑轮、轮轴、齿轮、斜面、螺旋、劈等。前四种简单机械是杠杆的变形,所以称为“杠杆类简单机械”。后三种是斜面的变形,故称为“斜面类简单机械”。不论使用那一类简单机械都必须遵循机械的一般规律——功的原理。
【杠杆】用刚性材料制成的形状是直的或弯曲的杆,在外力作用下能绕固定点或一定的轴线转动的一种简单机械。其上有支点(用O表示),动力(F)作用点,阻力(W)作用点,杠杆的固定转轴就是通常所说的“支点”,从转轴到动力作用线的垂直距离叫“动力臂”,从转轴到阻力作用线的垂直距离叫“阻力臂”。上述就是通常所讲的三点两臂。由于杠杆上三点的位置不同,即产生不同的受力效果。
【杠杆原理】亦称“杠杆平衡条件”。要使杠杆平衡,作用在杠杆上的两个力(动力和阻力)的大小跟它们的力臂或反比。动力×动力臂=阻力×阻力臂,用代数式表示为
F· L1=W·L2
式中,F表示动力,L1表示动力臂,W表示阻力,L2表示阻力臂。从上式可看出,欲使杠杆达到平衡,动力臂是阻力臂的几倍,动力就是阻力的几分之一。在使用杠杆时,为了省力,就应该用动力臂比阻力臂长的杠杆;如欲省距离,就应该用动力臂比阻力臂短的杠杆。因此使用杠杆可以省力,也可以省距离。但是,要想省力,就必须多移动距离;要想少移动距离,就必须多费些力。要想又省力而又少移动距离,是不可能实现的。
【动力】任何机械,不论是简单的还是复杂的,在工作时,总要受到两种力的作用:一种是推动机械的力叫作“动力”,另一种是阻碍机械运动的力叫作“阻力”。动力可以是人力,也可以是畜力、风力、电力、水力、蒸汽压力等,阻力除了我们要克服的有用阻力之外,还有一些是不可避免的无用阻力。
【作用线】通过力的作用点沿力的方向所引的直线,叫作“力的作用线”。
【动力臂】从支点到力的作用线的垂直距离叫“力臂”。从支点到动力的作用线的垂直距离L1叫作“动力臂”;从支点到阻力的作用线的垂直距离L2叫作“阻力臂”。如果把从动力点到支点的棒长距离作为动力臂,或把从阻力点到支点的棒长距离作为阻力臂,这种认识是错误的。这是因为对动力臂和阻力臂的概念认识不清所致。
【阻力臂】见动力臂条。
【转动轴】转动是常见的一种运动。当物体转动时,它的各点都做圆周运动,这些圆周的中心在同一直线上,这条直线叫做“转动轴”。门、窗、砂轮、电动机的转子等都有固定转轴,只能发生转动,而不能平动。几个力作用在物体上,它们对物体的转动作用决定于它们的力矩的代数和。若力矩的代数和等于零,物体将用原来的角速度做匀速转动或保持静止。
【三类杠杆】对杠杆的分类一般是两种方法。第一种是以支点、阻力点和动力点所处的位置来分的;另一种是按省力或费力来区分的。无论怎样来划分,总离不开省力、费力、不省力也不费力这几种情况。分别简述如下:
第一种分类法
第一类杠杆:是动力F和有用阻力W分别在支点的两边。这类杠杆
![]()
不省力也不费力。例如,剪金属片用的剪刀,刀口很短,它的机械利益远大于1。这是因为金属板很硬,刀口短,刀把长,即动力臂大于阻力臂,可以少用力。属于这种情况的杠杆还有克丝钳等。家庭裁衣剪布用的剪刀,把与刃基本是等长的,即动力臂等于阻力臂,属于不省力也不费力的类型。因为布的厚度较薄,不需太大的力,剪布要直故刀口要长些,为此用力不大,布剪的也直。属于这种类型的还有物理天平。又如理发用的剪刀,刀口很长,即动力臂小于阻力臂,它的机械利益小于1。这是因为剪发本来不需要多大的力,刀口长一些,能够剪得快一些和齐一些。
第二类杠杆:是支点和动力点分别在有用阻力点的两边。这类杠杆的动力臂大于阻力臂,其机械利益总是大于1,所以总是省力的。例如,用铡刀铡草、独轮车等都是这类杠杆。
第三类杠杆:是支点和有用阻力点分别在动力点的两边,这类杠杆的动力臂小于阻力臂,其机械利益总是小于1,所以总是费力的。例如,缝纫机的脚踏板、夹食品的竹夹子都属于这类杠杆。
第二种分类法
第一类杠杆:是省力的杠杆,即动力臂大于阻力臂。例如,羊角锤、木工钳、独轮车、汽水板子、铡刀等等。
第二类杠杆:是费力的杠杆,即动力臂小于阻力臂。如镊子、钓鱼杆、理发用的剪刀。
第三类杠杆:不省力也不费力的杠杆,即动力臂等于阻力臂。其机械利益等于1。如夭平、定滑轮等。
【机械利益】表示机械省力程度的物理量。机械虽然绝对不能省功,但可以省力。使机械作功的力称为“动力”(F),阻碍机械作功的力称为“阻力”(P)。使用机械的目的,在于使用很小的动力而与阻力平衡。所谓机械利益(A),就是机械的有用阻力(P)跟动力(F)
![]()
小于1。
机械利益>1时,省力费时,凡省力的机械,其机械利益必大于1。例如,独轮车、钳子、起子、省力的杠杆等都是省力的机械。机械利益=1时,不省力,也不费力。例如物理天乎。机械利益<1时,费力省时,例如竹夹、火钳等。机械利益是由实际测得的有用阻力和动力的大小所决定。由于机械润滑情况的不同,在克服同样的有用阻力时,亦有所不同。机械润滑得不好,无用阻力大,需要动力也大,机械利益就小些;机械润滑得好,无用阻力小,需要的动力也小,机械利益就大些。新生产出的机器需要磨合,汽车出厂要用上一段时间,目的是使其摩擦阻力减小。但机器陈旧,机件磨损,又会增加阻力。
【杠杆的应用】不同类型杠杆各具有不同的特点和用途。掌握了杠杆原理,就可根据需要有意识地选用不同类型的杠杆来使用。应明确:省力杠杆省力但要多移动距离,费力杠杆费力但省距离,等臂杠杆不省力也不省距离,又省力又省距离的杠杆是没有的。有的杠杆是否省力或省距离,不是永恒不变的。根据使用情况的不同,会由省力变为省距离。例如,用铁锹铲土,往车上装土的过程都会有所改变。铲土时支点在动力点及阻力点之间,在装土时动力点在支点与阻力点之间。为此,在使用杠杆时应注意几点:
1.解答杠杆问题时,必须根据题意画出示意图,在图上标出杠杆的支点、动力作用线和阻力作用线。同时用线段标明动力臂和阻力臂的大小,再根据杠杆平衡条件,列出方程,进行计算。
2.力臂是一个重要的概念。力臂是从支点到力的作用线的垂直距离,不要理解为力臂是从支点到力的作用点的长度。动力和阻力都是指作用在同一杠杆上的力,而不是作用在重物或其他物体上的力。
3.画杠杆示意图的方法:
(1)画出杠杆:用粗直线表示直杠杆,用变曲的粗线表示曲杠杆。
(2)在杠杆转动时找出支点,并在支点旁用箭头表示杠杆转动的方向。
(3)根据转动方向判断动力、阻力的方向。动力、阻力的作用点应画在杠杆上,可用力的示意图表示。
(4)用虚线表示力的作用线的延长线和力臂。
4.杠杆的平衡条件,适用于任意一个平衡位置上,所谓杠杆的平衡是指杠杆静止不转动或匀速转动。
【杆秤】它是测量物体质量的量度工具,是以提纽为转动轴,根据杠杆平衡原理制造的。杆秤主要由秤杆、秤砣、秤钩(或秤盘)等构成。如图1-23所示。G表示杆秤的重力,B点是它的重点,未挂重物时若将
![]()
A点即为杆秤的“定盘星”。在秤钩上加物W后,将秤砣从A点移到A'
![]()
![]()
力G相对应的刻度A'的位置。杆秤是我国劳动人民所发明并使用已久的测量工具,旧秤以斤,两为单位计量,目前以千克计量。

【力矩】又叫“转矩”,是表示力对物体作用时,使物体发生转动或改变转动状态的物理量。力矩是矢量。力矩的大小等于力与从转轴到力的作用线的垂直距离之乘积。如果物体所受的力不在垂直于转轴O的平面内,就必须把力分解成两个分力:一个分力与转轴平行;另一个分力是在转动的平面内。只有转动平面内的分力才可能改变物体的转动状态。因此,在力矩等于力跟力臂乘积的计算中,应理解力是在它的作用点的转动平面内的分力。如这一点在力的作用线上,则力矩为零。如果若干个力同时作用在一个物体上,则合力矩是所有分力矩的代数和。一个处于平衡的物体,顺时针方向力矩的和等于逆时针方向力矩的和,在国际单位制中,力矩的单位是米·牛顿。其方向用右手螺旋法则决定。在中学阶段,因为只研究有固定转轴的物体的平衡,力矩就只有两种转向。规定物体逆时针转动的力矩为正,使物体顺时针转动的力矩为负。力矩愈大,使物体转动状态发生改变的效果就愈明显。用大小相同的力推门时,力的作用点离转轴愈远,且方向垂直于门,力臂愈大,则推门愈省力。
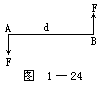
【力偶】大小相等、方向相反,但作用线不在同一直线上的两个力叫作“力偶”。用双手攻螺纹或用手旋钥匙、水龙头时,所施加的作用常是力偶。它能使物体发生转动,或改变其转动状态。汽车驾驶员双手转动转向盘时所施加的一对力就是一个力偶。力偶的转动效果决定于力偶矩的大小。力偶矩等于其中任何一个力的大小和两力作用线之间的垂直距离(力偶臂)的乘积。如图1-24所示。如果作用力F的方向跟AB垂直,AB的长度等于d,那么这个力偶的力偶矩(M)为:
M=±Fd。
式中Fd为力偶矩的大小,符号用来表示力偶的转向。规定力偶逆时针转向取“+”,反之取“-”(也可规定,力偶顺时针转向取“+”,那么力偶逆时针转向就取“-”)。应注意:力偶中力的方向不跟AB垂直时,应像力矩那样分解成垂直分量,再进行计算。力偶的转矩(即力偶矩)和所绕着转动的点无关。由于力偶的合力为零,它不能使物体产生位移,只能使物体发生转动或改变物体的转动状态。
【力偶矩】简称为“力偶的力矩”,亦称“力偶的转矩”。力偶是两个相等的平行力,它们的合力矩等于平行力中的一个力与平行力之间距离(称力偶臂)的乘积,称作“力偶矩”,力偶矩与转动轴的位置无关。力偶矩是矢量,其方向和组成力偶的两个力的方向间的关系,遵从右手螺旋法则。对于有固定轴的物体,在力偶的作用下,物体将绕固定轴转动;没有固定轴的物体,在力偶的作用下物体将绕通过质心的轴转动。
【力偶臂】力偶之两个力之间的垂直距离。见力偶条图1-24所示。
【轮轴】是固定在同一根轴上的两个半径不同的轮子构成的杠杆类简单机械。半径较大者是轮,半径较小的是轴。从形式上看是圆盘,但从实质上看起来只有它们的直径或半径起力学作用。用R表示轮半径,也就是动力臂;r表示轴半径,也就是阻力臂;O表示支点。当轮轴在作匀速转动时,动力×轮半径=阻力×轴半径,所以轮和轴的半径相差越大则越省力。上式动力用F表示,阻力用W表示,则可写成FR=Wr。
![]()
即利用轮轴可以省力。若将重物挂在轮上则变成费力的轮轴,但它可省距离。轮轴的原理也可用机械功的原理来分析。轮轴每转一周,动力功等于F×2πR,阻力功等于W×2πr。在不计无用阻力时,机械的
![]()
日常生活中常见的辘轳、绞盘、石磨、汽车的驾驶盘、手摇卷扬机等都是轮轴类机械。
【滑轮】滑轮是属于杠杆变形的一种简单机械,是可以绕中心轴转动的,周围有槽的轮子。使用时,根据需要选择。滑轮可分为定滑轮、动滑轮、滑轮组、差动滑轮等。有的省力,有的可以改变作用力的方向,但是都不能省功。
【定滑轮】滑轮的轴固定不动,它实质上是一个等臂杠杆。动力臂和阻力臂都是滑轮的半径r,根据杠杆原理Fr1=Wr2。它的机械利益为
![]()
变了动力的方向,如要把物体提到高处,本应用向上的力,如利用定滑轮,就可以改用向下的力,因而便于工作。
【动滑轮】滑轮的轴和重物一起移动的滑轮。它实质上是一个动力臂二倍于阻力臂的杠杆。根据杠杆平衡的原理Wr=F·2r,它的机械利
![]()
改变用力的方向。其方向是与物体移动的方向一致。
【滑轮组】动滑轮和定滑轮组合在一起叫“滑轮组”。因为动滑轮能够省力,定滑轮能改变力的方向,若将几个动滑轮和定滑轮搭配合并而成滑轮组,既可以改变力的大小,又能改变力的方向。普通的滑轮组是由数目相等的定滑轮和动滑轮组成的。而这些滑轮或者是上下相间地坐落在同一个轮架(或叫“轮辕”),或者是左右相邻地装在同一根轴心上。绳子的一端固定在上轮架上,即相当于系在一个固定的吊挂设备上,然后依次将绳子绕过每一个下面的动滑轮和上面的定滑轮。在绳子不受拘束的一端以F力拉之,被拉重物挂在活动的轮架上。对所有各段绳子可视为是互相平行的,当拉力与重物平衡时,则重物W必平均由每段绳子所承担。若有n个定滑轮和n个动滑轮时,
![]()
且为匀速运动时,则所需之F力的大小仍和上面一样。因此,在提升重物时才能省力。其传动比乃为F∶W=1∶2n。注意,在使用滑轮组时,不能省功,只能省力,但省力是以多耗距离(即行程)为前题的。
前边所分析的定滑轮、动滑轮以及滑轮组,都是在不计滑轮重力,滑轮与轴之间的摩擦阻力的情况下得出的结论。但在使用时,实际存在轮重和摩擦阻力,所以实际用的力要大些。
【差动滑轮】即链式升降机,是一种用于起重的滑轮组。上面是由两个直径不同装在同一个轴上的圆盘A、B组成的定滑轮。下面是一个动滑轮,用铁索与上面的定滑轮联结起来而成滑轮组。若大轮A的半径是R,小轮B的半径是r,如图1-25所示。当动力F拉链条使大轮转一周,动力F拉链条向下移动了2πR,大轮卷起链条2πR,此时小轮也转动一周,并放下链条长2πr于是动滑轮和重物W上升的高度为
![]()
由于2R大于(R-r),差动滑轮的机械利益大于1,若提高机械利益,可加大两轮的半径同时缩小两轮间的半径差。这种机械,亦称“葫芦”,有手动,也有用电来驱动的。链条是闭合的,为防止滑轮和链条间的滑动,滑轮上有齿牙与链条配合运动。

【斜面】简单机械的一种,可用于克服垂直提升重物之困难。距离比和力比都取决于倾角。如摩擦力很小,则可达到很高的效率。用F表示力,L表示斜面长,h表示斜面高,物重为G。不计无用阻力时,根据功的原理,得
FL=Gh
倾角越小,斜面越长则越省力,但费距离。
【螺旋】属于斜面一类的简单机械。例如螺旋千斤顶可将重物顶起,它是省力的机械。千斤顶是由一个阳螺旋杆在阴螺旋管里转动上升而将重物顶起。根据功的原理,在动力F作用下将螺杆旋转一周,F对螺旋做的功为F2πL。螺旋转一周,重物被举高一个螺距(即两螺纹间竖直距离),螺旋对重物做的功是Gh。依据功的原理得
![]()
很小的力,就能将重物举起。螺旋因摩擦力的缘故,效率很低。即使如此,其力比G/F仍很高,距离比由2πL/h确定。螺旋的用途一般可分紧固、传力及传动三类。
【齿轮和齿轮组】两个相互咬合的齿轮,在它们处于平衡状态时,由力矩平衡方程可得
F·r1=G·r2
式中F表示作用力,G表示物重,r1和r2分别表示大、小齿轮的半径。它们的机械利益为
![]()
![]()
(R为大齿轮半径)。
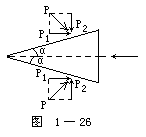
【劈】亦称“尖劈”,俗称“楔子”。它是简单机械之一,其截面是一个三角形(等腰三角形或直角三角形)。三角形的底称作劈背,其他两边叫劈刃。施力F于劈背,则作用于被劈物体上的力由劈刃分解为两部分,如图1-26所示。P是加在劈上的阻力,如果忽略劈和物体之间的摩擦力,利用力的分解法,知P与劈的斜面垂直,P的作用可分成两个分力:一个是与劈的运动方向垂直,它的大小等于P·cosα,对运动并无影响;另一个是与劈的运动方向相反的,它的大小等于P·sinα,对运动起阻碍作用。所以,当F=2P·sinα时劈才能前进,因而P与F大小之比等于劈面的长度和劈背的厚度之比,因此劈背愈薄,劈面愈长,就愈省力。劈的用途很多,可用来做切削工具,如刀、斧、刨、凿、铲等;可用它紧固物体,如鞋楦榫头,斧柄等加楔子使之涨紧;还可用来起重,如修房时换柱起梁等。
【功】是描述物体状态改变过程的物理量,能量变化的量度。功的概念来源于日常生活中的“工作”一词。在物理学中,它有特殊的涵意。当物体在恒力F的作用下,力的作用点的位移是S时,这个功就等于力跟距离的乘积。对初中学生来说,只要明确“在力的作用下,物体沿力的方向通过了一段距离,那么这个力就对物体做了功”,这是指物体在恒力作用下,沿力的方向作单向直线运动的情况,所以对功的计算可用公式W=FS。当物体在恒力作用下,作非单向直线运动,如竖直上抛运动、平抛运动、斜抛运动等等,物体受力方向和运动方向不一定是一致时,对功的理解应加深为“力对物体所做的功,等于力的大小、力的作用点的位移大小,力和位移间夹角的余弦三者之乘积”即W=FScosα。式中W表示外力F对物体所做的功,S表示物体移动的路程,α表示F与S之间的夹角。根据公式研究力对物体做功的一些情况:
1.当α=0°时,W=FS,力对物体做正功;
2.当0°<α<90°时,1>cosα>0,则力F的有效分力Fcosα和物体的运动方向一致,力F对物体做正功;
3.当α=90°时,cosα=0,则W=0,此时力F对物体不做功;
4.当180°>α>90°时,-1<cosα<0,则W<0,即W为负值。在这种情况下F对物体做负功,也可说成物体克服阻力F做功;
5.当α=180°时,则W=-FS,这时力F对物体做负功,或者说成物体克服阻力F做功。
必须注意:在研究有关“功”的问题时,应分清有没有做功,谁在做功。功是一个只有大小而没有方向的物理量,它是标量而不是矢量。至于正功和负功,不过是区别外力对物体做功还是物体克服阻力做功,或用来表示力与路程同向还是反向,并不是功有方向性。
功是力对空间的累积效应。力对物体做功,使物体发生位置或运动状态的改变,因而也就发生了机械能的改变。功即是反映在这一过程中,物体机械能改变多少的物理量。在力学中功的狭义概念仅指机械能转换的量度;而在物理学中功的广义概念指除热传递外的一切能量转换的量度。所以功也可定义为能量转换的量度。一个系统总能量的变化,常以系统对外做功的多少来量度。能量可以是机械能、电能、热能、化学能等各种形式,也可以多种形式的能量同时发生转化。功的单位和能量单位一样,在国际单位制中,都是焦耳。
计算变力做功是把运动的轨迹分成许许多多无限小的小段,在每个小段内,可以把力看作为恒力,按恒力做功的定义来计算在各个小段内所做的功,最后把各个小段的功加起来,就是变力做的功,即A=ΣFi·ΔSi,如果力和位移都是连续的,则可用积分法计算,
![]()
【功的原理】亦称“机械功的原理”。即动力对机械所做的功等于机械克服阻力所做的功。也就是说利用任何机械都不能省功。动力功W动,又称输入功或总功。阻力功W阻,包括克服有用阻力所做的W有用(又称输出功)和克服无用阻力所做的W无用(又称损失功),即W动=W阻=W有用+W无用。也可写成W输入=W输出+W损失。功的原理是机械的基本原理。要省力就要多移动距离,要少移动距离就要多用力,使用任何机械都不能省功。在机械做功过程中,只有在不存在无用阻力,机械本身作匀速运动的理想情况下,有用功才等于总功,效率为100%。事实上,必然存在无用阻力,效率一定小于100%,也就是说使用任何机械,在实际情况下总是费功的。应明确,只有在理想情况下,有用功才等于总功。
【正功】作用力的方向和力的作用点的位移方向之夹角小于90°且大于或等于0°时(即α为锐角),根据公式作用力A做正功。当力F与位移S夹角α=0°时,W=FScos0°=FS,F做最大正功;0°<α<
![]()
【负功】当作用力方向与力的作用点位移方向夹角大于90°且小于或等于180°时,这时cosα<0,根据公式功为负。力对物体作负功-A就代表受力作用的物体克服阻力作了正功A。这两种说法描述的是同一物理过程。例如,空气压缩机中空气对活塞作负功,也可以说成是活塞克服空气的压力作正功。又如,汽车紧急制动,车轮停止转动,轮胎在地面上滑动,这时摩擦力对汽车作负功,反过来也可以说汽车克服摩擦力作正功。
【功率】功跟完成这些功所用时间的比值叫做“功率”。最初定义功率为“单位时间里完成的功”,它是指做功快慢不变的情况,初中学生易于掌握。“功跟完成这些功所用时间的比值”这一定义功率,对于做功快慢不变的情况,既表示平均功率,又表示即时功率。对于做功快慢不均匀的情况,如时间取得长些,则为平均功率;时间趋于零,这一
![]()
![]()
率,只能表示机器在一段时间t内的平均功率。而由公式P=Fv计算出来的功率就有了不同的含义。若速度v代表平均速度,那么P代表平均功率,如果v代表即时速度,那么P就代表机器在某瞬时的即时功率。
公式中力是一个矢量,速度也是一个矢量,而功率却是一个标量。
![]()
方法,一为“标积”;一为“矢积”。两矢量的“标积”为一标量,其大小(к)为两矢量的大小和两矢量夹角的余弦的乘积,用公式表示为
![]()
![]()
式P=Fv中,实际上P应为 ![]() 矢量和
矢量和 ![]() 矢量的标积,即
矢量的标积,即
![]()
所以得到的功率P应为一标量。
关于公式P=Fv,中F与v成反比的关系,应明确,不能脱离具体条件,防止得出谬误的结果。因为机器的牵引力要受速度的限制,又受机器的构造、运转条件等限制,任何机器在设计制造时,已规定了它的正常功率和最大作用力。超过最大作用力范围,牵引力和速度成反比这一关系就不能适用。另一方面也不能使机器的牵引力趋近于零,而使机器的速度无限制地增加。因为任何机器在工作时要受到阻力作用,阻力还与机器运转的速度有关。即使在没有负载的情况下,机件间的摩擦阻力仍然存在。为维持机器的运转,发动机的牵引力不能小于它所受的阻力。因而它的速度也不能无限增加。因此,任何机械在有一定的最大输出功率的同时,还具有一定的最大速度和最大作用力。
功率的常用单位是瓦特(焦耳/秒),简称瓦,单位符号W。瓦特这个单位较小,技术上常用千瓦做功率的单位。过去还有尔格/秒、牛顿·米/秒、千克力·米/秒。
![]()
间t内的平均功率。当物体受恒力作用时也可表示为P=F ![]() 。式中
。式中 ![]() 表示某段时间的平均速度。平均功率随所取的时间不同而不同,因此在谈到平均功率时,一定要指出是哪一段时间内的平均功率。参阅功率条。
表示某段时间的平均速度。平均功率随所取的时间不同而不同,因此在谈到平均功率时,一定要指出是哪一段时间内的平均功率。参阅功率条。
【即时功率】即“瞬时功率”,简称功率。描述机械在某一瞬间作
![]()
![]()
![]()
物体运动即时速度的乘积。作平均速度时,P当然代表平均功率,如果作即时速度,那么P就代表机械在某瞬时的即时功率。当作匀速运动时,即时功率和平均功率相同。
【马力】功率的常用单位,它是工程技术上常用的一种计量功率的单位。是指米制马力而不是英制马力,英国、美国等一些国家采用的是英制马力。1英制马力等于550英尺·磅/秒,等于745.7瓦特。在18世纪后期,英国物理学家瓦特(1736—1819)为了测定新制造出来的蒸汽机的功率,他把马力的定义规定为在1分钟内把1000磅的重物升高33英尺的功,这就是英制马力,用字母HP表示。指的是米制的马力,它的规定完全是人为的,它取了一个非常接近英制马力的值。规定1米制马力是在1秒钟内完成75千克力·米的功。即:1米制马力=75千克力·米/秒=735瓦特。1英制马力=1.0139米制马力。米制马力没有专门的字母表示,1米制马力的值和1英制马力的值也是不同的。马力在我国法定计量单位中已废除。
【瓦特】功率的国际单位制专门名称,符号为W,为纪念英国科学家瓦特(1736—1819)而得名。每秒钟作出1焦耳的功为1瓦特,即焦耳/秒。其常用十进倍数单位和分数单位有:
1兆瓦(MW)=106瓦(W)
1千瓦(kW)=103瓦(W)
1毫瓦(mW)=10-3瓦(W)
1微瓦(μW)=10-6瓦(W)
【焦耳】英国物理学家、研究电与热。1840年,他由实验的结果发现了焦耳定律。接着以实验证明,热和功在本质上是相同的,而确立了能量不灭定律,测定了热的功当量。他和楞次各自独立地发现了电流通过导体时发生热量的定律,称为焦耳—楞次定律。焦耳是能量和功的国际制单位的专门名称,符号为J。1焦耳相当于1牛顿的力使物体在力的方向上移动1米时所做的功。其定义式为:W=FS,即1焦耳=1牛顿·米,也等于1瓦特的功率在1秒钟内所作的功(W=Pt),即1焦耳=1瓦特·秒。
![]()
【尔格】能量和功的厘米·克·秒制单位的专门名称,国际符号为erg。1尔格相当于质量为1克、速度为1厘米/秒的运动物体所具有的动能,或相当于1达因的力沿着力的方向移动1厘米所做的功。lerg=10-5J。
【达因】力的厘米·克·秒制单位的专门名称,国际符号为dyn。1达因的力相当于促使质量为1克的物体获得1厘米/秒2的加速度的力,
![]()
非法定计量单位。
【额定功率】指工厂生产的机器在正常工作时所能达到的功率。即平常所说的某机器的功率。机器的额定功率是一定的,P=Fv,所以机器产生的力和运转速度成反比。例如,汽车行驶在平坦的柏油路面时,需要的牵引力F较小,时速就可以大些;在路不平坦或上山时,需要的牵引力大,就必须改用低速行驶。
【机械能】物质机械运动的量度。机械能有两种不同的形式——动能和势能。动能,重力势能和弹性势能统称为机械能。
【能量】简称“能”,它是描述物质(或系统)运动状态的一个物理量,是物质运动的一种量度。任何物质都离不开运动,在自然界中物质的运动形式是多种多样的,相应于各种不同的运动形式,就有各种不同形式的能量。自然界中主要有机械能、热能、光能、电磁能、原子能等形式的能量。当运动形式之间相互转化时,它们的能量也随之而转换。例如,利用水位差产生的河水中冲击力推动水轮机转动,能使发电机发电,将机械能转换为电能;电流通过电热器能够发热,使电能转换为热能;电灯泡可使电能转换为光能和热能;各种内燃机,利用汽油或柴油在汽缸中燃烧的过程,将化学能转换为热能,热能再转换为机械能,推动活塞往复移动。从上述的实例,证实各种形式的能量都可相互转化,在转化过程中,一种形式的能增加了多少,必有另一种形式的能减少多少,能的总量保持不变。自然界一切过程都服从能量守恒和转换定律。物体要对外界作功,就必须消耗本身的能量或从别处得到能量的补充,因此一个物体的能量越大,它对外界就有可能作更多的功。能量是一个标量。用数学语言说,能量是物质运动状态的一个单值函数。能量的单位与功的单位一致。常用的单位是焦耳、千瓦小时等,和功的单位相同。能量和质量之间具有密切的关系。
【动能】物体由于本身运动而具有的能量,或者说,由物体运动的速度所确定的能量叫做“动能”。在一般条件下,一个作平动的物体,
![]()
增减,没有方向,而且不会小于零,所以动能是标量,而不是矢量。当物体作变速运动时,其动能是随时在变化的,所以,计算变速运动物体的动能时应明确在哪一时刻的动能。由于物体的运动速度是相对的,因此物体的动能也是相对的,它对于不同的参照物有不同的值。一个以角速度ω作转动的物体,如果它绕某一转轴的转动惯量是I,则它的转动
![]()
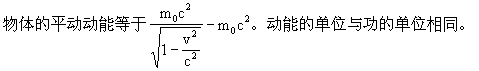
【动能定理】合外力对物体所做的功,等于物体动能的增量,这一结论叫做“动能定理”。即
![]()
式中Ek1和Ek2各表示运动物体在初状态时和末状态时所具有的动能,W合表示合外力(即外力的合力)对物体所做的功,也就等于各个外力对物体所做的总功W总。如果ΔEk>0,则表示外力对物体做正功,物体获得能量,动能增加;如果ΔEk<0,则表示外力对物体做负功,即物体对外做正功,或者说物体克服外力做功,物体必须消耗能量,它的动能减少;如果ΔEk=0,这说明外力对物体不做功,物体的动能不增加也不减少。
动能定理是力学中一条重要规律,它是根据牛顿运动定律推导出来
![]()
定理中的FScosα代表作用在运动质点上的合外力的功。从动能定理深入领会“功”和“动能”两个概念之间的区别和联系。动能是反映物体本身运动状态的物理量,物体的运动状态一定,能量也就唯一确定了,故能量是“状态量”,而功并不决定于物体的运动状态,而是和物体运动状态的变化过程,即能量变化的过程相对应的,所以功是“过程量”。功只能量度物体运动状态发生变化时,它的能量变化了多少,而不能量废物体在一定运动状态下所具有的能量,有的书上把动能定理称之为动能原理。对原理、定理区分不严格,本辞条按课本教材要求,称“动能定理”。此定理体现了功和动能之间的联系。称为定理的原因是因为它是从牛顿定律,经数学严格推导出来的,并不能扩大其应用范围。由于动能定理不涉及物体运动过程中的加速度和时间,不论物体运动的路径如何,因而在只涉及位置变化与速度的力学问题中,应用动能定理比直接运用牛顿第二定律要简单。
【势能】亦称“位能”。由相互作用的物体之间的相对位置,或由物体内部各部分之间的相对位置所确定的能叫做“势能”。按作用性质的不同,可以分为引力势能、弹性势能、电势能和核势能等。力学中势能有引力势能、重力势能和弹力势能。势能不是属于单独物体所具有的,而是相互作用的物体所共有。在相互作用力是“耗散力”(如摩擦力)时,设物体由A点(假设它是势能零点)移到B点克服它做功为W,当物体由B点回到A点时,它并不能对物体做功,故不能说由于耗散力存在使物体具有了势能。与此相反,如果上述过程是在保守力作用下进行的,那么物体从B回到A时,保守力对物体做的功正好等于W,这是因为保守力所做的功才只与物体的初始和最终的相对位置有关。如果物体不受其他力的作用那么这个功W就使物体得到同样多的动能。故我们说物体在B点有势能W。总之势能的大小由体系内各物体之间保守力所作的功来量度。势能是属于物体系共有的能量,通常说一个物体的势能,实际上是一种简略的说法。势能是一个相对量。选择不同的势能零点,势能的数值一般是不同的。
【重力势能】由于地球和物体间的相互作用(重力)物体所具有的能量叫做“重力势能”。物体由于被举高才具有重力势能,而物体在举高过程中是在克服重力做功。因此,重力势能跟克服重力做功有密切关系。用Ep表示重力势能,则
Ep=mgh。
从上式看,物体的重力势能等于它的重力和高度的乘积,或等于物体的质量、重力加速度、高度三者的乘积。物体的质量越大,高度越大,它的重力势能就越大。重力势能是相对的,同一物体的重力势能的大小决定于零势能位置的选择。零势面以下的物体,重力势能为负值。物体的重力势能属于物体与地所共同具有的。重力对物体做的功等于物体重力势能的增量的负值。即重力所做的功只跟初末位置有关,而跟物体运动的路径无关。
【弹性势能】物体由于发生弹性形变,各部分之间存在着弹性力的相互作用而具有的势能叫做“弹性势能”。在工程中又称“弹性变形能”。例如,被压缩的气体、拉弯了的弓、卷紧了的发条、拉长或压缩了的弹簧都具有弹性势能,被压缩或伸长的弹簧具有的弹性势能,等于弹簧的倔强系数K与弹簧的压缩量或伸长量x的平方乘积的一半,
![]()
弹力势能的单位与功的单位是一致的。确定弹力势能的大小需选取零势能的状态,一般选取弹簧未发生任何形变,而处于自由状态的情况下其弹力势能为零。弹力对物体做功等于弹力势能增量的负值。即弹力所做的功只与弹簧在起始状态和终了状态的伸长量有关,而与弹簧形变过程无关。弹性势能是以弹力的存在为前提,所以弹性势能是发生弹性形变,各部分之间有弹性力作用的物体所具有的。如果两物体相互作用都发生形变,那么每一物体都有弹性势能,总弹性势能为二者之和。
【引力势能】物体系的各物体之间由于万有引力相互作用而具有的势能叫做“引力势能”。例如地球周围各物体和地球之间有引力作用,因此这个物体具有引力势能。在物体远离地面的情况下,通常将距地心无限远处定为零势能状态,这时引力势能公式应为
![]()
该式又叫引力势能公式,式中G是万有引力常数,M、m分别为地球和物体的质量,r是物体与地心之间的距离。
【机械能守恒定律】合外力(不包括万有引力、重力和弹性力)对物体没有做功或所做的功为零时,任何物体在势能和动能相互转化过程中,物体的总机械能(即势能和动能的总和)保持恒定不变,这一结论就叫做“机械能的转化和守恒定律”。是自然界最普遍定律——能量的转化和守恒定律的一种特殊形式,是力学中重要定律之一。机械能守恒定律只适用于机械能与非机械能没有发生转化的系统,通常将这样的系统称为机械能守恒系统。机械能守恒定律只涉及初始状态和终了状态的机械能,不涉及转换过程。因此,如果不要求去了解过程的具体情况的话,用机械能守恒定律来分析某些力学过程,比用其他方法简便。
【功能原理】合外力(不包括万有引力、重力和弹性力)对物体所做的功等于物体机械能的增量,这个结论就叫做“功能原理”。其表达式为
W合=E2-E1=ΔE。
式中E1和E2各表示物体在初状态和末状态时的机械能,W合表示合外力(不包括重力和弹性力)对物体所做的功。从式中可知:当机械能增加时,即E2>E1,则ΔE>0,合外力对物体做正功;当机械能减少时,即E2<E1,则ΔE<0,合外力对物体做负功;机械能不变时,即E2=E1,则ΔE=0,合外力对物体不做功。从上述分析知:能是表达物体运动状态的物理量,用做功的多少可以量度能量的变化量。功和能都是标量,它们的单位相同,但却是两个本质不同的物理量。能是用来反映物体的运动状态的物理量。处于一定的运动状态的物体就具有一定的能量。而作功的过程是物体在力的作用下,位置变化的过程,也就是能量从一个物体传递给另一个物体的过程。因此,功是用来反映某一过程中物体间能量传递了多少的物理量。
【冲量】作用在物体上的力和力的作用时间的乘积,叫做该力对这物体的“冲量”。冲量的作用是使受力物体的动量发生变化。冲量的数学公式为I=Ft。冲量是矢量,它的方向跟作用力的方向相同。因为冲量是力对时间的累积效应,它是一个过程物理量。只要有力,而且力作用了一段时间,不论力的大小,作用时间的长短,总有力的冲量。在国际单位制中,力的冲量的单位为牛顿·秒(过去常用的单位还有达因·秒)。
【动量】用物体的质量(m)和它的速度(v)的乘积来描述物体运动状态的物理量叫做“动量(P)”。用公式表示为P=mv。它是一个矢量,跟速度的方向相同。其大小等于物体的质量跟速度的乘积。一物体的机械运动转移为另一物体的机械运动,反映为物体之间动量的传递。因而动量是物体运动的一种量度。动量的单位是千克·米/秒。从量纲上看它跟冲量的单位是一致的。由于速度还具有瞬时性和相对性,所以,动量也还具有瞬时性和相对性。
【动量定理】物体的动量的增量,等于相应时间间隔内物体所受合外力的冲量。它表明具有动量的物体受合外力作用,经过一段时间速度将发生变化,因而动量也发生变化。此时,物体所受的合外力的冲量等于它的动量的变化。数学表达式是:ΣI=P2-P1=ΔP。其中ΣI表示各外力冲量的矢量和,即Σ(F·t),它等于合外力的冲量。P1、P2各表示物体在始、末状态时的动量。冲量和动量都是矢量。冲量的方向是动量增量的方向。冲量是对力而言,动量是对物体而言的。只能说“某力的冲量”、“某物体的动量”,而不能讲“某力的动量”、“某物体的冲量”。国际单位制中,力的冲量的单位为牛顿·秒,物体动量的单位为千克·米/秒。它们具有相同的量纲。动量单位和冲量单位等同,即1牛顿·秒=1千克·米/秒,(1达因·秒=1克·厘米/秒)
运用动量定理可以求解力、质量、速度三方面问题。解决具体问题的思路和方法是;明确物理过程;确定研究对象;进行受力分析;确定作用前的动量和作用后的动量;建立坐标系或规定正方向,根据动量定理列出方程;求解。
【动量守恒定律】物体系不受外力作用,或所受外力的合力为零,则系统的总动量守恒。这一结论叫“动量守恒定律”。其数学表达式为:m1v1+m2v2=m1v1'+m2v2'=恒量。式中的m1、m2分别为两个物体的质量,v1和v2分别为它们原来的速度,v1'和v2'分别为它们相互作用后的速度,等号左边是两物体原来的总动量,右边是它们相互作用后的总动量。该定律是指相互作用的物体的总动量是守恒的。但在作用过程中,动量从一个物体传递给其他物体,即每一物体的动量并不守恒。运用此定律时还应注意守恒条件:要求系统不受外力或所受外力的合力为零。但当外力远小于内力时亦可运用。如外力不为零,但在某一方向上的外力为零,则可在这一方向运用该定律。从大到星系的宏观系统,小到基本粒子的微观系统,无论系统内各物体之间相互作用是什么力,只要能满足守恒条件,都可运用动量守恒定律。所以它是自然界最重要最普遍的规律之一。
【麦克斯韦滚摆】简称“滚摆”。它是演示机械能转换的仪器。在演示前应调绳使摆轮处于水平状态。演示时用手捻动摆轴,使滚摆上升,同时悬线就缠在轴上。滚摆升到顶点的时候,具有一定的势能。若将摆松开,它就旋转下降,势能随着滚摆的下降而逐渐减少;可是它越转越快,表示动能在逐渐地增加,当悬线完全伸开,滚摆不再下降时,由于滚摆的继续旋转,它又开始绕着悬线上升。在上升过程中,动能逐渐减少,而势能则逐渐增加。上升到跟上一回差不多的高度,然后再下降,再上升,假如没有阻力(例如空气阻力、绳子与轴的摩擦力等),滚摆每次上升的高度相同。即滚摆的势能和动能在转换过程中总量保持不变。
【碰撞】相对运动着的物体靠近时在极短时间内运动状态发生显著变化的过程叫做“碰撞”。碰撞是一种常见的现象。碰撞的一个特点是冲力很大,在碰撞过程中,可以不考虑外力对碰撞质点运动的影响,往往将外力忽略不计,而用动量守恒定律处理质点系的运动问题。碰撞过程的另一特点是时间短,而运动状态在碰撞前后的变化又非常显著。因此,很容易分清哪是在碰撞前,哪是在碰撞后,哪是碰撞开始,哪是碰撞过程的结束。这为运用动量守恒定律,创造了有利条件。
物体(或质点)之间相互作用实际是交换能量和动量的过程。碰撞不仅指物体相互接触时的冲击过程,微观粒子间非接触的相互作用而干扰它们的运动状态的过程也叫碰撞。若以物体间碰撞的形式区分,可分为对心碰撞(正碰)、非对心碰撞(斜碰)。如以物体碰撞前后两物体的总动能是否变化来区分,可分为弹性碰撞,非弹性碰撞,而完全非弹性碰撞则是非弹性碰撞的特例。
各类碰撞都遵守动量守恒定律和能量守恒定律,即物体系内各物体碰撞前的总动量和总能量分别等于碰撞后的总动量和总能量。不过在非弹性碰撞中,有一部分动能转变为其他形式的能量,因此,动能就不守恒了。碰撞的过程一般伴随着两种力学过程:机械运动的传递;机械运动和其他运动形式的转化。
【正碰】亦称“对心碰撞”。物体在相互作用前后都沿着同一直线(即沿着两球球心连线)运动的碰撞。在碰撞时,相互作用力沿着最初运动所在的直线,因此,碰撞后仍将沿着这条直线运动。研究正碰时,可如上述沿两小球球心的联线作x轴。碰撞前后的速度就在x轴上,根据动量守恒定律则可判断两小球碰撞前后的总动能是否守恒,从而将碰撞分为弹性碰撞和非弹性碰撞。在原子或原子核的碰撞中,把碰撞后入射粒子和靶沿同方向或相反方向运动的碰撞或者靶在碰撞后沿入射方向运动的碰撞亦称为正碰。
【斜碰】亦称“非对心碰撞”。两球在碰撞前的相对速度不沿两球球心连线的碰撞叫“斜碰”。研究斜碰问题时,运用正交分解法较为方便。斜碰也可分为弹性碰撞、非弹性碰撞两类。
【弹性碰撞】参加碰撞的所有粒子或物体的总动能在碰撞前或在碰撞后彼此相等的碰撞,叫做“弹性碰撞”。动量和动能同时守恒的碰撞也称“完全弹性碰撞”。设m1、m2代表两个物体的质量,u1、u2表示碰撞前两物体的速度,v1、v2表示碰撞后两物体的速度。以下只讨论两物体的对心碰撞,即u1、u2、v1、v2都沿同一直线。弹性碰撞的过程遵守动能守恒定律和动量守恒定律,即
![]()
m1u1+m2u2=m1v1+m2v2。
如两物体的质量和碰撞前的速度已知,则碰撞后的速度
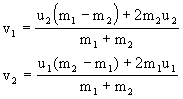
两式相减得v1-v2=u2-u1。
上式v1-v2是两物体碰撞后的相对速度(分离速度),u2-u1是它们碰撞前的相对速度。对于弹性碰撞,两物体碰撞前后的相对速度大小不变,但方向相反。完全弹性碰撞的一个基本条件:两物体相碰时,它们之间的相互作用力是弹性力,不存在耗散力。而且碰撞过程可分为两个理想的阶段,把两个理想阶段也定为完全弹性碰撞的条件是因为它能保证,碰后,每个小球都不具有内部发生的弹性振动能。压缩阶段,由开始发生变形至两物体相对速度为零,两物体克服弹性力作功,一部分动能转化为弹性势能;在恢复阶段,弹性力作功,两接触物体形变完全消失,弹性势能又全部转化为两球的动能,而以不同速度分离。微观粒子的弹性碰撞,相碰撞的粒子速度的大小和方向都发生改变,但它们的内部状态没有变化,如低能电子在分子上的散射。
【非弹性碰撞】碰撞前后物体系的总动能不守恒(但总能量仍是守恒的),碰撞过程有一部分机械能转换为其他形式的能量,称为非弹性碰撞。此过程中,碰撞体的内部状态发生变化,如物体变热、变形(不能恢复)或破裂、原子受到激发、粒子的种类或性质发生改变等。
【完全非弹性碰撞】它是非弹性碰撞中的特例。这种碰撞,当两物体碰撞后粘合为一体,以同一速度v运动,即v1=v2=v,这样的碰撞叫“完全非弹性碰撞”,这时碰撞的系统只遵守动量守恒定律,即
(m1+m2)v=m1v1+m2v2,
![]()
如果物体碰撞后,各自具有不同的速度,但系统的总动能减小,这种碰撞叫“非完全弹性碰撞”。0<e<l,即分离速度小于接近速度。对于完全非弹性碰撞,e=0,即分离速度为零,两物体粘合在一起活动。
【非完全弹性碰撞】见“完全非弹性碰撞”条。
【反冲运动】枪或火箭等系统由于发射子弹或喷射气体而发生的枪身或火箭本身沿子弹或气体速度的相反方向运动的现象,谓之反冲运动。可通过动量守恒定律加深对射击和喷气等反冲运动特点的理解。在中学教学中常涉及三种不同形式的反冲运动。1.步枪的后座。处理这一问题选择子弹与枪身这一质点系为研究的对象。首先判断从击发开始到子弹离开枪管为止,这段时间是否守恒。由于作用于枪身的爆发力(内力)比肩窝的抵抗力(外力)大得多,后者对枪身运动的影响可忽略不计。所以,在发射子弹的过程中,可应用动量守恒定律近似求解。2.炮身以仰角α发射炮弹问题。炮弹向斜上方飞出后,炮身除沿水平方向后退外,还要朝下运动。地面对炮身则产生极大的竖直向上的弹力,阻碍炮身下沉,这一竖直向上的巨大弹力属于外力。质点系所受的合外力不等于零,因此动量不守恒。但是,合外力在水平方向上的分量为零(炮身运动的摩擦力与爆炸力相比,可忽略不计),所以质点系的动量在该方向上的分量是守恒的。这就是沿某一方向的动量守恒问题。3.喷气火箭的飞行。这类反冲运动的物体,在运动中不断地释放某些气体(如气体)而运动,或在运动中不断地俘获另外一些物体而共同运动,这属于可变质量物体运动的问题。在处理这类问题时应按齐奥尔科夫斯基公式,不能死套动量守恒定律。
【机械效率(力学)】在同一时间内,机械输出功(有用功)与输入功(动力功)之比,叫做“机械效率”。任何机械在正常运转时,动力对机械所做的功,总有一部分消耗在克服摩擦和机件阻力上,这是不可避免的。因此,机械对外所做的功总小于动力对机械所做的功。动力对机械所做的功称为输入功,机械对外所做的功称为输出功。机械效率总小于1,在实用上,对于各种机器和传动设备等,机械效率指输出功率跟输入功率的百分比。实用机械效率高低不一致,效率高的多是精细、轻巧而简单的机械,效率低的都是粗糙、复杂、笨重的机器。
【内力】研究对象内部各部分之间的相互作用力称为“内力”。它不能改变系统的运动状态。例如,汽车的制动是依靠制动器的闸瓦和车轮的相互作用力来使汽车的车轮停止旋转,这种力对汽车来说只是内力,它只能使车轮停止转动,但不能使整个汽车停下来。
【外力】研究对象受到研究对象以外的物体的作用。外力改变研究对象整体的运动状态。例如,车轮由于受内力作用停止旋转,但不能使整个汽车停下来,制动的作用只不过是使车轮停止旋转,车轮和地面之间由滚动摩擦变成滑动摩擦,由于受到滑动摩擦力的作用,汽车才能迅速地停止下来。
系统的选择往往是依解决问题的方便而定,所以在同一个问题中,内力与外力又不是绝对不变的。例如,马拉车在地面上行驶,如果将马和车看成一个系统,那么马和车之间相互作用力(马对车的作用力与车对马的反作用力)就是内力;而地面给予马和车的摩擦力就是外力,如果将车当作一个系统,此时马对车的拉力就不再是内力而是外力了。
【力系】作用于物体上的一群力称“力系”。
【力场】若质点所受作用力是它在空间所处位置的函数,即在空间的每一点处都有一确定的力矢量与之对应,则称这部分空间为“力场”。例如,物体周围的万有引力场,电荷周围的静电场都是力场。
【汇交力系】力系中的各力的作用线都汇交于一点的力系,称“汇交力系”。又称共点力系。
【力线】力线是一种形象地描述力场分布而虚拟的曲线,是假想的线,实际上并不存在。它是用以表示力场强度和方向的线族,力线的密度代表场强,力线越密,场强越大。
【力程】力场作用的有效范围称为“力程”。按力程的大小,又可分为两大类:其一是短程力,即力的作用范围很小,影响力随距离的增加而急速减小。如核子间的核力,在10-13厘米的距离内,作用力很强,超过该距离后即可忽略;其二是长程力,它是随距离的增加而缓慢减少。如静电力,万有引力等平方反比力都是。
【场】在物理学中“场”是物质存在的基本形态之一。这种形式的主要特征在于它的质量和能量是弥散于空间的。根据近代物理学的观点,物质存在的基本形态可分为两种,即场和实物。由具有静止质量的基本粒子所组成的物质叫做实物。
人们对场的认识是有一段历史过程的,首先通过物体间的非接触相互作用,如物体间的万有引力作用,带电体间的静电力作用以及磁铁间的磁力作用等,逐渐认识到了场的存在。在相当长的一段时期内,曾有一种观点认为,物体间的非接触作用,是一种既不需要时间,也不需要中间媒介传递的瞬时超距作用。英国物理学家法拉第反对这种观点,并于1837年引入了场的概念。他认为那些非接触作用的发生,都必须通过某种中间媒质的传递才能实现。而这种传递相互作用的媒质就是场。它分布在整个空间或部分空间。随着科学的发展,人们逐步认识到了场的物质性,场和实物一样具有能量、动量和质量等物质的基本属性。场与实物在一定的条件下可以相互转化,例如,具有一定能量的光子可以转化为一个电子和一个正电子;同样,电子与正电子相碰可以转化为一对光子。场与基本粒子是紧密相联的,任何实物粒子都不可能脱离有关的场而单独存在,场与实物之间不存在绝对的界限。
在数学中场是一种抽象的概念,把分布在空间某一区域内的物理量或数学函数称为场,它不一定是物质存在的形式,而是为了研究方便起见,才引入场的概念。如果所研究的物理量或数学函数在空间不同的点仅有数量上的区别,其相应的场称标量场。例如温度或电势分布的场都是标量场;如果它们不仅有数量上的差异,而且还有方向上的区别,则其相应的场叫做矢量场。例如,电场强度、磁感应强度,速度及重力分布的场,都是矢量场;不随时间变化的场称“稳恒场”;随时间变化的则称“可变场”。
【保守力】大小和方向完全由物体间相对位置确定的,且做功多少只由始末位置所决定.而跟路径无关的力叫做“保守力”。保守力对物体做功的多少取决于物体始末位置,如果在该力作用下,物体的运动沿闭合路线绕行一周回到了起始位置,则所做的功为零。万有引力(包括重力)、弹力等属于保守力。物体系确定后保守力和物体的运动状况无关,其大小和方向由相互作用物体的相对位置所确定。例如,物体确定后,重力的大小决定于它离开地面的高度,方向竖直向下,而和物体以什么样的速度运动无关,和物体运动速度的大小和方向如何变化无关。保守力和物体系的势能有着极为密切的联系。保守力做正功,则物体系的势能减少;反之,则物体系的势能增加。而且相对两个位置之间,功能一定,势能差一定。所以物体间存在保守力是物体系具有势能的条件。系统的各物体在只受保守力作用的情况下,其机械能守恒。保守力的功和势能的变化的关系为: W保=EP1-EP2。这里的EP2和EP1表示终点和起点的势能。当W保>0时,保守力作正功, EP1-EP2>0,物体系统的势能要减少;当W保<0时,保守力作负功,EP1-EP2<0,物体系统的势能就要增加。保守力的功决定于物体系势能的变化量,在实际问题中涉及到的只有两个状态的势能差,而不是某一状态势能的绝对值。
【非保守力】亦称“耗散力”。做功多少和物体运动路径有关的力叫非保守力。非保守力做功就不能由物体的始末位置决定,而和物体的运动路径有关。例如,人推车是克服摩擦力做功,摩擦力是非保守力,人推车对车做的功并不与车向哪个方向运动有关。又如,空气对运动物体的阻力,其方向随着物体运动的方向改变而改变,它的大小随物体运动速度增大而增加。非保守力不像保守力,对于两个位置之间,力对物体做功没有确定的值,从而相应的两个位置之间没有一定的能量差。所以非保守力和物体系的势能没有联系。物体在有非保守力作用时,其动能与势能之和(机械能)不再守恒。质点运动时做负功的非保守力也称为耗散力。除空气阻力外,爆炸力,内燃机气缸中气体对活塞的推力都是耗散力。耗散力之所以命名为“耗散”,是由于这种力所做的功一般是跟机械运动转化为非机械运动(如热运动)紧密联系在一起。
【力的正交分解法】在处理力的合成和分解问题时,我们常把力沿两个互相垂直的方向分解,这种方法叫做力的正交分解法。这是一种很有用的办法,在运用时要注意以下几点:
1.力是矢量,
![]() 在x轴和y轴上的分矢量
在x轴和y轴上的分矢量 ![]() x和
x和 ![]() y是矢量,分量为正值表示分矢量的方向跟坐标轴的方向相同,分量为负值表示分矢量的方向跟坐标轴的方向相反。
y是矢量,分量为正值表示分矢量的方向跟坐标轴的方向相同,分量为负值表示分矢量的方向跟坐标轴的方向相反。
2.确定矢量正交分量的坐标轴,不一定是取竖直方向和水平方向。例如,分析物体在斜面上的受力情况,一般选取x轴与斜面平行,y轴与斜面垂直。坐标轴的选取是以使问题的分析简化为原则。通常选取坐标轴的方法是:选取一条坐标轴与物体运动的加速度的方向相同(包括处理物体在斜面上运动的问题),以求使物体沿另一条坐标轴的加速度为零,这样就可得到外力在该坐标轴上的分量之和为零,从而给解题带来方便。
【速度的解析表示法】将速度矢量沿直角坐标轴分解叫“力的正交分解法”。又称“速度的解析表示法”。经常使用的运动分解方法有两种,一种是矢量加减的几何方法,即三角形(或平行四边形)法则以及在此基础上的多边形矢量相加(减)法则,另一种就是将速度矢量沿直角坐标轴分解,叫做速度的解析表示法。在中学课本中没有专门讨论力的正交分解法,但在某些问题中实际上已用到了正交分解法。譬如,把放在斜面上的物体所受的重力,分解为垂直于斜面和平行于斜面的两个分力,并讨论了这两个分力与斜面对物体的正压力和摩擦力的关系,这就是力的正交分解法。

这里,仅以速度矢量v在平面直角坐标系中的情形为例如图1-27所示。由坐标轴原点画v,设v与x轴成θ角,将v沿x轴和y轴的方向分解为两个分矢量vx和vy,则这两个分矢量的大小和方向,可用v在两个坐标轴上的投影来表示:
vx=vcosθ
vx和vy分别叫做速度矢量v的x轴和y轴上的分量,其大小分别表示vx和vy的大小,正负号则表示与坐标轴同向或反向。正值表示与轴的正向相同。写成矢量式,则为:
v=vxi+vyj
式中i,j为x与y轴方向的单位矢量,若已知vx,vy两个分量,则v的大小和方向可由下式求得:

应用解析法(或称正交分解法),较为方便。
【正功和负功的物理实质】
对功的计算式W=FScosα的讨论:
当0°≤α<90°时,FS≥W>0。表明:力和物体的位移方向相同或两者的夹角小于90°。W>0,作用力对运动的物体做正功。
当α=90°时,W=0。表明:力和物体的位移方向相互垂直,力对物体不做功。
当90°<α≤180°时,0>W≥-FS。表明:力和物体的位移方向大于90°,小于180°或等于180°。W<0,力对物体做负功,或者说运动物体克服阻力而做功(说了“克服”或反抗,就不能说克服阻力做负功)。力总是成对发生的,当物体A以一个力作用于物体B,物体B必然同时给予物体A一个反作用力,两者大小相等、方向相反。因此除了场力(如重力、电场力等)做功情况以外,任何两个系统之间的接触力形成做功过程时,总是正功和负功同时发生的。甲对乙做正功的过程,也是乙对甲做负功的过程。任何一个做功过程,既可以从做正功的一方来表述,也可以从做负功的一方来表述。习惯用语常将“正”字省略,而且只从正功一方来表述。“谁做了功”指的是“谁做了正功”。我们表述时,必须指明是“谁对谁做功、是什么力对什么物体做功”。这里还应注意两个问题:
1.功是标量,只有量值,没有方向。功的正、负并不表示功的方向,而且功的正、负也不是数量上的正与负,不能说正功与负功方向相反,正功和负功是借以区分谁对谁做功的标志。表示两种相反的做功效果。
2.动力总是对物体做正功,阻力总是对物体做负功,一般情况下容易理解,但遇到摩擦力做功时,可能会认为摩擦力总是做负功。这是将摩擦力和阻力等同看待的结果。其实摩擦力可能做负功,也可能做正功,当摩擦力对物体的运动起着推动作用时,它就做正功。
【势】或叫“位”。在保守场里,把一个单位质点(如重力场中的单位质量,静电场中的单位正电荷)从场中的某一点A移到参考点,场力所作的功是一个定值。也就是说,在保守场中,单位质点在A点与参考点的势能之差是一定的,人们把这个势能差定义为保守场中A点的“势”。势是保守场的位置的单值函数,与质点的存在与否无关。只有在保守场中才能引入势的概念。参考点的选定是可以任意的。例如,对于静电场参考点常选在无限远处,也可以把地球或其他大的导体选作参考点。对于重力场则把地面作为参考点。摩擦力所作的功不仅与运动质点的初、终位置有关,而且与它所通过的路径有关,所以摩擦力是非保守力。运动电荷在磁场中所受到的磁力也是非保守力。在非保守场中不存在势能,也不能引入势的概念。
【气垫导轨】气垫导轨是一种摩擦阻力很小的力学实验仪器,用来测定速度、加速度、验证牛顿第二定律和动量守恒定律,研究碰撞、简谐振动、受迫振动、阻尼振动等等。气垫导轨是利用导轨表面小孔中喷出的压缩空气,使导轨表面和滑块(即作运动的物体)之间形成一层很薄的空气膜(即所谓“气垫”)而将滑块托起。这样,滑块在导轨表面上运动时就不存在接触摩擦力,仅仅有小得多的空气阻力,滑块的运动可近似地看成是无摩擦运动。由于气垫导轨极大地减少了以往力学实验中难于克服的摩擦力的影响,因而可以获得比较精确的实验数据,大大提高实验效果。
【机械振动】物体在某一位置附近来回往复地运动,称为“机械振动”。例如,弹簧振子、摆轮、音叉、琴弦以及蒸汽机活塞的往复运动等等。凡有摇摆、晃动、打击、发声的地方都存在机械振动。振动是自然界最常见的一种运动形式,波动是振动的传播过程。振动远不止于机械运动范围,热运动、电磁运动中相应物理量的往复变化也是一种振动。产生振动的必要条件之一是物体离开平衡位置就会受到回复力的作用;另一条件是阻力要足够小。当然物体只有惯性,而物体的惯性使物体经过平衡位置时不会立即静止下来。每经过一定时间后,振动体总是回复到原来的状态(或位置)的振动称为周期性振动。不具有上述周期性规律的振动称为非周期性振动。
【回复力】能够使振动物体回到平衡位置的力称作“回复力”。每当振动物体离开平衡位置就会受到回复力的作用。它跟向心力的情况类似,回复力是根据力的效果而命名的,而不是根据力的性质命名的。它可能是重力、强力等各种性质的力,也可能是它们的分力或合力。例如单摆中,回复力是重力的切向分量;弹簧振子中,回复力是弹簧形变后产生的弹力。
【振幅】振幅是用来表示振动强弱的物理量,振动物体离开平衡位置的最大距离,叫做振动的“振幅”,通常用符号A表示。简谐振动的振幅是不变的。强迫振动的稳定阶段振幅也是一个常数。阻尼振动的振幅逐渐减小,振幅是可变化的。
有的书上说:“物体离开平衡位置的最大位移,称作振幅”。应明确振幅与位移是有区别的。因为位移是矢量,在坐标系确定之后,位移是有正负之分的。在中学物理教学中,振幅本身只表示“振动的幅度”。如振动的强弱不变,振动的振幅就是一个不变的量。振幅的单位是米或厘米。
【周期】对于任何往复循环的物理过程,都用周期表示振动的快慢。当物体作往复运动时完成一次全振动所需要的时间称为物体振动的“周期”,简称周,用T表示。周期的单位是秒。振动的显著特点是重复性,即周期性。所谓周期性,就是振动物体的位移、速度、加速度经过一定时间之后又重复地回到原来的数值,即开始的状态。例如,位移x在时
![]()
就是振动的周期。周期这个物理量是物体运动周期性的描述。简谐振动是严格的周期性运动,它的周期是一个常数。有些振动(如阻尼振动)的周期是在不断相对缓慢地变化。严格地说,这种往复运动已不再是周期性的,但周期这个物理量仍然可以反映这种运动的往复情况。
【频率】在1秒钟内,物体完成全振动的次数叫“频率”。通常用符号f表示频率。在国际单位制中,频率的单位是赫兹(Hz),简称赫。像周期一样,频率既可以表示作振动或其他周期性运动的物体每秒钟完成周期性运动的次数,又可以表示某些物理量每秒钟完成周期性变化的次数。频率等于周期T的倒数,即
![]()
【弹簧振子】一种简谐振子。它的典型结构是由一个一端固定,质量可以忽略的轻弹簧和连在它另一端(自由端)的一个带孔而不易变形的小球,并将球穿在一根光滑的水平杆上组成,这样的,以及与此类似的系统称为弹簧振子。如图1-28所示,当小球处于O点时,所受外力的合力为零,弹簧没有形变,小球不受力,这点就是平衡位置。将小球从平衡位置O向右拉到B,然后释放,小球将沿杆左右振动起来,当小球在振动过程中,它的重力和杆的支持力始终平衡。杆又很光滑,对小球的运动又没有阻力(些小阻力可略而不计),对振动起作用的只是弹簧作用在小球上的弹力。当小球受外力作用被拉到O点的右侧B点时,对平衡位置的位移方向向右,则弹力方向却向左;当小球运动到O点左侧时,位移方向向左,而弹力方向却向右,可见这个弹力的方向总是跟小球对平衡位置的位移方向相反,指向平衡位置。显然这个弹力就是迫使小球振动的回复力。由胡克定律知弹簧提供的回复力F的大小跟小球对平衡位置的位移x成正比,这一关系式为
F=-Kx
式中K是弹簧的倔强系数,负号表示回复力与位移方向相反。弹簧振子的振动是简谐振动。它是一种理想化的模型。
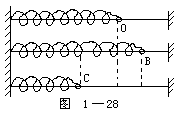
【振动】振动是一种很常见的运动形式。在力学中,指一个物体在某一位置附近作周期性的往复运动,常叫机械振动,也称振荡。见机械振动条。
一个物理量在某一恒定值附近往复变化的过程也称振动,如交流电电压、电流随时间的变化。
【简谐振动】物体在受到大小跟位移成正比,而方向恒相反的合外力作用下的运动,叫做“简谐振动”。见弹簧振子条。弹簧振子所作的运动是简谐振动。由于弹簧振子的回复力F与位移x成正比而方向相反,它们之间的关系式用F=-Kx表示。又弹簧振子的加速度a也与位移x成正比而方向相反。它们之间的关系,根据牛顿第二
![]()
式中负号表示加速度与位移方向相反。所以也可以说,凡是回复力满足
![]()
度定义的。若从运动学角度,可定义为“质点离开平衡位置的位移x随时间t而变化的规律,能遵从余弦函数(或正弦函数)的振动称为简谐振动。即x=Acos(ωt+α)。上述两种说法是对简谐振动最常用的两种定义。其实质是一样的。
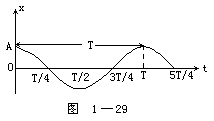
通过上述公式x=Acos(ωt+α),明显说明,作简谐振动物体的位移x随时间t的变化规律是遵从余弦函数(或正弦函数)的,如将x随t变化的关系,用图1-29所示的曲线形象地表示出来(横坐标为t,纵坐标为位移x),就是用振动图线法表示来描述简谐振动。
还有一种矢量图法,或称参考图法,能更直观地认识简谐振动的位移和时间的关系,深刻领会表明简谐振动的三个物理量A,ω和α的涵意。如图1-30所示。在图平面内画轴OX,由原点坐标O作一个矢量。我们对这矢量作三条规定:1.它的长度等于振动的振幅A(所以又称振幅矢量)。
2.在t=0时,它与x轴所成的角等于初位相α。3.这个矢量以数值等于圆频率ω的角速度,在图平面内绕O点作逆时针方向的匀速转动。这样一来,振幅矢量在旋转时,它在x轴上的投影OP,就代表了给定的简谐振动x=Acos(ωt+α)。道理是:在时刻t,振幅矢量和x轴所成的角为(ωt+α),由直角三角形OPQ可以得到,振幅矢量在x轴上的投影为Acos(ωt+α),正好代表了简谐振动的位移x。
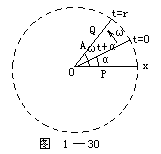
归纳起来,表示一种振动共有四种方法:
![]()
(2)三角函数法:x=Acos(ωt+α)。
(3)振动图线法。
(4)矢量图示法。
上述四种方法,在中学物理教学中都用到了,在机械振动部分就利用第(1)、(2)种方法;在交流电部分就用到第(3)、(4)种方法。各种方法是分别从不同的角度来反映简谐振动。因此必须掌握它们的特点。简谐振动是最简单、最基本的振动,一切复杂的振动都可以看作是若干个振幅、频率不同的简谐振动的合成。
【等幅振动】振幅保持不变的振动称作“等幅振动”。物质系统作受迫振动达到稳定状态,即外力对系统所作的功恰好补偿系统因阻尼而耗散的能量时,系统的机械能保持不变,系统的振动也就稳定下来,振幅保持不变,而成为等幅振动。
【固有振动】又称自由振动、本征振动。物理系统(包括机械、电磁或其他类型的振动)从外界取得一定的能量,开始振动以后,不再受外界作用而阻尼又可忽略的情况下,仅在内部弹性力或准弹性力作用下以固有频率而保持振幅恒定的振动状态叫“固有振动”。固有振动的振幅决定于系统开始振动时所具有的能量,但频率则完全取决于系统本身的性质(如弹性和惯性,电容和电感等)。被击动后鼓膜的振动,弹簧振子偏离平衡位置后无外力作用下的振动等都是“自由振动”。
【自由振动】见“固有振动”条。
【固有周期】物体作固有振动时的周期称为“固有周期”。它是由振动系统本身的性质所决定的,而与振幅大小无关。例如,用不同倔强系数的弹簧分别连接质量相同的振子实验,可知弹簧的倔强系数越大,振动的周期越短;反之,用同一弹簧连接质量不同的振子做实验,结果表明振子的质量越大,周期就越大。由此可见,弹簧振子的振动周期是由倔强系数K和振子的质量m决定的,通过理论计算,可证明,弹簧振子的固有周期可由下式确定:
![]()
上式表明,弹簧振子的周期跟质量的平方根成正比,跟弹簧的倔强系数的平方根成反比,而跟振幅无关。
通过上述结论,可以理解:当振子的质量一定,弹簧的倔强系数越大,振子所受弹力就越大,加速度也越大,振子从最大位移处回到平衡位置所需之时间越短,则周期就越短;当弹簧的倔强系数一定,如振子的质量越大,加速度就越小,振子从最大位移处回到平衡位置所需时间越长,则周期也长;当振子的质量和弹簧的倔强系数都一定的情况下,若振幅大,振子在最大位移处起振时的加速度也大,速度增长得很快,虽然振子完成一次全振动通过的路径较长,但所用时间并不长,因此振动的周期与振幅的大小无关。
【固有频率】它是系统本身所具有的一种振动性质。当系统作固有振动时,它的振动频率就是“固有频率”。一个力学体系的固有频率由系统的质量分布,内部的弹性以及其他的力学性质决定。如弹簧振子的
![]()
![]()
(L)所决定,与振幅无关。
【单摆】又称数学摆。它是由一根上端固定且不会伸长的细线(细线的质量略而不计)和在下端悬挂的一个小球(可看作质点)所组成。线在竖直位置时,小球处于平衡位置O点,将小球从平衡位置略为移动后,小球在重力作用下,将返回到原来的平衡位置O,但在返回平衡位置O后,又因具有动能而继续向另一侧运动,小球就这样在竖直平面内作来回重复的运动,这种振动系统称为“单摆”。
在单摆定义中应注意几段话:1.“……不会伸长的细线……小球……”这是说摆球可以当作质点看待,细绳质量略而不计,摆长可看作是由悬点到小球球心间长度不变的距离。2.“……小球……”摆球由于体积小,在运动中空气阻力可略而不计,小球的振动可看作只是由重力和绳子弹力的合力引起的。3.“……略为移动……”单摆振动只有在振幅很小的时候才能看作是简谐振动,所以只能施以很小的外力使摆球略为移动,满足振幅很小的条件。一般说摆角≤5°。4.“……重复……”就是说,第二次全振动与第一次全振动所经过的过程是一样的,这是因为空气的阻力忽略不计。如果说“往复”,在阻厄振动的情况下,就不能算简谐振动了。5.“……在竖直平面内……”如果摆球运动不在竖直平面内,那么它就不是简谐振动了。因此对单摆必须严格定义。
单摆的周期T与摆长l以及摆所在地的重力加速度g值的大小有关,也与摆角(摆线和垂线所成的最大夹角θ)有关,而与重锤的质量m无关。数学表达式为(在摆角θ≤5°时,周期可用下式)
![]()
【相】也叫相位,位相或周相。相是一个无量纲的物理量,它的单位是弧度。“相”是一个用来反映振动物体运动状态的物理量。在简谐振动x=Acos(ωt+α)中,(ωt+α)叫振动的“相”。常数α叫振动的初相,即t=0时的相。(ωt+α)是决定质点在时刻t的运动状态(如位移)的重要物理量。振动的物理量在每一时刻的数值是不同的,这种不同就反映在相的不同上。
相这个名词在物理学中有多种不同的含义。例如,物态叫相;具有相同的成分及相同的物理、化学性质的均匀物质部分叫相;在电路中,每一个单独的电动势所构成的电路叫作一相;在力学中,相和相差的概念在振动和波的研究中具有重要的意义。
【相差】亦称“相位差”,“位相差”或“周相差”。两个振动量(随时间作周期性变化的量)的相位之间的差值即“相差”。在实际问题中,常常用相这个物理量来比较两个简谐振动的步调是否一致。两个振动的角频率相同时,步调是否一致,是由二者的初相所决定。如它们的初相相同,总是同时经过平衡位置,同时到达正的(或负的)最大位移,同时向同一方向运动,振动的步调就一致。如果它们的初相不相同,则振动的步调就不一致。即相差等于零或2π的整数倍时,称同相;相差等于π的奇数时,称反向。当一个振动量的初相大于另一个振动量的初相时,就称前者超前于后者,或后者滞于前者。
【角频率】振动(或振荡)频率f的2π倍。也称圆频率。一般用ω表示,ω=2πf。
【复摆】又称物理摆。当一个能绕定轴摆动的重物(轴线不通过重心)振动时,若振幅很小(重心到定轴的垂直连线与垂线形成的摆角不超过5°)也可看成是简谐振动。如用J表示物体对转轴的转动惯量,m为物体的质量,l为物体的重心与转轴的垂直距离,则复摆的振动周期数学表达式为
![]()
利用复摆可以计时或用以测定重力加速度。
【振动的超前与落后】在同一时刻,将两个相同频率的简谐振动的位相相比较
x1=A1cos(ωt+α1)
x2=A2cos(ωt+α2)
若α1>α2,则称振动α1的相位超前于振动α2的相位,简称α1超前α2,或称α2落后于α1,若α2>α1,则α2超前α1。|α1-α2|=δ称为两振动的相位差。参阅“相差”。
【受迫振动】系统在外部策动力作用下发生的振动叫“受迫振动”。受迫振动是物体在策动力的强迫下所产生的振动,它和自由振动不同。例如,扬声器中纸盒的振动、蒸汽机活塞的振动以及缝纫机上缝针的振动,都是受迫振动的例子。受迫振动开始的情况非常复杂,但经过一段时间后可以达到一种稳定状态。在稳定状态下,振动的频率即为策动力的频率,跟它固有的频率无关。振动的振幅保持恒定不变,振幅的大小不仅与策动力的大小有关,而且还跟策动力的频率以及系统本身的固有频率有关。实际上在这种受迫振动中,一方面系统因策动力做功而获得能量,另一方面又因有阻尼而使机械能损耗。开始时,策动力对系统作的功往往大于系统克服阻尼损耗的能量,总的趋势是振幅逐渐增大。由于阻力一般是随速度而增加的,所以当振动加强时,因阻力而损耗的能量也要增多。当策动力对系统作功而传递给系统的能量,恰好补偿系统因阻力而损耗的能量时,系统的机械能保持不变,振幅保持稳定,成为无阻尼等幅振动。受迫振动的基本特点就是:物体做受迫振动的频率等于策动力的频率,而跟物体的固有频率无关。
【阻尼振动】由于振动系统受到阻力作用造成能量损失而使振幅减小的振动叫“阻尼振动”。又称减幅振动。振动系统由于受到阻力(这种作用为阻尼),消耗系统能量做功,而使振动的能量不断地减少,由
![]()
间减少的同时,振动物体的振幅也逐渐减小,这是一种非简谐振动。这里所谓受到阻力、系统的能量减少,一般指两种情况:一种是由于摩擦阻力存在,使振动系统的机械能量逐渐转变为热运动的能量;另一种是由于振动系统引起邻近质点的振动而做功,并使它们振动起来,使系统的能量逐渐向四周辐射出去,转变为波动的能量。例如,簧片振动时,不仅由于摩擦而消耗能量,同时也因辐射声波而减少能量;电磁振荡回路中因电阻和电磁辐射而使振幅逐渐减小的振动;天平臂的摆动;电流计线圈的摆动都属于阻尼振动。在使用天平和电流计时,总希望它们能很快地达到平衡位置,为使振动的衰减加快,而增大对振动的阻尼。增大阻尼常用机械或电磁的方法,如天平中的空气盒,电流计中的阻尼线圈等。
【阻尼因数】阻尼振动中描述阻尼程度的一个物理量。或称“减缩量”。阻尼振动的振幅随时间衰减规律的公式是A=A0e-βt,式中t为时间,e为自然对数的底,A0为初始时刻的振幅,β称为阻尼因数。阻尼因数β愈小,振幅衰减愈慢;反之,β愈大,则振幅衰减就愈快。若相邻两振幅为A1、A2,对应的时间为t与(t+T),则阻尼因数=
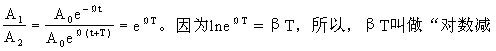
缩[量]”,β又叫“衰减常数”,T是振动的周期。
【临界阻尼】任何一个振动系统,当阻尼增加到一定程度时,物体的运动是非周期性的,物体振动连一次都不能完成,只是慢慢地回到平衡位置就停止了。当阻力使振动物体刚能不作周期性振动而又能最快地回到平衡位置的情况,称为“临界阻尼”,或中肯阻尼状态。如果阻尼再增大,系统则需要很长时间才能达到平衡位置,这样的运动叫过阻尼状态,系统如果所受的阻尼力较小,则要振动很多次,而振幅则在逐渐减小,最后才能达到平衡位置,这叫做“欠阻尼”状态。
【无阻尼振动】机械振动按振幅的变化来区分,可分为无阻尼振动和阻尼振动。物体作无阻尼振动,并不一定指它不受阻力,而是指它在振动过程中保持振幅不变。无阻尼振动又可分为两种:一种是无阻尼自由振动,即振动物体只受回复力作用,不受任何阻力作用,不对外做功,系统无能量损失,这就是一种理想情况,是“简谐振动”。另一种实际上是“受迫等幅振动”,即振动时系统从外界取得的能量,刚好补偿在振动过程中所损耗的能量,系统的能量、振动物体的振幅都保持不变。
【共振】一个振动系统,当外加的策动力的频率与系统本身的固有频率很接近或相同时,系统受迫振动的振幅将趋于最大值,这种现象叫
![]()
![]() 上式中的A0为受力F0作用而达平衡时的最大位移,即静振幅,所以共振
上式中的A0为受力F0作用而达平衡时的最大位移,即静振幅,所以共振
![]()
![]()
种特殊情况。从力的角度看,要求周期性变化的策动力的方向跟振动物体的运动方向相同,凡是跟振动物体运动方向相反的力都会促使振动物体的振幅减小。策动力频率变化跟系统的固有频率越接近,使物体振幅增加的力作用次数就越多。当策动力的频率与系统的固有频率相等时,并且策动力的位相跟物体运动的位相同相时,策动力的每一次作用都将使物体的振幅增加而达到最大值。若从功能关系来说,就要求在任何时刻,周期性变化的策动力对振动系统做正功。在一个振动周期中,由于策动力的频率和系统的固有频率不同,因此策动力的方向和物体运动的方向有时一致,有时相反。当方向一致时,供给系统振动能量,对物体做正功;当方向相反时,使系统振动能量减少,而对物体做负功。只有在策动力频率跟振动系统的固有频率相同,且位相相同时,才有可能使其方向在整个周期中跟物体运动方向一致,从而达到在任何时刻做正功的效果。系统能量不断增加,振幅不断增大,直到策动力做功供给系统的能量等于克服摩擦阻力消耗的能量,振幅不再增大,即达到了最大的振幅。因为在物体作无阻尼自由振动时,外力的频率等于振动体的固有频率就会发生共振,由于实际的振动多少存在一些阻尼作用,策动力在频率要稍稍偏移振动体的固有频率才能发生共振,在这种情况下,只能说“接近固有频率”,而不说“等于固有频率”。
在许多情况下要利用共振现象,例如,收音机的调谐就是利用共振来接收某一频率的电台广播,又如弦乐器的琴身和琴筒,就是用来增强声音的共鸣器。但在不少情况下要防止共振的发生,例如,机器在运转中可能共振而降低精密度。上世纪中叶,法国昂热市附近一座长102米的桥,因一队士兵在桥上齐步走的步伐周期与桥的固有周期相近,引起桥梁共振,振幅超过桥身的安全限度,而造成桥塌人亡事故(死亡226人)。
【策动力】一般指外力而言。这里策动力可以是简谐力(即其大小随时间按正弦或余弦规律变化的力),如电动机转动时对机座产生的作用;也可以是非简谐力,如人们对秋千的推力。
【振动迭加原理】当一个振动系统受两个或两个以上简谐强迫力作用时,振动系统的稳态响应就是在各简谐强迫力作用下系统的稳态响应的合成,称为“振动迭加原理”。不同频率的谐振动迭加(合成)后,不再是谐振动,称为非谐振动或振动。根据这一原理可解决两个或多个简谐振动合成的问题,它不仅在振动中重要,在波的传播过程中也很重要。
【拍】它是一种重要的振动合成的现象。两个振动方向相同的简谐振动,若它们的频率之和远大于它们的频率之差时,合振动的振幅发生周期性的、明显的变化,这种现象称为“拍”。设有两个频率相近,振幅相等,初位相相同和振动方向相同的谐振动,如下式
x1=A0cos(ω1t+φ)
x2=A0cos(ω2t+φ)
它们叠加的结果是
![]()
合振动不是简谐的,因为合振幅
![]()
是周期性变化的,振幅或能量的周期性变化称为拍。因振幅(正值)的周期为π,故拍的频率
![]()
为两振动之差。若两个频率相差不多,拍的频率便较小。当两个频率相差很小的音叉同时振动时,声音强度有节奏的时强时弱现象就是声拍,利用这个现象可以校准乐器的频率或进行声频的测量。在声学中,拍曾称为拍音、升沉和念。
【拍频】同向进行之波列频率接近时,其干涉作用形成定时强弱的规律。它每秒间的拍数称为“拍频”,即为二波频率之差。若使一发声体每秒之振动数为m,另一发声体每秒之振动数为n,而m较n大,此
![]()
![]()
动一次,故得
![]()
∴x=m-n
例如两个音叉的频率,一为251,一为250,当同时敲两音叉时所合成之声波,其拍频为1。
【波】也称波动。从平衡位置发生的任何扰动,在介质中传播的过程叫做“波”或“波动”。波动是能量传递的一种形式。
波有多种形式,最常见的是机械波(如水波、声波等)和电磁波(如光波)。机械波以实物(固体、液体或气体等)为传波媒质,电磁波是场传播的一种形式。在力学中所提到的波都是机械波。因此波是一种机械运动的形式。形成波必须有两个条件:振源及弹性媒质。只有在弹性媒质中,某个质点的振动才能带动与其相邻的质点运动。波动过程中的媒质质点只在平衡位置附近振动,而并不沿着振动传播的方向迁移。波传递的是能量,原来不动的质点,在波动所及时,发生了振动,获得了能量。实际上可以认为,传播的弹性媒质的各个质点间是以弹性力互相联系着的。这样,如果媒质中有一个质点A,因受外界扰动而离开平衡位置时,A点周围的质点,对A将产生弹性力,使A回到平衡位置,并在平衡位置附近作振动。与此同时,A点周围的质点也受到A的弹性力,它们也离开各自的平衡位置振动起来。所以,媒质中一个质点的振动会引起邻近质点的振动,而邻近质点的振动又引起较远质点的振动。从上述情况来看,波在媒质中所表现的运动状态,其特点是相邻质点的振动位相依次落后,而且是振动位相的传播过程,而所有质点都仍在各自的平衡位置附近振动。
【波源】即振源。凡能引起波动的作机械振动的物体称“波源”。
【横波】质点的振动方向与波的传播方向垂直,这样的波称为“横波”。横波在传播过程中,凡是波传到的地方,每个质点都在自己的平衡位置附近振动。由于波以有限的速度向前传播,所以后开始振动的质点比先开始振动的质点在步调上要落后一段时间,即存在一个位相差。横波的传播,在外表上形成一种“波浪起伏”,即形成波峰和波谷,传播的只是振动状态,媒质的质点并不随波前进。实质上,横波的传播是由于媒质内部发生剪切变形(即是媒质各层之间发生平行于这些层的相对移动)并产生使体元恢复原状的剪切弹性力而实现的。否则一个体元的振动,不会牵动附近体元也动起来,离开平衡位置的体元,也不会在弹性力的作用下回到平衡位置。固体有切变弹性,所以在固体中能传播横波,液体和气体没有切变弹性,因此只能传播纵波,而不能传播横波。液体表面形成的水波是由于重力和表面张力作用而形成的,表面每个质点振动的方向又不和波的传播方向保持垂直,严格说,在水表面的水波并不属于横波的范畴,因为水波与地震波都是既有横波又有纵波的复杂类型的机械波。为简便起见,有的书中仍将水波列为横波。
【纵波】亦称“疏密波”。振动方向与波的传播方向一致的波称为纵波。纵波的传播过程是沿着波前进的方向出现疏、密不同的部分。实质上,纵波的传播是由于媒质中各体元发生压缩和拉伸的变形,并产生使体元恢复原状的纵向弹性力而实现的。因此纵波只能在拉伸压缩的弹性的媒质中传播,一般的固体、液体、气体都具有拉伸和压缩弹性,所以它们都能传递纵波。声波在空气中传播时,由于空气微粒的振动方向与波的传播方向一致所以是纵波。
【水面波】它既不是纵波,也不是横波。它是因重力以及表面张力的作用,在水表面上传播的波。在其波动过程,水的质点运动较为复杂。如果水表面上某一质点由于外力作用而下降,形成水窝。在重力和表面张力的作用下,周围的质点开始向下降处流动,填充水窝的凹部,并在其四周形成圆形凹槽。在这凹槽外沿上的水的质点,继续向低处汇流,使圆槽直径增大。在圆槽里面的水的质点,将向上“浮出”而形成凸峰。当这部分质点再次下降时,凸峰将以圆圈状向外传播开去,形成了水面波。在下降时水的质点除了向下运动外,还向波源方向运动;而在上升时它们除向上运动外,还向波源的反方向运动(即背向波源方向)。随着水的质点在其平衡位置附近做周期性的运动,水面波逐渐向外传播。
【弹性波】弹性介质中物质粒子间有弹性相互作用,当某处物质粒子离开平衡位置,即发生应变时,该粒子在弹性力的作用下发生振动,同时又引起周围粒子的应变和振动,这样形成的振动在弹性介质中的传播过程称为“弹性波”。在液体和气体内部只能由压缩和膨胀而引起应力,所以液体和气体只能传递纵波。而固体内部能产生切应力,所以固体既能传播横波也能传播纵波。
【波长】沿着波的传播方向,两个相邻的同相位质点间的距离叫做“波长”。它是指波动媒质中,任意两个相位差为2π的质点之间的距离。例如,纵波中,两个相邻疏部中央间的距离或两个相邻密部中央间的距离也都等于波长。在横波中,两个波谷间的距离或两个波峰间的距离也都等于波长。由波速、波长的定义可知:在质点振动的一个周期内,振动状态传播的距离恰是一个波长,所以λ=v/f,或λ=vT。由上式可以看出,同一频率的波,在不同媒质中的波速是不同的,因而波长也就不同。式中λ表示波长。波长、波速和波源振动频率,称为波的三要素。
【波速】波传播的速度。波速只决定于介质本身的惯性和弹性而与波源的振动频率无关。例如,在固体介质中,横渡和纵波的传播速度分别为
![]()
式中G和r分别为介质的剪切弹性模量和杨氏弹性模量,ρ为介质的密度。在气体和液体介质中纵波的传播速度
![]()
式中K为介质的体积弹性模量,ρ为介质的密度。对于单色波来说,波速等于相速度,其数值等于波长λ和波源振动频率f的乘积,即
v=λf
波动存在三种速度,在物理意义上却有明显的区别。
1.质点速度:介质的质点在其平衡位置附近作简谐振动的速度。
2.波速或相速度:等相位面(如波峰或波谷)在介质中传播的速度。在中学物理课中讲的波速就是相速度。
3.群速度:即波群传播能量的速度。由一系列波长和频率不同的分波叠加而成的合成波。若各个分波在介质中传播时的相速度各不相同,则群波的波形将随时间变化,其振幅最大部分的运动速度称为群波的群
![]()
![]()
![]()
【波峰】在横波中,某一时刻波到达的各点都处于不同的振动状态,当处于波形最突起的地方,即此时那一点的纵向位移具有正向最大值的位置称为“波峰”。例如水波突起的最高处。
【波谷】在横波中,某一时刻波到达的各点都处于不同的振动状态,当处于波形最凹下的地方,即此时那一点的纵向位移具有反向最大值的位置称为“波谷”。例如水波凹下的最低处。
【行波】从波源向外传播的波称“行波”。又称“前进波”。除驻波外,一般的波都是行波。
【波形】波形是指位移对于质点坐标的曲线形状。是在波的传播过程中,由反映波线上一系列介质质点在某一时刻的位移值的点所连接而成的曲线图形。纵波的波形只是间接地反映疏部和密部相间的图形;横波的波形是波峰和波谷相间的图形。行波的波形是以波速沿着波的传播方向行进的;而驻波的波形永不前进,而是在原地变化,已知某时刻的波形为f(x),则任一时刻的波形必为Kf(x),其中K为与x无关的常数。
【波的迭加原理】反映波动属性的基本原理之一。它是从大量实验事实中总结出来的。由不同波源产生的几列波在同一介质中传播时,每列波都会保持各自的特性(频率、波长、振幅、振动方向和传播方向等),每一列波并不因其他波的存在而改变其传播规律。在几列波相遇的区域内,任一介质质点的振动等于各列波单独传播时在该位置所引起的振动之和,这叫做“波的迭加原理”。例如,乐队合奏或几个人同时谈话时,不因声波在空间互相交迭而改变原来声音的特色,我们仍能清楚地辨别出各种乐器或每个人的声音来。又如将两个小石块同时投入静水池中,它们将各以投入点为圆心,激起一列圆形波纹。这两列波在水面传播时相遇,交叉而过,每列波的波前并不因遇到另一列波面而改变形状,原来圆形波前仍保持其圆形波前,好像在传播的过程中并没有遇到其他波一样,每列波的特性,也不会因其他波的存在而改变。其他如光波、声波也同样具有这种独立传播的特性。
【波的衍射】亦称波的“绕射”,是波的重要特性之一。是指波在传播过程中,遇到障碍物或缝隙时传播方向发生变化的现象。水波、声波、光波都能发生衍射现象。障碍物或缝隙的宽度越小,而波长越大,则衍射现象就越明显。波绕过障碍物或通过小孔绕到障碍物的背后。这种波能绕过障碍物继续传播的现象,叫“波的衍射”。室内发出声波可以绕过门、窗而到达室外的各角落。如果障碍物或缝隙的宽度远远超过波长时,波的衍射现象就不明显。波的衍射现象可用惠更斯原理来解释。
【波的干涉】由两个或两个以上的波源发出的具有相同频率,相同振动方向和恒定的相位差的波在空间迭加时,在交迭区的不同地方振动加强或减弱的现象,称为“波的干涉”。符合上列条件的波源叫做“相干波源”,它们发出的波叫做“相干波”。这是波的迭加中最简单的情况。
二相干波迭加后,在迭加区内每一位置有确定的振幅。在有的位置上,振幅等于二波分别引起的振动的振幅之和,这些位置的合振动最强。称为“相长干涉”;而有些位置的振幅等于二波分别引起的振动的振幅之差,这些位置上的合振动最弱,称为“相消干涉”。它是波的一个重要特性。在日常生活中最常见的是水波的干涉,利用电磁波的干涉,可作定向发射天线,利用光的干涉,可精确地进行长度测量等。
【驻波】在同一媒质里,两个频率相同、振幅相等、振动方向相同、沿相反方向传播的行波迭加而成的波叫“驻波”。它是局限于某一区域而不向外传播的波动,获得驻波的方法是让前进波与反射波迭加而成。这是干涉的一种特例。两列波方程分别是
![]()
![]()
驻波的特点。各点均作简谐振动,但其振幅随x作周期性的变化,有些
![]()
![]()
![]() 的那些点始终不动,它们位于
的那些点始终不动,它们位于
![]()
![]()
间所有的点同时达到各自的最大位移;cosωt=0时,所有的点同时通过平衡位置,即相邻波节间的点振动相位相同,而波节两侧的点振动相位相反。当各点同时达到各自的最大位移时,速度均为零因而动能为零,势能即总能,此时主要集中在波节附近,因为此时波节处的形变最大。当各点同时通过平衡位置时,势能均为零,动能即总能,此时主要集中在波腹附近,因为波腹附近点的速度最大。由此可见,驻波并不是能量的传播过程,而是在波腹与波节间动能与势能的相互转换。驻波与行波不同,它无所谓传播的方向,亦不能传播任何能量,实质上它是介质的一种特殊的振动状态。
【波节】在驻波系统中振幅为零的点。详见“驻波”。
【波腹】在驻波系统中振幅最大的点,位于两相邻的波节之间。详见“驻波”。
【冲击波】又称激波。由非线性振动引起的,并以超音速传播的表示波的特性的物理量,几乎是不连续的声波。例如爆炸,在它的波前后面将出现介质质点的密度、速度和温度的急剧变化,因而产生高压和高温。
【波面】也称波阵面。从波源发出的振动,在传播过程中,在媒质中振动相位相同的点组成的面称为“波面”。例如;以石投入静水中,水波的波面是许多同心圆。最前面的一个波面称为波前。波前上点的位相与波源的初位相相同。与波面垂直、且指向波的传播方向的线称为波线。波面、波前、波线是对波的运动状态的描述,对波的理解很重要。
【波前】详见“波面”。
【波线】详见“波面”。
【平面波】■面是平面的波。平面波的波线是一束与波面垂直的平行线,它是一个理■如波源是由振动状态相同的点组成的平面,在距波源不太远处可■波源足够远处的球面波亦可看作是平面波。例如射到■就可以认为是平面波。
【球面波】■的波。其波线是自球心引出的一簇射线。球心是点波源■存在的,因而球面波是一种理想模型。例如,从点光源发出的光波,在均匀的各向同性媒质中传播时,就是一种球面波。
【表面波】通常在液体或气体之间的表面上传播的机械波。由于各物质粒子振动的振幅随粒子在表面下的深度的增加而迅速减小,因此这种波只存在于表面附近,由于表面张力而引起振幅很小的表面波,叫张力波。如水面上的微小波纹,在液面由于重力作用而产生的表面波称重力波。如水波等。
【波的反射】波由一种媒质达到与另一种媒质的分界面时,返回原媒质的现象。例如声波遇障碍物时的反射,它遵从反射定律。在同类媒质中由于媒质不均匀亦会使波返回到原来密度的介质中,即产生反射。
【波的折射】波在传播过程中,由一种媒质进入另一种媒质时,传播方向发生偏折的现象,称波的折射。在同类媒质中,由于媒质本身不均匀,亦会使波的传播方向改变。此种现象也叫波的折射。它也遵从波的折射定律。
【波的图象】在平面直角坐标系中,用横坐标表示在波的传播方向上各个质点的平衡位置与参考原点的距离,用纵坐标表示某一时刻各个质点偏离平衡位置的位移,连接各位移矢量的末端所得到的曲线,就叫“波的图象”也称为波形。利用波的图象,可以形象地反映出通过机械波的媒质区域中,某一时刻每个质点偏离平衡位置的位移对空间的分布规律。由简谐振动在媒质中传播所形成的波——简谐波,在任何时刻的图象都是余弦(或正弦)曲线,而媒质质点的振动图象也是余弦(或正弦)曲线。这两条曲线变化规律相同,但它们的物理意义不同。振动图象的横坐标表示时间,纵坐标表示某一质点在各个时刻的位移;波的图象的横坐标是质点的位置,而纵坐标表示的是某一时刻各个质点的位移。在振动图象中,相邻两个最大值之间的间隔等于周期T。在波的图象中,相邻两个最大值之间的距离等于波长λ。振动曲线是跟踪一个质点标记出它的位移随时间变化的情况,就好像是给该质点拍的“电影”。而波形曲线则是记录了某时刻波线上各点相对平衡位置的位移情况,就好像给波线上全体质点照的一张“像片”。见图1-31和图1-32所示。
【声学】物理学的一个分支,是研究声波的产生、传播、接收和作用等问题的学科。根据研究的方法、对象和频率范围的不同,它与许多其他学科交叉在一起,形成了很多独特的边缘学科,例如,大气声学、水声学、电声学、生物声学、心理声学、语言声学、建筑声学、环境声学、几何声学、物理声学、生理声学、分子声学、声能学、超声学、次声学、微观声学、音乐声学、振动与波动声学、噪声控制学等部分。随着近代工业发展起来的声学,是古典声学、电子技术和各种工业应用相结合的产物,它还在随着工业的发展而继续发展。
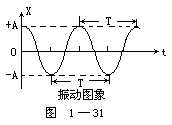
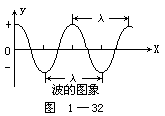
【音】即“律音”。具有单一基频的声音。纯律音(或纯音)具有近似于单一的谐振波形。这种律音可由音叉产生。乐器则产生复杂的律音,它可以分解成一个基频以及一些较高频率的泛音。参见“音品”。
【声源】一个向周围媒质辐射声波的振动系统叫“声源”。例如,二胡、小提琴等弦乐器是靠弦的振动发声;笛子等管乐器是靠空气柱的振动发声;锣、鼓等膜乐器是靠板或膜的振动发声;唱歌或说话是靠咽喉声带的振动发声。任何发声的物体都在振动着,所以把各种振动着的发产物体,叫做声源。固体、液体、气体都能振动发声,都可视为声源。
【声波】弹性媒质中,各质点振动的传播过程称为“声波”。它是一种机械波。起源于发声体的振动频率在20赫兹与20000赫兹之间的声波能引起人的听觉,故又称可听声波,频率在10-4~20赫兹的机械波称为次声波,频率在2×104~2×108赫兹的机械波称为超声波。次声波和超声波一般不能引起人的听觉。从物理的观点来看,频率在20~20000赫兹的声振动与这个频率外的声振动没有本质上的不同。因此,广义的声波包含次声波与超声波在内。是否能引起人的听觉,不完全由机械波的频率决定,还与声强有关。声波在固体中以纵波和横波两种形式传播,但在液体和气体中,则只能以纵波的形式传播。
【声速】又称音速。是指声音在介质中的传播速度。它与介质的密度、弹性系数以及介质所处的状态有关。在固体中声波可以纵波和横波两种形式传播,其纵波的传播速度
![]()
E是固体的弹性模量,ρ是它的密度。
在气体和液体中声波是纵波,其传播速度
![]()
K是介质的体积弹性模量。
声音在空气中的传播速度随温度的升高而增大,它与绝对温度T的
![]()
其中r为定压比热Cp与定容比热Cv之比,R为气体恒量。通常以下式表示
vt=331.45+0.6lt
vt是t℃时空气中的声速,单位是米/秒,331.45米/秒是0℃时空气中的声速。温度每升高1℃,声速约增加0.6米/秒。
【声波的反射】声源发出的声波,在传播过程中遇到障碍物时声波反射回来,谓之“声波的反射”。北京天坛公园的回音壁、山谷中的回声、雷鸣,以及建筑物内的交混回响都是声波反射现象所造成的不同情况。
【回声】当声投射到距离声源有一段距离的大面积上时,声能的一部分被吸收,而另一部分声能要反射回来,如果听者听到由声源直接发
![]()
音,这种反射回来的声叫“回声”。如果声速已知,当测得声音从发出到反射回来的时间间隔,就能计算出反射面到声源之间的距离。利用这个道理,已设计成水声测位仪,用以测量海水的深度。回声是山谷中或大厅中常有的现象,夏天响雷轰轰不绝,也是雷声经天空密云层多次反射的回声。广义讲,凡有这种性质的其他信号,都属回声。例如,反射回来的超声波信号。利用回声制造的回声探测仪、水声定向器、超声波探伤仪等,用声波探测鱼群、或用地面上爆炸声波的反射用以探测地下的油矿等。
【交混回响】声源停止作用后,声音的延续现象称为“交混回响”。在各种建筑物中,声波要经过墙壁,天花板等多次反射和吸收。混响持续时间的长短和反射声波的材料对声波的吸收有关。如果每次只吸收很少一部分声能,则混响时间延长,使声音前后重迭辨别不清感到声音模糊。如果混响时间过短,虽然对声音分辨很清楚,但使人对声音听起来枯涩、单调,有沉寂枯燥的感觉,对音乐演奏的效果很不适宜,影响对演奏的欣赏。一般适当的时间在1~2秒之间,使混响时间降低60分贝。各种物质的吸声性质用吸声系数来表示,吸声系数即吸收的声能在入射波能量中所占的百分比。软而多孔的物质吸声系数大,而坚硬平滑的物质吸声的系数就小。所以,交混回响时间的长短,是建筑物重要的声学性质。例如,北京首都剧场的交混回响时间,满座时是1.36秒,空座时是3.3秒。北京人民大会堂的交混回响时间,满座时是1.6秒,空座时是3秒。
【声波的干涉】可用音叉演示声波的干涉。音叉的两个叉股是两个相同的波源,当音叉发声时,辐射出的两列波发生干涉,使音叉绕叉柄的纵轴旋转,或音叉不动,我们环绕正在发声的音叉走一周,会听到音叉的声音忽强忽弱。当音叉产生的两列波发生干涉时,会出现相间的加强区和减弱区。在加强区,空气的振动加强,我们听到的声音也强。在减弱区,空气的振动减弱,我们听到的声音也弱。声波的干涉是指在同一区域中,两列频率相同的持续声波相遇而迭加的现象,它只能在特定的条件下发生,不是常见的现象。
【声波的衍射】声波在通常情况下,有的表现为直线传播,有的会发生明显的衍射。由于声波的波长约在1.7厘米到17米之间,它跟一般室内的障碍物以及门窗等物的尺寸相接近,当声波在传播过程中,碰到与声波波长差不多的障碍物,声波就能绕过障碍物传到它的背后去,即发生衍射现象。
【共鸣】发声器件的频率如果与外来声音的频率相同时,则它将由于共振的作用而发声,这种声学中的共振现象称作“共鸣”。许多乐器应用振动体和空气柱的共鸣,来增强乐器发出的声音。使两个共鸣箱相对放置(箱口相对),然后敲击一共鸣箱上的音叉,过一段时间后,以手握住被敲击的音叉,使其停止振动,此时可听到另一个未被敲击的共鸣箱发出声音,从而证实共鸣的产生。由于二共鸣箱之一发生振动,附近空气向周围传播,另一共鸣箱和音叉即发生共鸣,故也能发出声音。当两个物体的固有频率相同,或其中一个是另一个作为声源的固有频率的整数倍时,就会发生共鸣。音叉下面所附的音匣是起着使声音加强的作用。弦乐器如小提琴、琵琶、二胡等的琴身或琴筒,也都具有音匣的作用。从前,所建戏台,往往在舞台下面放置几口大缸,同样是利用共鸣作用使台上演员和乐器发出的声音造成宏亮而圆润的效果。
【空气柱的共鸣】向细玻璃管的一端吹气,或将振动着的音叉放在管口处,可以听到管内空气发出声音。这就是说,管内空气柱由于自身的振动而成为一个发声体。若将一玻璃管的下端与盛有水的漏斗用皮管连通。把一个频率为v的振动着的音叉放近管口,上下移动漏斗,用以改变管中空气柱的长度。在某一长度处能听到声音最大,这是因为管中的空气柱在音叉产生的连续正弦声压的振动作用下,发生了受迫振动,当音叉振动频率恰好与空气柱的固有振动频率重合时,发生了共振。慢慢调节,使管内水平面继续下降,还可在其他几个适当的空气柱长度,听到声音的强度达到最大值。管内空气柱的这种由声波的作用而引起的共振现象叫做声的共鸣。空气柱的长度L与声波的波长λ有如下的关系:
![]()
又因为声源音叉的频率v固定不变,而空气柱中的声速v又有确定值,所以由发生共振的特定波长λ=u/v可得其共鸣频率。利用气柱共鸣可以方便地测定声波的波长,从而可推算出声速。
【音叉】一种声学仪器,用钢制成形如字母U,但是做得细而长,下端的柄插在一端开口的空木箱上,用以增加发音强度。音叉的振动频率一定,则其音调高低一定,且其振动为棒的振动,所发之声极清朗。故常用它作为测定音调的标准。用橡皮锤轻敲音叉之上端,则其两叉股左右振动而发声。又音叉音之高低,视其叉股之长短厚薄而定。股臂长而薄者振动缓而音低;股臂短而厚者振动急而音高。
音叉的振动通常不易产生泛振动,偶尔产生泛振动,亦因棒之阻抗大而即时消减,因此音叉容易产生基振动。音叉振动时,亦有干涉的现象产生,其两叉股的振动,系同时向内或向外。若两叉股同时向内振动,其间a成稠密状,如图1-33所示,而叉股外侧b和b′即成稀疏状,等到两叉股同时相背向外振动时,则中间变成稀疏,而b和b′处变成稠密。因为音叉的两叉股振动的振幅和波长或频率均相等,故如图1-33中虚线所示位置,疏密相遇,产生干涉,则无声。这可将振动音叉,放在耳边,徐徐转动,而找到这样无声区域的位置。
音叉能在很长时间内保持其音的频率不变,振动的振幅和温度都不容易使频率改变。音叉的频率有高达每秒9万周者。通常音叉都用钢或弹性钢制成。因音叉尺寸不大,发声的输出很少传入空气中,又因其振动方法,只有极少量的纵波成分沿叉柄振动,故此振动系统的阻滞极少。用音叉木柄与共鸣器相连,可增加声音输出,且因共鸣器与音叉的泛音并不相同,故只有基音产生共鸣。音叉的用途很多,在调乐器时,音叉被用作音调标准。
【音调】声音的高低叫做“音调”。音调的高低,主要取决于声波频率的高低。当声波的强度增加,亦会使同一频率的声波有音调较高之感。通常乐器所发出的声波均非单音或纯音,而有其波形的复杂性,故音调的高低,实际是由很多因素所决定。乐音与噪音的区别,在于乐音有一定的频率,而噪音的频率是经常在变化的,它使人们有快速音调变化之感。在音调上有基音与泛音之别,泛音即其振动频率为基音的整数倍,有第一泛音,第二泛音等等。在波动中,周期与频率成反比,所以泛音周期比主周期短,它们的比例也是整数倍。
男子发音,其频率约在90~140Hz之间,其音较低。妇女发音的频率约在270~550Hz之间,其音较高。人耳器官所能感受音波频率的范围因人而异,一般人的听觉范围由50~15000Hz,听觉灵敏的可由20~20000Hz。人类口腔发声大约是100~8000Hz。各种乐器的频率范围是40~14000Hz,扬声器的频率是40~8000Hz。如声音由张紧的弦发出,则弦越细、越短、张的越紧,音调便越高;反之音调就低。
【响度】又称音量。人耳感受到的声音强弱,它是人对声音大小的一个主观感觉量。响度的大小决定于声音接收处的波幅,就同一声源来说,波幅传播的愈远,响度愈小;当传播距离一定时,声源振幅愈大,响度愈大。响度的大小与声强密切相关,但响度随声强的变化不是简单的线性关系,而是接近于对数关系。当声音的频率、声波的波形改变时,人对响度大小的感觉也将发生变化。
【音品】声音的品质叫音品,也称“音色”,是声音的属性之一。它由泛音的多少、泛音的频率和振幅所决定。不同的乐器在基本振动频率相同的情况下,仍然可以区分其各自的特色,就是因为它的音色不同。例如合奏的二胡、月琴、琵琶,由于音色不同,人们的听觉可以分辨各乐器名称。
【声音的三要素】音色、音调、响度是声音的三个主要属性,故称它们是声音的三要素。
【基音】在复音中,频率最低的声音叫做“基音”。乐音的音调是由基音的频率决定的。例如100Hz的钢琴声,除发出频率是100Hz的声音外,还同时发出许多较弱的不同频率的声音,100Hz的纯音叫钢琴的基音。
【泛音】频率为基音的整数倍或大于1的非整数倍的其余纯音称作“泛音”。等于基音频率整数倍之声音又称为谐音。作简谐振动的发声体,发出的是非常单纯的纯音。乐器发出的声音,一般是由若干个频率和振幅都不同的纯音所组成的复音,其中频率最低的纯音称基音,还有频率是基音整数倍的泛音。乐音的音品就是由泛音的多少及其频率和振幅决定的。
【声压】由于声波作用而产生的压强叫“声压”。声波在传播过程中,空气中任一点附近质点由于声波作用,时而疏松,时而紧密,因而压强也相应地忽强、忽弱变化。当空气中有声波传播时该点的压强与没有声音到达时的压强之差叫做该点的声压。声压的单位是帕斯卡,简称帕。声压的大小和传声介质中质点在声波作用下振动速度、介质的密度以及声波的传播速度有关。如用ρ表示空气密度,μ表示声速,v是空气质点的振动速度,则声压P为
P=pμv
树叶被微风吹动的响声声压约为0.01帕;在房中大声说话的声压约为0.1帕。
【声强】声波传播的能流密度。即在单位时间内通过垂直于传播方向上单位面积的声音能量。由于声音的强弱与声源的振幅有关。若声源的振幅大,单位时间内传出去的能量就大,因而声波也就较强。声源在某点发出的声波,向外传播,在距波源r处的声强为
![]()
式中E是声源每秒钟发出的能量,声强I的单位是瓦/米2。声强与声音传播的距离有关,跟响度有关,但响度随声强的增加并不呈线性关系,两者是有区别的。声强是客观存在事实,它是声音强弱的物理量,不受人耳功能的影响。但响度却与人的感觉有关,当声波引起耳膜振动时又因人而异,对同一声强的声波反映不同,耳感灵敏者觉得响度大,而耳感差的就觉得响度小。对不同频率的声波,耳感亦不相同。凡能引起正常听觉的声波,对声强有一定范围的要求,对于每个给定的频率,要引起听觉,其声强也有两个极值。若根据正常听觉的实验结果,以频率为横坐标,以声强为纵坐标,将各种频率的声强上下限坐标连起来,低于下限的声强,不能引起听觉。凡超过上限的声强,使人耳有痛感。故上限曲线叫痛觉阈,下限曲线叫可闻阈,两曲线间的区域即为听觉范围。因此凡能引起人的听觉的声波,除对频率要求在20~20000赫兹外,还要求声强范围在10-12瓦/米2~1瓦/米2。由此可见声强变化范围是很大的。
【声强级】声强的量度。声强I与标准声强I0之比的对数称作声强I的“声强级”,用L表示,即
![]()
单位为贝尔,用Bel表示,这个单位在实用上太大,故常用贝尔的1/10,即分贝(用dB表示)作为单位,所以声强级的表示式为
![]()
I0为声强的参考标准,国际上选定I0=10-12W/m2,即可闻阈的声强值。
![]()
最轻声就是0。通常在谈话时的声强级为60~70dB。
【乐器】演奏音乐、戏曲伴奏、电影中的音响效果等所用的器具。一般是按发音来分类,如管乐器:它的发声是靠空气柱的振动而取得效果,这类器具有,笙、管、笛、箫等;弦乐器,是靠弦的振动而发声,如,月琴、琵琶、提琴、二胡、马头琴等多种;打击乐器,是利用打击发声的,如鼓、锣、铃、钹、钗等。
【乐音】凡由声源按周期性振动而有规则的声音,令人悦耳动听谓之乐音。它的波形图线是周期性的曲线。乐器按规律振动的才是乐音,否则即是噪音,刺耳难听。乐音的三要素是音调、响度和音品,它们各自反映乐音的特性。
【噪音】它是由声源作无规则的,非周期性振动所产生,或是由不同强度和不同频率的声音无规律的组合在一起而形成的。例如,车辆的发动机、喇叭声,工地或工厂的各种机器的响声,婴儿啼哭以及喧哗声,凡是刺耳的声音都是噪音,亦称噪声。它对人们的生活、工作影响甚大。噪声使人烦恼、疲劳、紧张和分散注意力。影响人们的学习、工作、休息以及睡眠,严重时引起疾病(如耳聋、心脏病等)和事故。国际上规定90dB为听力保护的最高限度。噪声是目前污染环境的三大公害(污水、废气和噪声)之一,噪声没有污染物,又不会累积,它污染的面积大,其能量最后完全转化为热能而转移。因此,控制噪音是环境保护的一个极为重要的方面。
【超声波】声波频率高于20000Hz,超过一般正常人听觉所能接收到的频率上限,不能引起耳感的声波。其频率通常在2×104~5×108Hz范围之间。它具有与声波一样的传播速度,因为超声波的频率高,波长短,所以它具有很多特性:由于它在液体和固体中的衰减比在空气中衰减小,因而穿透力大;超声波的定向性强,一般声波的波长大,在其传播过程中,极易发生衍射现象,而超声波的波长很短,就不易发生衍射现象,会像光波一样沿直线传播;当超声波遇到杂质会产生反射,若遇到界面时则将产生折射现象;超声波的功率很大,能量容易集中,对物质能产生强大作用,可用来焊接、切削、钻孔、清洗机件等;在工业上被用来探伤、测厚、测定弹性模量等无损检测,以及研究物质的微观结构等;在医学上可用作临床探测,如,用“B超”测肝、胆、脾、肾等病灶,或用来杀菌、治疗、诊断等;在航海、渔业方面,可用来导航、探测鱼群、测量海深等,超声波在各个领域都有广泛的应用。
【次声波】又称亚声波。是低于20Hz,不能引起人的听觉的声波。它传播的速度和声波相同。在很多大自然的变化中,如地震、台风、海啸、火山爆发等过程都会有次声波发生。人为的次声源亦在核爆炸,喷气式机飞行时,以及行驶的车船,压缩机运转时发生。凡晕车、晕船,也都是受车、船运行时次声波的影响。利用次声波亦可监视和检测大气变化。